Tipos y roles de vectores
Los vectores pueden tener diferentes roles según el contexto. Algunos se usan para describir direcciones, otros para indicar una dirección perpendicular o para formar la base de todo un sistema de coordenadas. Aquí vemos los tipos de vectores más importantes.
Vectores de dirección
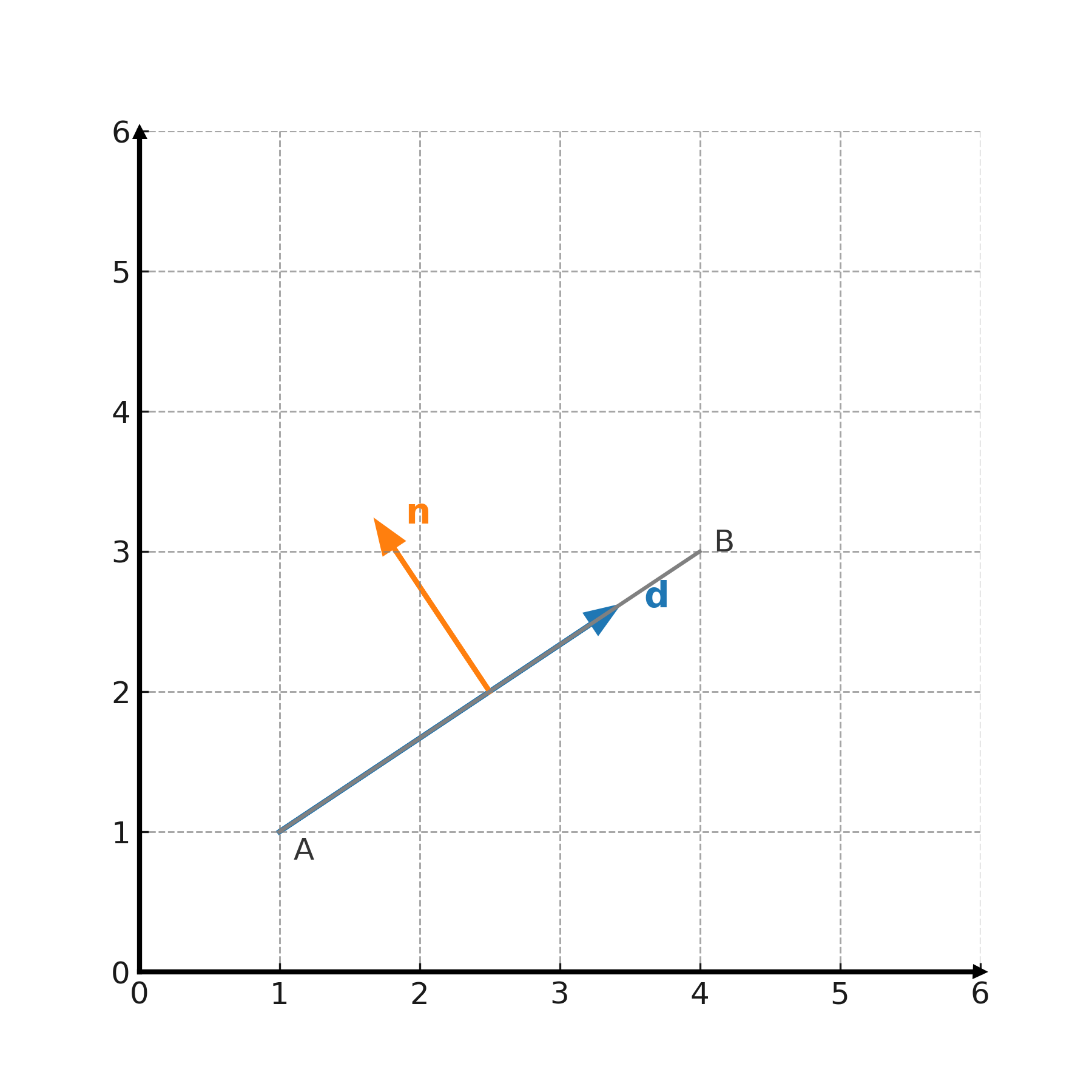
Un vector de dirección (d) describe la dirección de una línea o un plano. Si una línea pasa por los puntos \( \large A=(x_1,y_1) \) y \( \large B=(x_2,y_2) \), entonces
$$ \large \mathbf{d} = (x_2-x_1,\; y_2-y_1) $$
es un vector de dirección de la línea. Con un vector de dirección se puede escribir una representación paramétrica:
$$ \large (x,y) = (x_1,y_1) + t \cdot \mathbf{d}, \quad t \in \mathbb{R} $$
que describe todos los puntos de la línea.
Vectores normales
Un vector normal es perpendicular a una línea o a un plano. Si la línea tiene vector de dirección \( \large (a,b) \), entonces
$$ \large \mathbf{n} = (-b,a) \quad \text{o} \quad (b,-a) $$
son vectores normales. Un vector normal puede usarse para escribir una línea en la forma
$$ \large n_1 \cdot x + n_2 \cdot y + c = 0 $$
donde \( \large (n_1,n_2) \) es el vector normal. Que un vector sea normal puede comprobarse con el producto escalar: Si \( \large \mathbf{r} \cdot \mathbf{n} = 0 \), entonces son perpendiculares.
Vectores unitarios
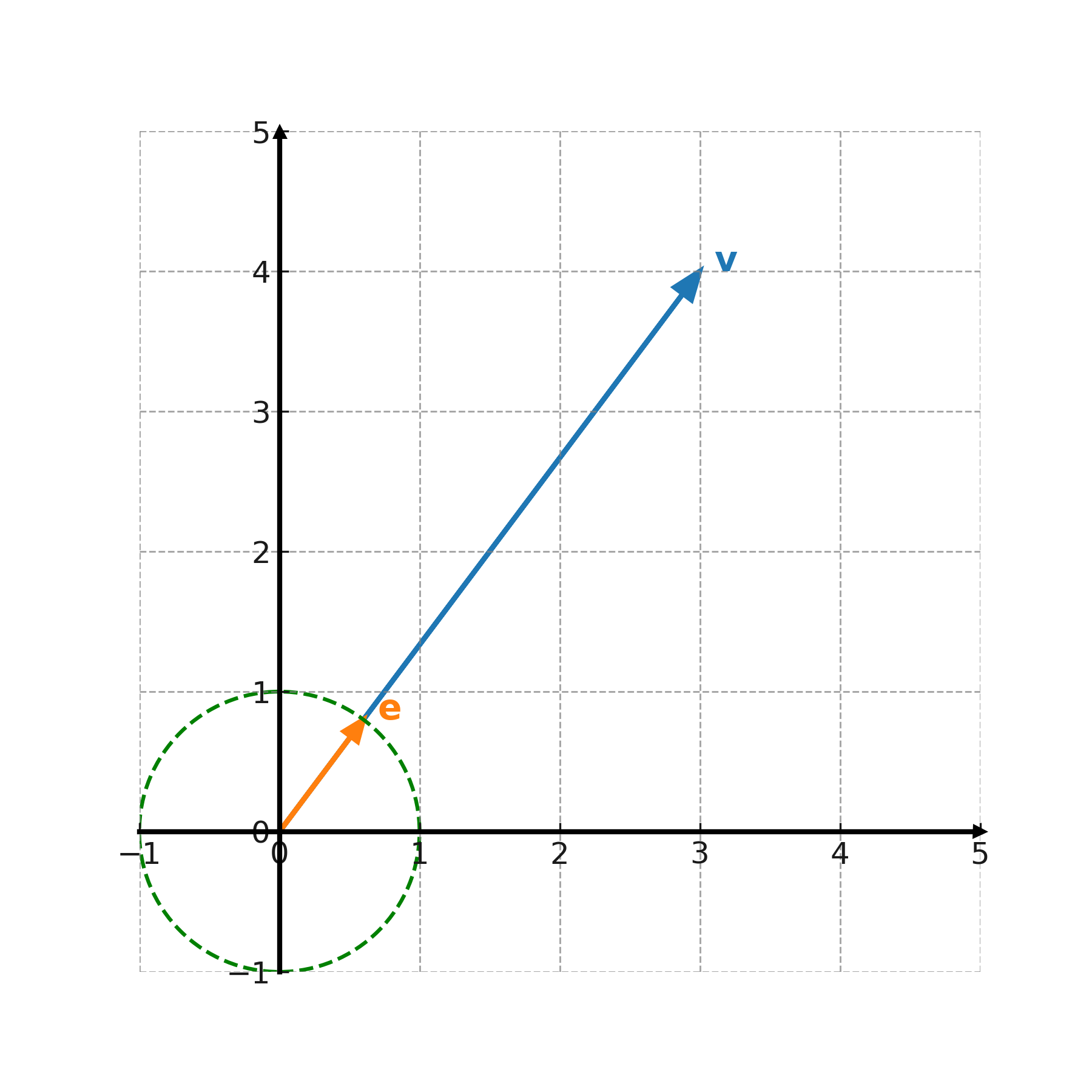
Un vector unitario tiene longitud 1 y se usa para describir una dirección pura. Cualquier vector puede transformarse en vector unitario dividiéndolo por su longitud:
$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$
Los vectores unitarios se usan, por ejemplo, para definir la dirección de los ejes en un sistema de coordenadas.
Vectores tangentes
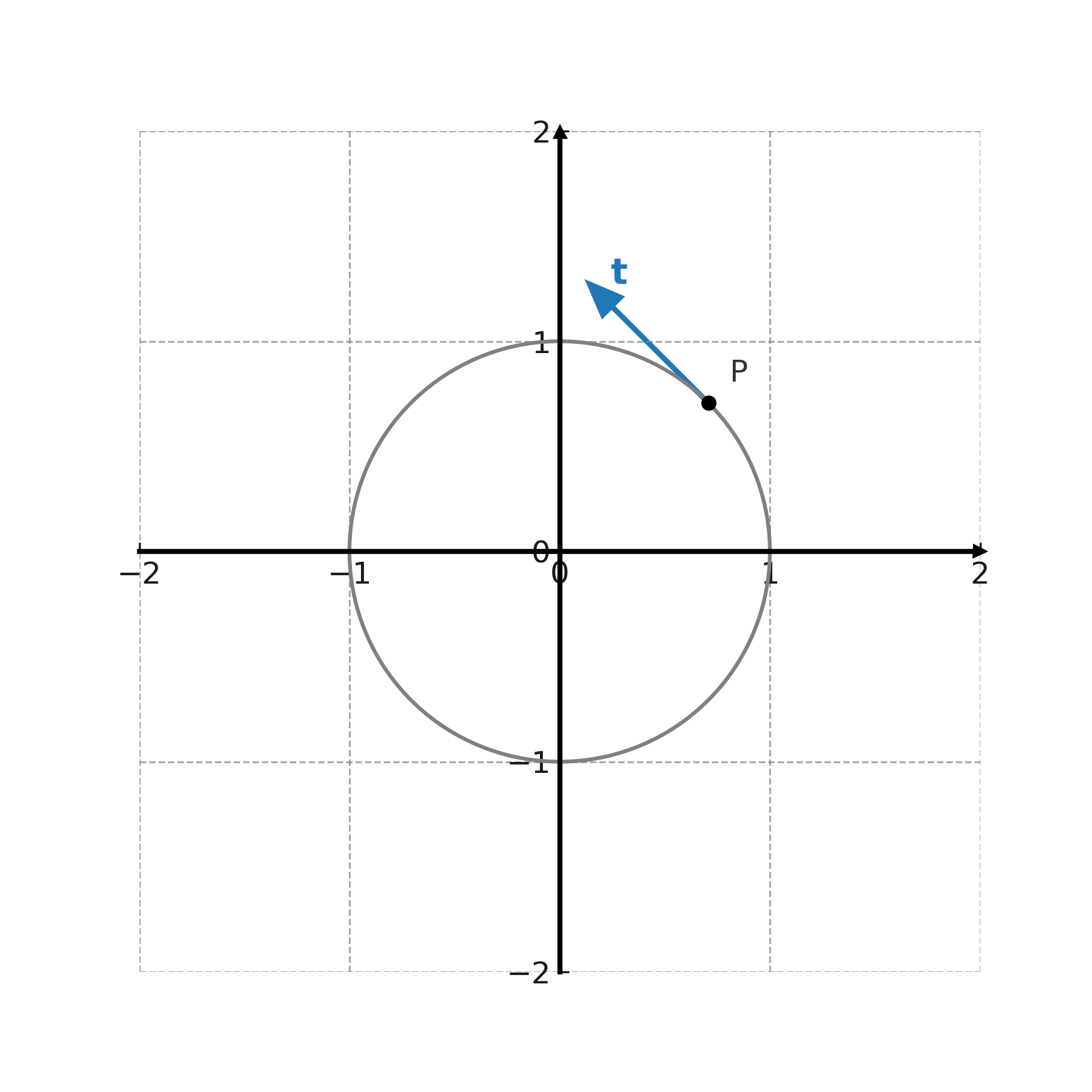
En el contexto de curvas, los vectores tangentes se utilizan para describir la dirección en un punto determinado. Para una curva diferenciable \( \large (x(t),y(t)) \), el vector tangente está dado por
$$ \large \mathbf{t} = \big(x'(t),\,y'(t)\big) $$
que muestra cómo se desplaza la curva en el punto.
Vectores base
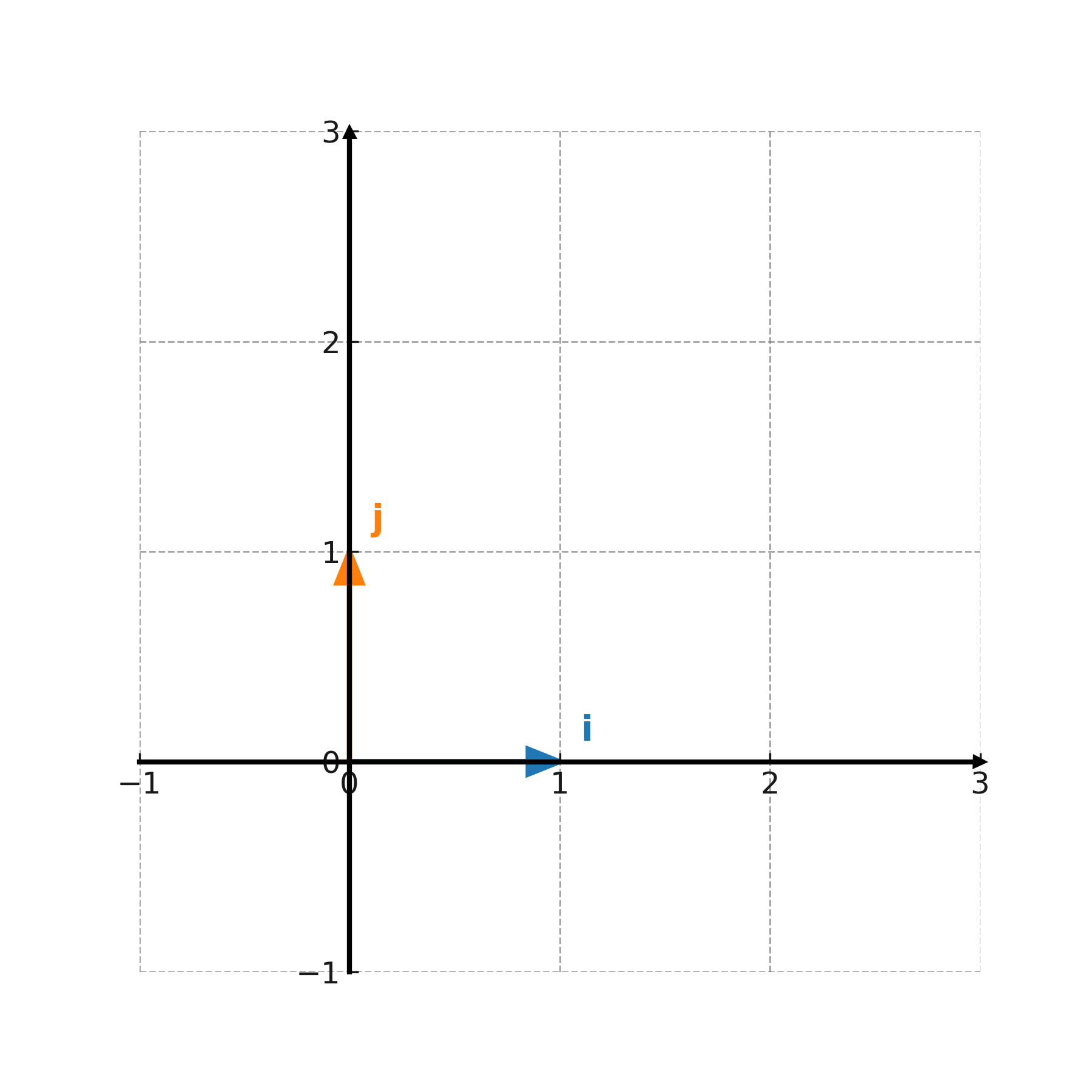
En un sistema de coordenadas se utilizan vectores base para describir todos los demás vectores. En el plano, la base estándar es
$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$
Cada vector puede escribirse como una combinación de estos: \( \large \mathbf{v} = x \cdot \mathbf{i} + y \cdot \mathbf{j} \).
Resumen
Los vectores de dirección se utilizan para indicar direcciones de líneas y planos, los vectores normales para indicar direcciones perpendiculares, los vectores unitarios para aislar la dirección pura, los vectores tangentes para describir el recorrido de las curvas y los vectores base para construir sistemas de coordenadas completos. Juntos forman la base de cómo se aplican los vectores en geometría y álgebra.