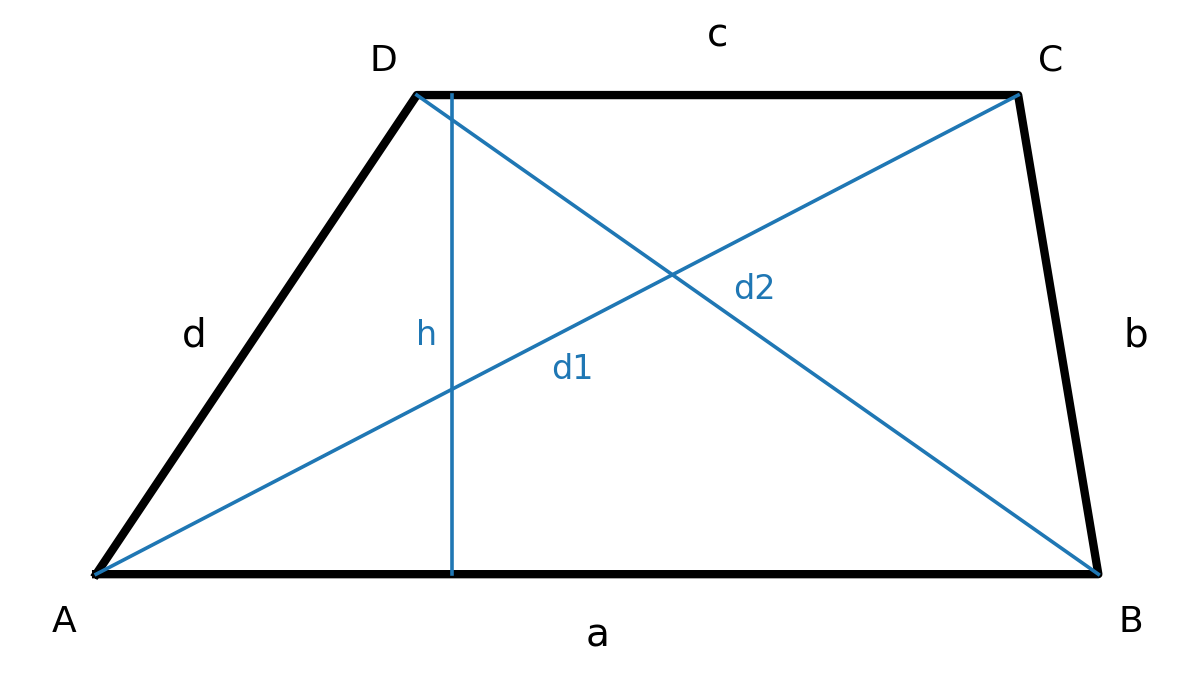
Un trapecio es un cuadrilátero donde dos de los lados son paralelos. Los lados paralelos se llaman bases.

Si los otros dos lados también son paralelos, la figura es un paralelogramo. Los lados que no son paralelos se llaman piernas.

Variantes

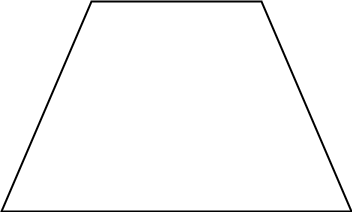
Trapecio isósceles: \(b=d\). Los ángulos de la base en cada base son iguales por pares y las diagonales tienen la misma longitud.

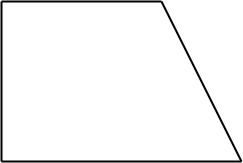
Trapecio rectángulo: Dos de los ángulos son rectos.

Propiedades

• La suma de los ángulos interiores es 360°.
• A lo largo de cada pierna, \( \angle A + \angle D = 180^\circ \) y \( \angle B + \angle C = 180^\circ \) (paralelismo).
• El segmento medio (la línea que une los puntos medios de las piernas) tiene la longitud \( m=\tfrac{a+c}{2} \), y el área se puede escribir como \( A=m\cdot h \).

Área y perímetro

La fórmula estándar para el área:

$$ \large A=\tfrac{h}{2}\,(a+c) $$

Si se conocen los ángulos de la base en \(A\) y \(B\), las longitudes de las piernas se pueden escribir como \( d=\tfrac{h}{\sin(\angle A)} \) y \( b=\tfrac{h}{\sin(\angle B)} \). Así el perímetro es:

$$ \large P = (a+c) + h\!\left(\tfrac{1}{\sin(\angle A)}+\tfrac{1}{\sin(\angle B)}\right) $$

Área a partir de cuatro lados

Si se conocen los cuatro lados, la altura y por lo tanto el área se pueden encontrar sin ángulos:

$$ \large A = \tfrac{1}{2}(a+c)\,\sqrt{\,b^2 - \Bigl(\tfrac{(a-c)^2 + b^2 - d^2}{2(a-c)}\Bigr)^2} $$

Aquí se supone que \(a \ne c\). Para un paralelogramo se toma el límite \(a \to c\).

Diagonales

Las diagonales se obtienen con la ley de cosenos en los triángulos correspondientes:

$$ \large d_1 = \sqrt{a^2 + b^2 - 2ab\cos(\angle B)} $$

$$ \large d_1 = \sqrt{c^2 + d^2 - 2cd\cos(\angle D)} $$

$$ \large d_2 = \sqrt{a^2 + d^2 - 2ad\cos(\angle A)} $$

$$ \large d_2 = \sqrt{b^2 + c^2 - 2bc\cos(\angle C)} $$

En un trapecio isósceles se cumple \(d_1=d_2\).

Circunferencia circunscrita

Solo los trapecios isósceles se pueden inscribir en un círculo. Equivalentemente, se cumplen las sumas de ángulos opuestos:

• \(\angle A + \angle C = 180^\circ\)
• \(\angle B + \angle D = 180^\circ\)

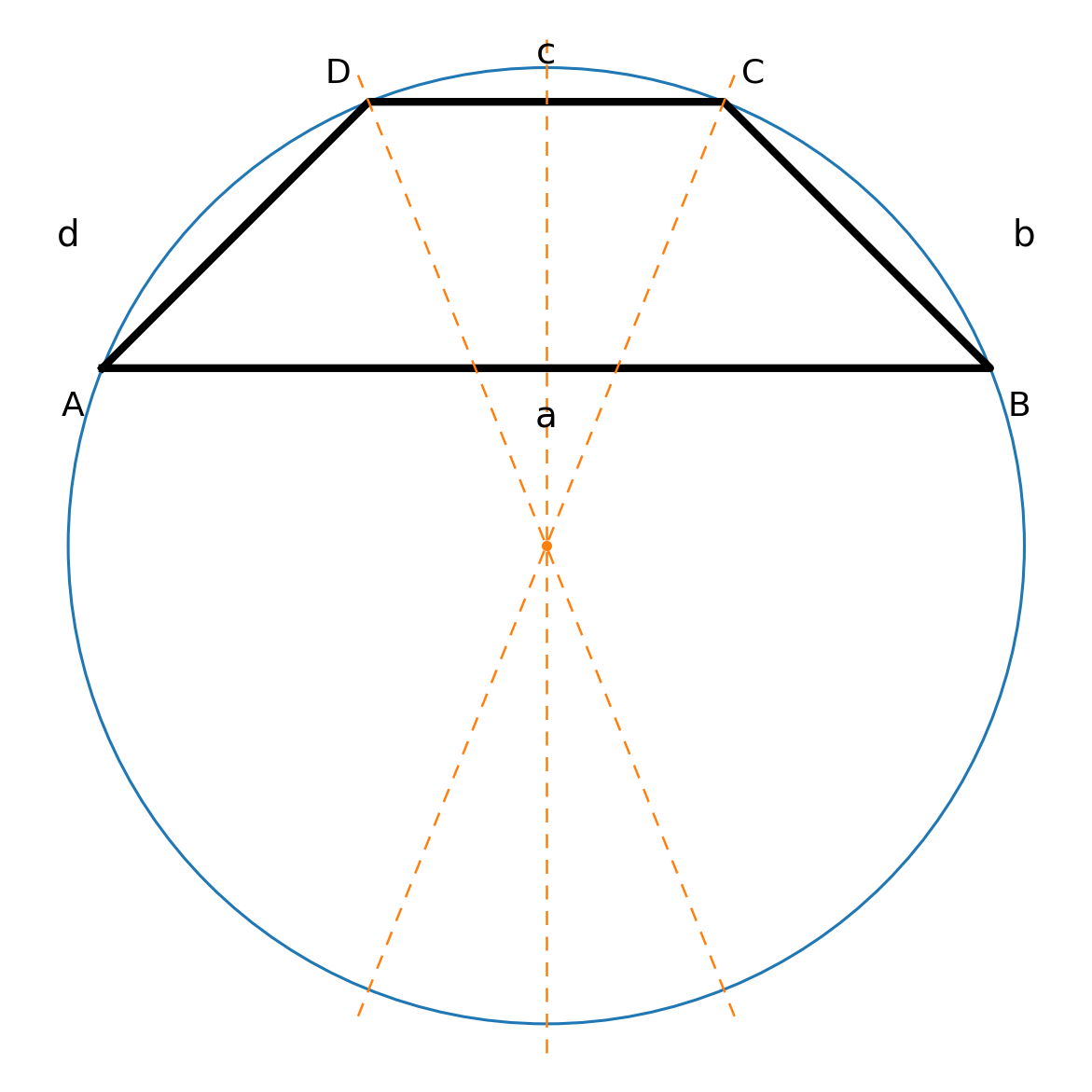
El centro del círculo se puede encontrar dibujando bisectrices de ángulo desde C y D, y opcionalmente también la mediatriz de los lados a y c (el eje de simetría).

Obsérvese que para cualquier trapecio se cumple que \( \angle A + \angle D = 180^\circ \) y \( \angle B + \angle C = 180^\circ \) como consecuencia de las líneas paralelas. Eso por sí solo no lo hace cíclico.

Circunferencia inscrita

Un trapecio tiene una circunferencia inscrita, tangente a los cuatro lados, si y solo si:

$$ \large a + c = b + d $$

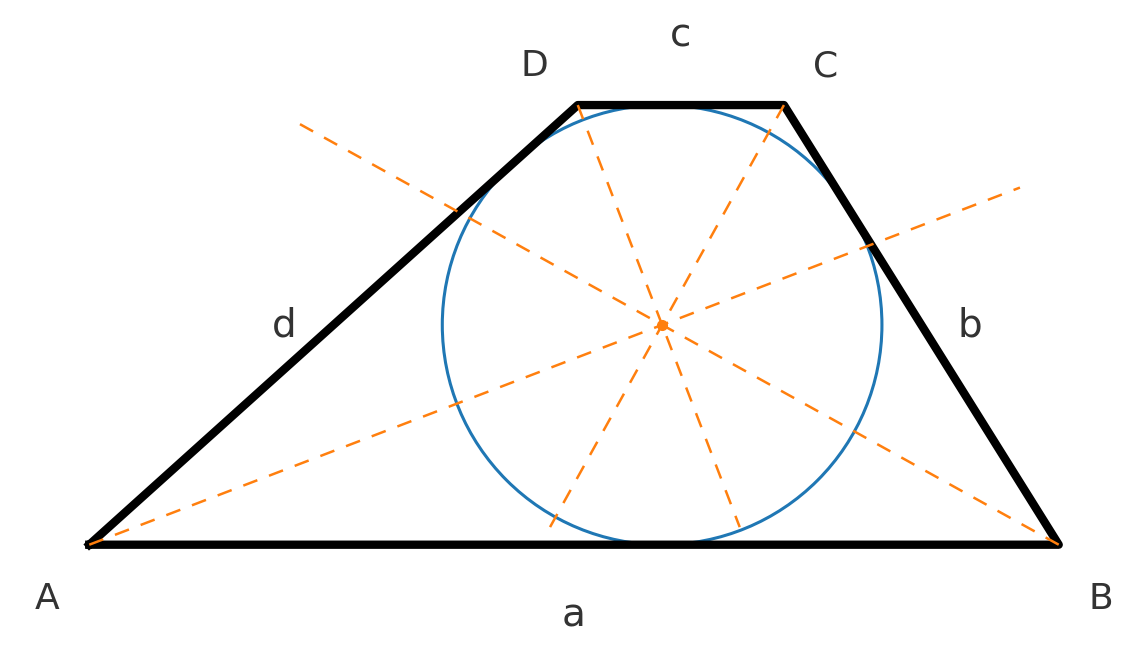
El centro del círculo se puede encontrar dibujando bisectrices de ángulo desde los cuatro ángulos.

Para los cuadriláteros tangenciales también se cumple \( A = r \cdot s \), donde \( r \) es el inradio y \( s \) es el semiperímetro.

Aplicaciones

• Dividir en dos triángulos rectángulos más un rectángulo hace que las construcciones y cálculos trigonométricos sean manejables.
• La regla del trapecio se utiliza para la aproximación numérica de integrales.