Paralelogramo
Un paralelogramo es un cuadrilátero en el que los lados opuestos son de igual longitud y paralelos.
La figura puede verse como un "rectángulo inclinado".
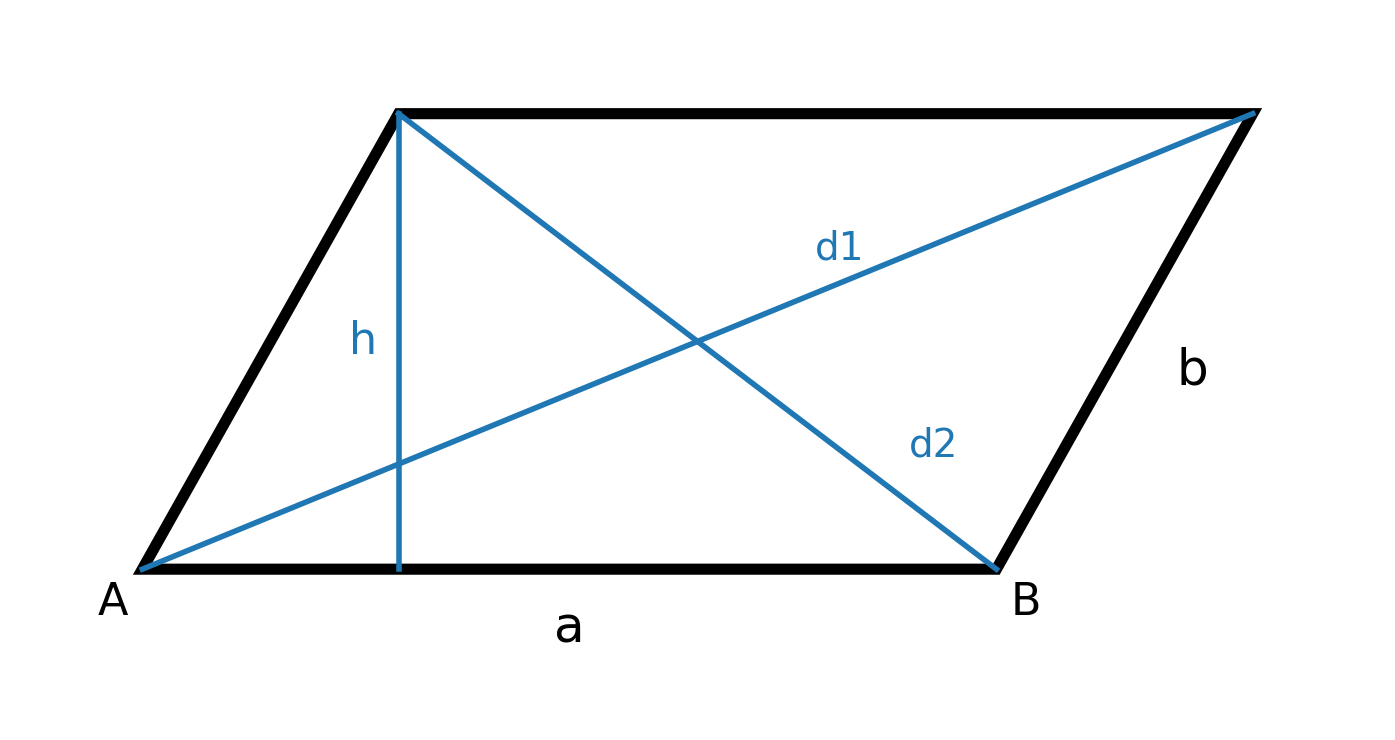
No hay ángulos rectos en un paralelogramo, pero los ángulos opuestos siempre son iguales. La suma de dos ángulos adyacentes es 180°.
$$ \large \angle A + \angle B = 180^\circ $$
Una variación especial del paralelogramo se llama rombo. Aquí los cuatro lados son de igual longitud. De la misma manera que un rectángulo equilátero se llama cuadrado.
El punto de intersección de las diagonales en un paralelogramo es también su punto medio.
Esto significa que las diagonales se dividen mutuamente en dos partes iguales, pero no son necesariamente perpendiculares.
Propiedades de un paralelogramo
- Los lados opuestos son de igual longitud.
- Los lados opuestos son paralelos.
- Los ángulos opuestos son iguales.
- Los ángulos adyacentes suman 180°.
- El punto de intersección de las diagonales es también su punto medio.
- Un paralelogramo puede dividirse en dos triángulos congruentes a lo largo de una diagonal.
Al calcular con un paralelogramo, a menudo es necesario usar trigonometría y cálculos con triángulos.