Rombo
Un rombo es un cuadrado inclinado y se parece mucho a un paralelogramo, que es un rectángulo inclinado.
También se puede decir que todos los cuadrados son rombos, pero no todos los rombos son cuadrados, porque los ángulos de un rombo no tienen por qué ser de 90 grados.
El rombo suele ser fácil de calcular en la práctica, porque todos sus lados son iguales en longitud, igual que en un cuadrado.
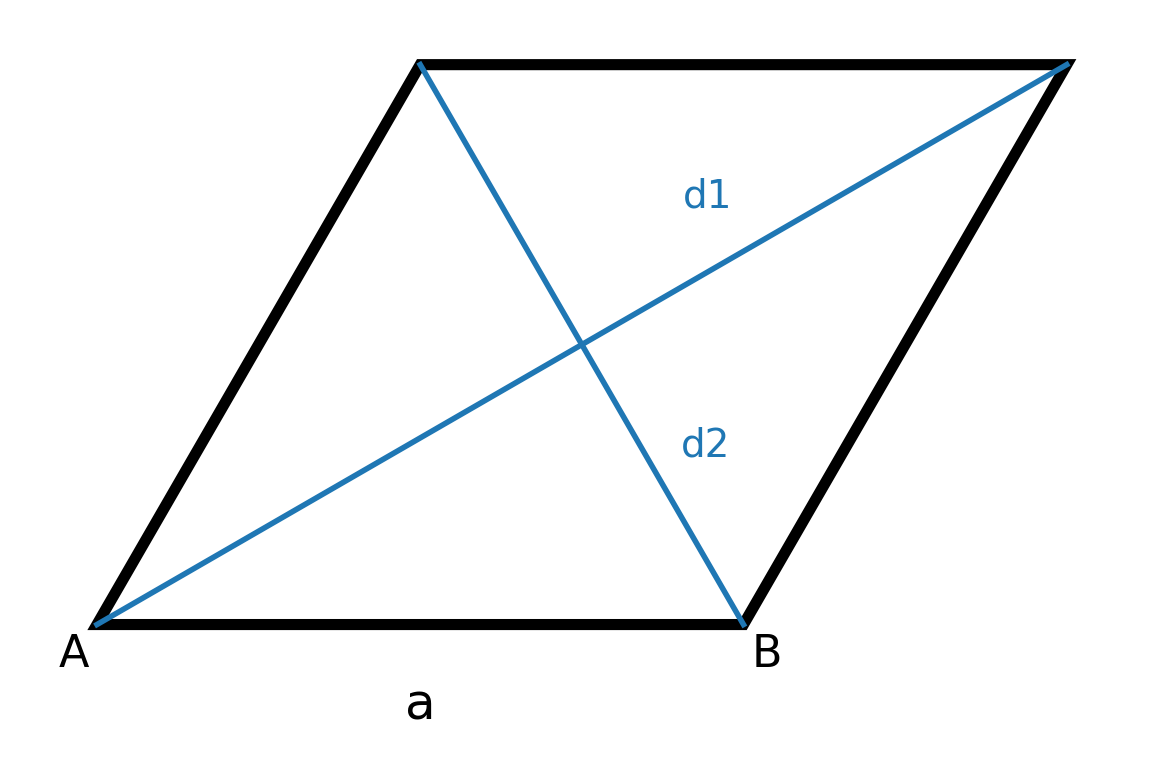
Propiedades que caracterizan a un rombo
- Los cuatro lados son de igual longitud.
- Los lados opuestos son paralelos.
- Los ángulos opuestos son iguales y los ángulos adyacentes suman 180 grados.
- El punto de intersección de las diagonales es también su punto medio.
- Las diagonales son perpendiculares entre sí.
- Cada diagonal biseca los ángulos adyacentes, por lo que la figura tiene dos ejes de simetría a lo largo de las diagonales.
- El rombo puede dividirse en cuatro triángulos rectángulos congruentes.
El hecho de que las diagonales se bisecan y sean perpendiculares significa que el rombo puede dividirse en triángulos rectángulos.
Esto permite utilizar el teorema de Pitágoras y la trigonometría elemental en los cálculos.