The Poisson distribution is a probability distribution that describes the probability of a certain number of events in a given time period or area, when the events occur independently of each other and with a constant average rate. It is often used to model rare events.

Definition

A random variable \(\large X\) is said to follow a Poisson distribution with parameter \(\large \lambda\) if it has the probability function:

$$ \large P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}, \quad k = 0, 1, 2, \dots $$

Here \(\large \lambda\) is the average number of events in the time period or area.

Properties

• Mean: \( E(X) = \lambda \)
• Variance: \( Var(X) = \lambda \)
• Only one parameter \(\lambda\), which determines both mean and spread
• Discrete distribution (defined for \(k = 0,1,2, \dots\))

Example

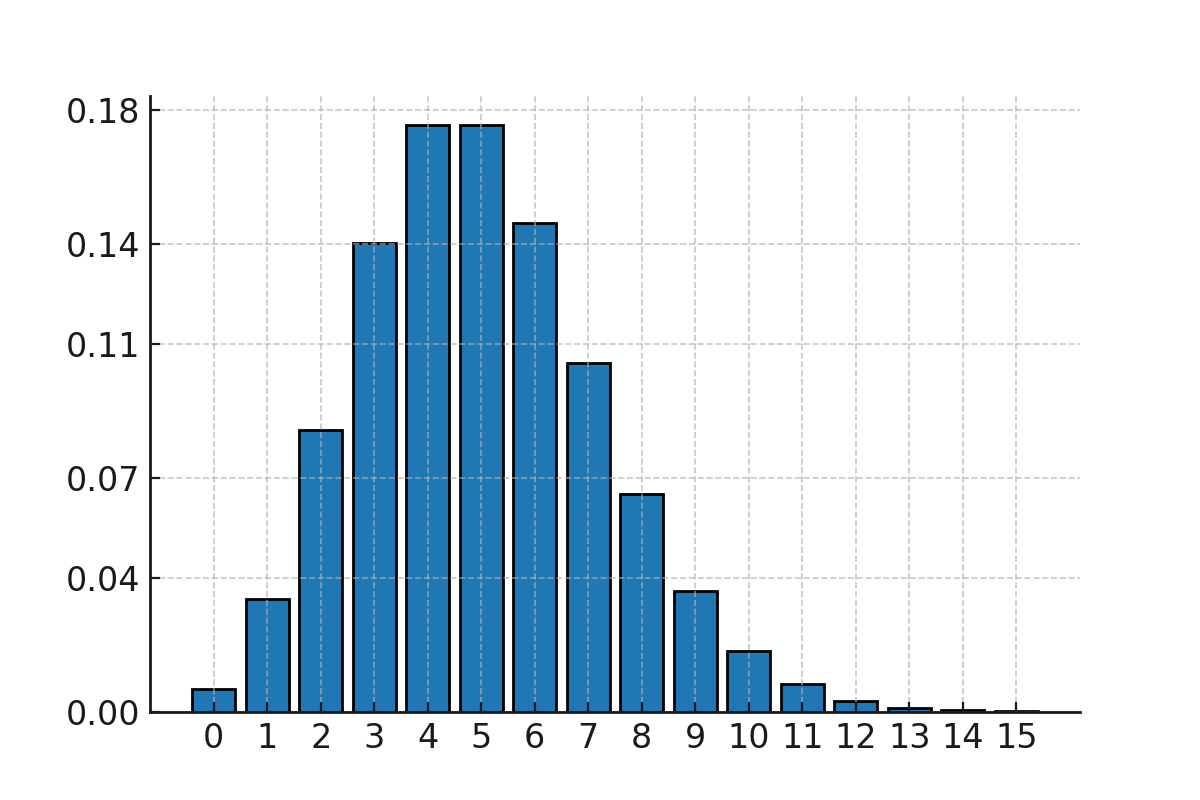
Assume that the number of emails a person receives in one hour follows a Poisson distribution with \(\large \lambda = 5\).

What is the probability of receiving exactly 3 emails in one hour?

$$ \large P(X = 3) = \frac{5^3 \cdot e^{-5}}{3!} $$

$$ \large P(X = 3) = \frac{125 \cdot e^{-5}}{6} $$

$$ \large P(X = 3) \approx 0.1404 $$

Thus, there is about a 14% probability of receiving exactly 3 emails in one hour.

Graph

The Poisson distribution can be shown as a bar chart, where the probability for each possible outcome \(\large k\) is drawn. The distribution is typically skewed, but becomes more symmetric as \(\large \lambda\) increases.

Relation to the binomial distribution

The Poisson distribution can be seen as an approximation to the binomial distribution. If the number of trials \(\large n\) is very large and the probability of success \(\large p\) is very small, the binomial distribution \( B(n,p) \) can be approximated by a Poisson distribution with parameter:

$$ \large \lambda = n \cdot p $$

This relationship makes the Poisson distribution particularly useful in situations with rare events, where the binomial distribution would be heavy to compute.