Law of Large Numbers

Store tals lov er et grundlæggende princip i sandsynlighedsregning.

Den siger, at jo flere gange man gentager et forsøg, desto tættere vil de observerede resultater ligge på den teoretiske sandsynlighed.

 

 

Eksempel med terning

Hvis man kaster en terning én gang, er der ingen garanti for at slå en sekser.

Kaster man den 6 gange, kan det sagtens ske, at der slet ikke kommer nogen sekser.

Kaster man den 1.000 gange, vil man typisk opleve, at ca. en sjettedel af kastene giver sekser – altså omkring 167 gange.

 

 

Teoretisk sandsynlighed

Vi ved, at sandsynligheden for at slå en sekser er:

 

$$ P(\text{sekser}) = \tfrac{1}{6} \approx 0,167 = 16,7\% $$

 

Statistisk sandsynlighed

I et eksperiment med 1.000 kast får vi måske resultatet:

 

• Antal seksere: 158
• Statistisk sandsynlighed: \( \tfrac{158}{1000} = 0,158 = 15,8\% \)

 

Det ligger tæt på den teoretiske værdi på 16,7 %. 

 

 

 

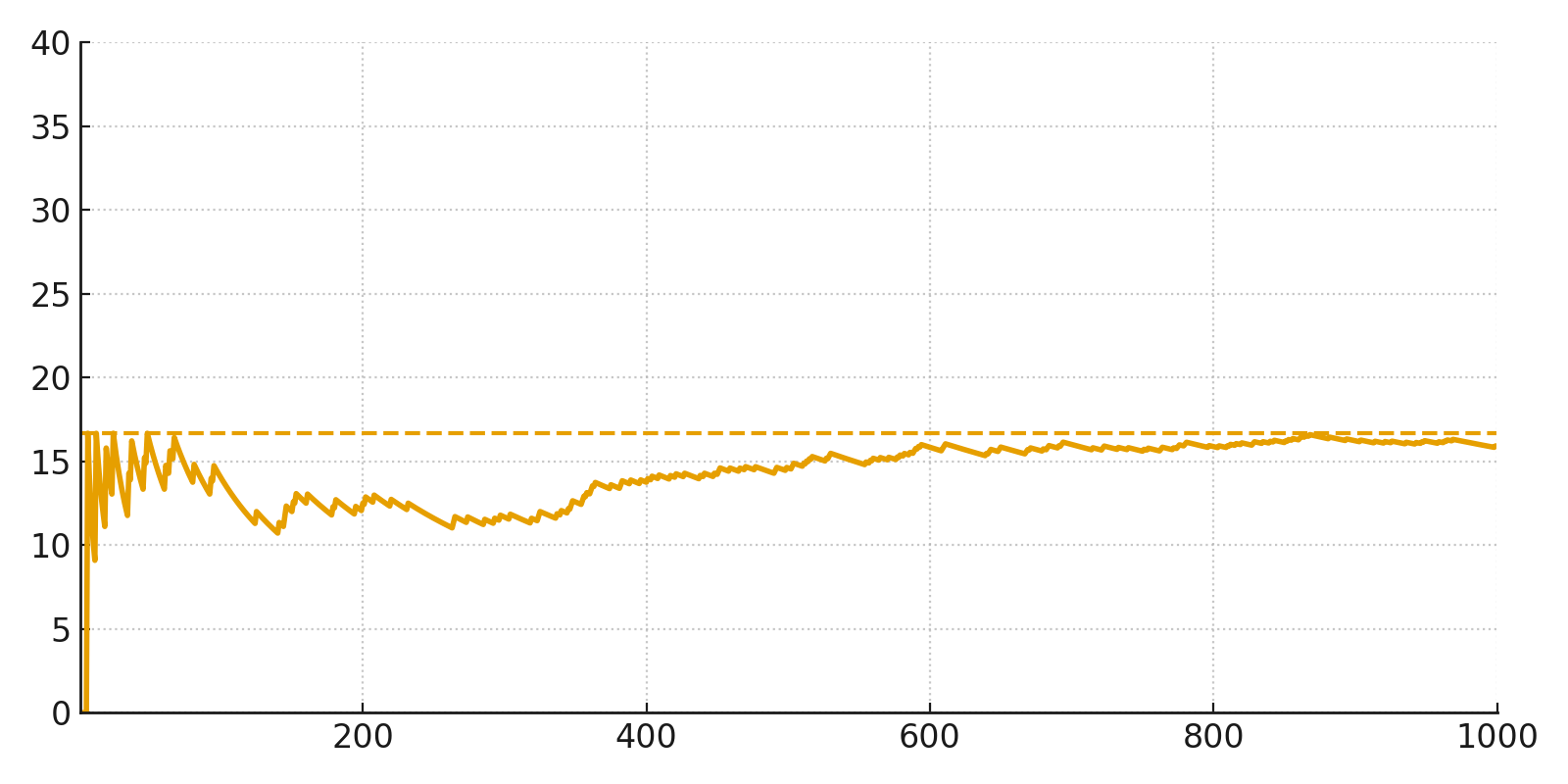
Her har vi kastet en terning 1.000 gange og fulgt med i, hvor stor en procentdel af kastene der gav en sekser.

I starten svinger kurven meget, men efterhånden som antallet af kast vokser, stabiliserer den sig omkring den teoretiske sandsynlighed på ca. 16,7 %.

Det er præcis det, Store tals lov handler om: at sandsynligheder først giver mening, når vi har mange observationer.

 

 

Betydning

Store tals lov viser, hvorfor sandsynligheder giver mening i praksis:

 

• Små datasæt kan give tilfældige udsving.
• Store datasæt giver et mere pålideligt billede.

 

 

Sammenfatning

• Store tals lov gælder for mange gentagelser af et forsøg.
• De empiriske frekvenser nærmer sig de teoretiske sandsynligheder.
• Jo større stikprøve, desto mere præcist resultat.