Law of sines
The law of sines can be used in cases where one knows an angle-side pair, that is, where one of the known sides lies opposite the known angle.
Thus, if you know angle \(A\) and the sides \(a\) and \(b\), you should use the law of sines.
An arbitrary triangle is neither right-angled, equilateral, nor isosceles.
The law of sines is expressed as follows:
$$ {a \over \sin(A)} = {b \over \sin(B)} = {c \over \sin(C)} $$
So if you know angle \(A\) and the sides \(a\) and \(b\), and you need to find angle \(B\), you use the following and isolate angle \(B\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] \sin(B) = {b \cdot \sin(A) \over a} $$
The result will be a number between 0 and 1, for example 0.866. To find the angle you must use \( \sin^{-1} \) on your calculator:
$$ \sin^{-1}(0,866) = 60^\circ $$
The angle is therefore 60 degrees.
If you know two angles and only one side, you can also use the law of sines. Let us assume that you know angles \(A\) and \(B\), as well as side \(a\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] b = {a \cdot \sin(B) \over \sin(A)} $$
Note: If the calculation gives \(\sin(v) > 1\), there is no solution. This means that the given triangle cannot exist with the information you have.
Sine and obtuse triangles
If you calculate angles with sine in a triangle that turns out to be obtuse, you must be careful, because there can be two results depending on how much you know about the triangle.
Let us assume that you have the following information about a triangle:
- Angle A = 25 degrees
- Side a = 3
- Side c = 5
With this information we can calculate angle \(C\):
$$ \begin{align}{a \over \sin(A)} &= {c \over \sin(C)} \Leftrightarrow \\[10pt] \sin(C) &= {c \cdot \sin(A) \over a } \Leftrightarrow \\[10pt] \sin(C) &= {5 \cdot \sin(25^\circ) \over 3 } \Leftrightarrow \\[10pt] \sin(C) &= 0,704 \Leftrightarrow \\[10pt] \sin^{-1}(0,704) &= 44,78^\circ \end{align} $$
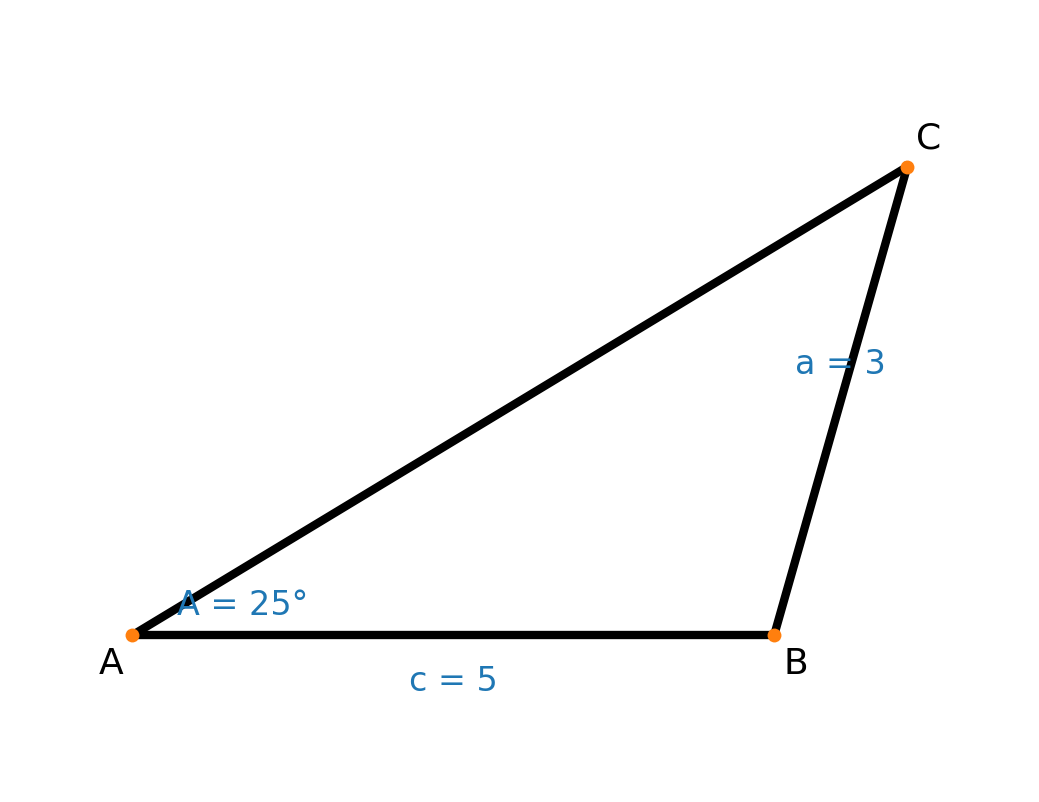
The result is therefore a triangle, as shown above, with:
- Angle A = 25°
- Angle B = 110,22°
- Angle C = 44,78°
Calculation of the obtuse angle
If you look at the figure below, you can see that it is possible to draw another triangle with the same information.
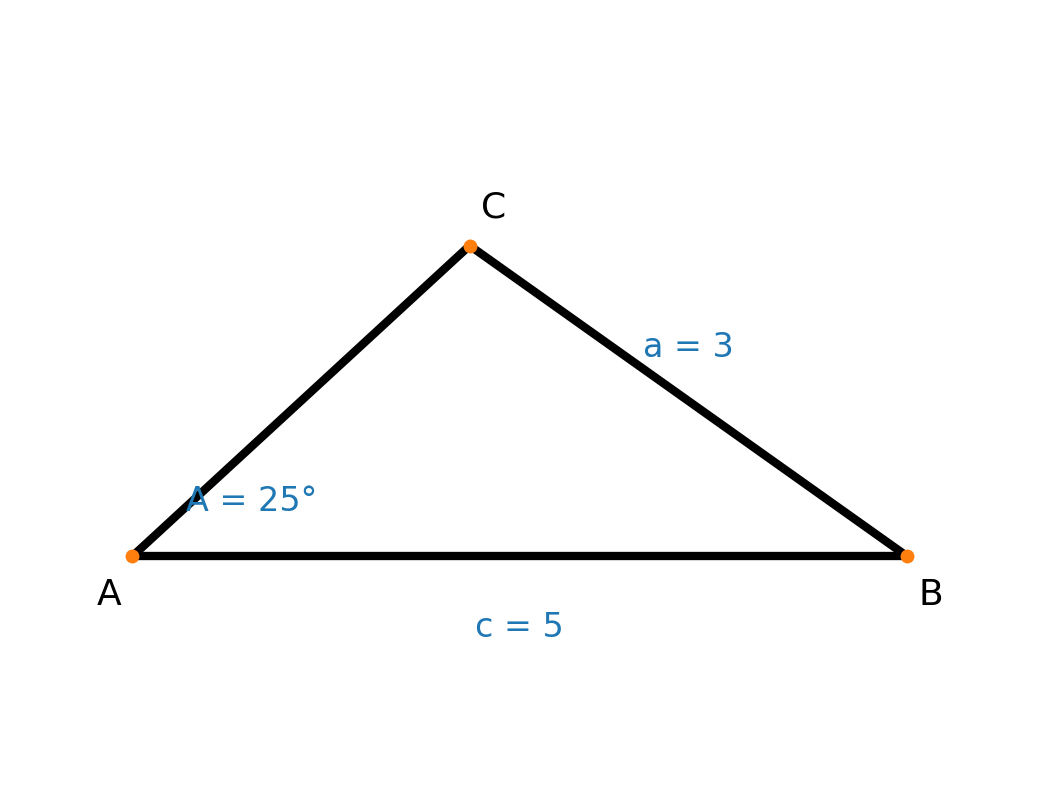
The law of sines always returns the acute solution (between 0° and 90°). The possible obtuse solution is found by subtracting the acute angle from 180°.
We assume that the acute angle is 44.78°, as calculated earlier, and call it \(C_1\). The obtuse angle we call \(C_2\):
$$ C_2 = 180 - C_1 \Leftrightarrow \\[12pt] C_2 = 135,22^\circ $$
Now you know angle \(C\) for both triangles and can calculate the rest for both. This means that side \(b\) also has two different lengths (the same applies to perimeter, height and area).
Therefore you must always check whether the found solution can have an obtuse angle when using the law of sines.
The rule for when there are two solutions is: If the angle you calculate with the law of sines is less than 90 degrees, there will be two results.