Double- and half-angle formulas

In trigonometry, double and half angle formulas describe how sine, cosine, and tangent can be expressed when the angle is doubled or halved.

The formulas are derived directly from the addition and subtraction formulas and make it possible to find new connections between the trigonometric functions.

 

Double angle formulas

By setting \( \alpha = \beta \) in the addition formulas, we get:

 

$$ \large \sin(2v) = 2 \sin(v) \cdot \cos(v) $$

$$ \large \cos(2v) = \cos^2(v) - \sin^2(v) $$

$$ \large \tan(2v) = \frac{2 \tan(v)}{1 - \tan^2(v)} $$

 

 

 

The cosine formula can also be rewritten into other useful forms by using the Pythagorean identity:

 

$$ \large \cos(2v) = 2\cos^2(v) - 1 = 1 - 2\sin^2(v) $$

 

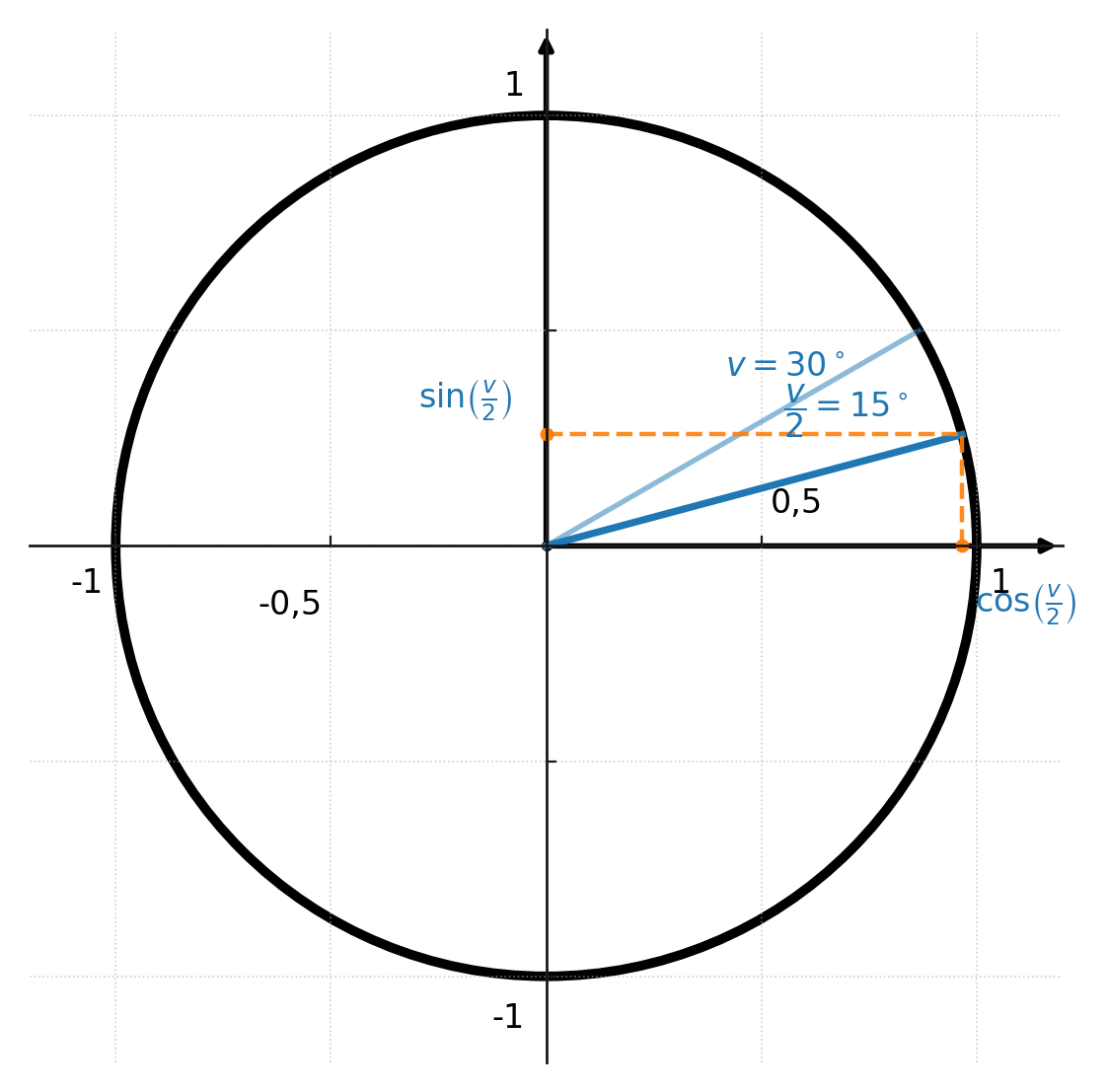
Half angle formulas

The half angle formulas are obtained by isolating \(\sin v\) and \(\cos v\) in the double angle formulas. The result is:

 

$$ \large \sin\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 - \cos(v)}{2}} $$

$$ \large \cos\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 + \cos(v)}{2}} $$

$$ \large \tan\!\left(\tfrac{v}{2}\right) = \tfrac{\sin(v)}{1 + \cos(v)} = \tfrac{1 - \cos(v)}{\sin(v)} $$

 

The signs \(+\) or \(-\) depend on which quadrant the angle is in.

 

 

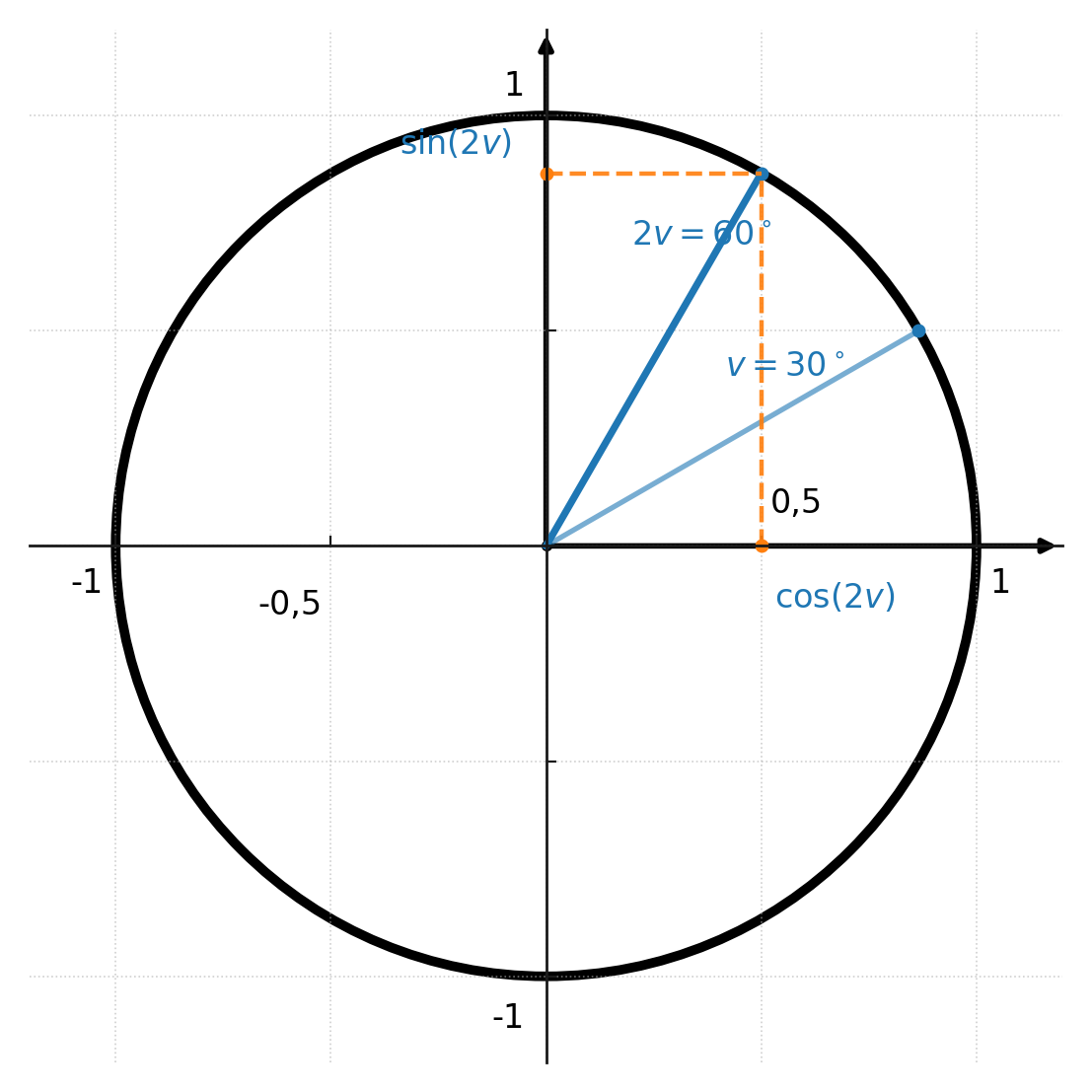
Example

We want to calculate \( \sin(2 \cdot 30^\circ) \):

 

$$ \large \sin(60^\circ) = 2 \cdot \sin(30^\circ) \cdot \cos(30^\circ) $$

$$ \large = 2 \cdot \tfrac{1}{2} \cdot \tfrac{\sqrt{3}}{2} = \tfrac{\sqrt{3}}{2} $$

 

Application

• The formulas are used to find exact values for angles such as 15°, 22.5°, and 75°.
• They are useful in proofs and trigonometric transformations.
• The half angle formulas are often used to solve trigonometric equations.