Relations

In trigonometry, relations are the formulas and connections that link the trigonometric functions together. While the functions (sine, cosine, tangent, etc.) each describe a specific ratio, the relations show how the functions are connected and can be used to calculate sides and angles in triangles.

 

Pythagorean Identity

One of the most fundamental relations is the Pythagorean identity, which shows the connection between sine and cosine for any angle:

 

$$ \sin^2(v) + \cos^2(v) = 1 $$

 

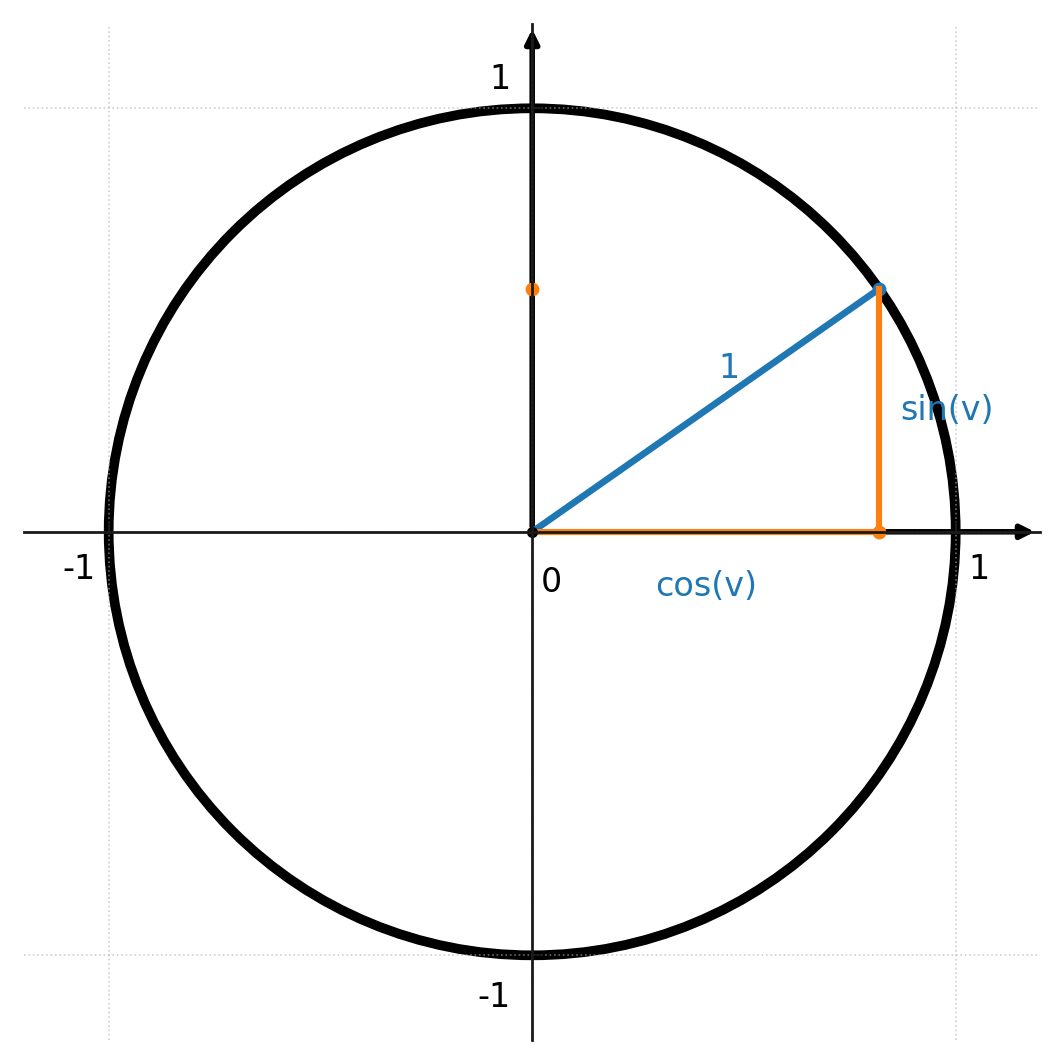
The identity follows directly from the unit circle.

If a point on the circle has the coordinates \( (\cos v, \sin v) \), Pythagoras’ theorem applies, because the radius is always 1:

 

$$ (\cos v)^2 + (\sin v)^2 = 1^2 = 1 $$

 

 

Application

The Pythagorean identity makes it possible to calculate sine if cosine is known, or cosine if sine is known.

It is also the foundation for many other trigonometric identities.

 

Example: If \( \cos v = 0.6 \), sine can be found as follows:

 

$$ \sin^2(v) = 1 - \cos^2(v) = 1 - 0.6^2 = 0.64 $$

$$ \sin(v) = \pm \sqrt{0.64} = \pm 0.8 $$

 

Note that there are two solutions, because the angle can lie in both the first and the second quadrant.

 

The Pythagorean identity is the most fundamental trigonometric relation and forms the basis for many other formulas and calculations in trigonometry.