A circular segment is a part of a circle bounded by a chord and the corresponding arc. The shape can resemble a half-arch.

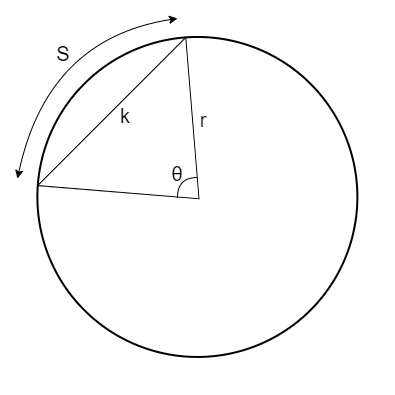
A circular segment is described by the radius r, the angle \(\large \theta\), the chord c, the arc length S, and the height h. One can also calculate the area of the segment, which is always a part of the circle’s total area.

Angle in degrees and radians

To work with circular segments, the angle is often expressed in radians. A full circle corresponds to \(360^\circ\) or \(2\pi\) radians.

There are simple formulas to convert between degrees and radians, and it is important to choose the correct one depending on the angle unit used.

$$ \large \theta = \frac{v_{deg} \cdot \pi}{180} $$

$$ \large v_{deg} = \frac{\theta \cdot 180}{\pi} $$

From sector to segment

A circular segment can also be understood as the difference between a circular sector and the triangle formed by the two radii and the chord. In this way, the area of the segment can be seen as part of a sector’s area.

For example, a segment with an angle of \(60^\circ\) can be calculated by finding the area of the sector and subtracting the area of the triangle.

Example

A circle has radius \(r = 10 \,\text{cm}\), and we consider a circular segment with an angle of \(60^\circ\).

First, convert the angle to radians:

$$ \large \theta = \frac{60 \cdot \pi}{180} $$

$$ \large \theta = \frac{\pi}{3} \approx 1.047 \,\text{rad} $$

The area of the circular sector is found first, and then the area of the triangle is subtracted to obtain the area of the segment:

$$ \large A = \frac{1}{2} r^2 \theta - \frac{1}{2} r^2 \sin(\theta) $$

Inserting \(r=10\) and \(\theta = \frac{\pi}{3}\):

$$ \large A = \frac{1}{2} \cdot 100 \cdot \frac{\pi}{3} - \frac{1}{2} \cdot 100 \cdot \sin\!\left(\frac{\pi}{3}\right) $$

$$ \large A \approx 9,059 \,\text{cm}^2 $$

Summary

A circular segment is therefore a part of a circle defined by a chord and its corresponding arc.

It can be described by the radius, chord, height, and angle, and its area is found as the difference between the circular sector and the triangle.