A circle is the set of points that are all the same distance from a given point.

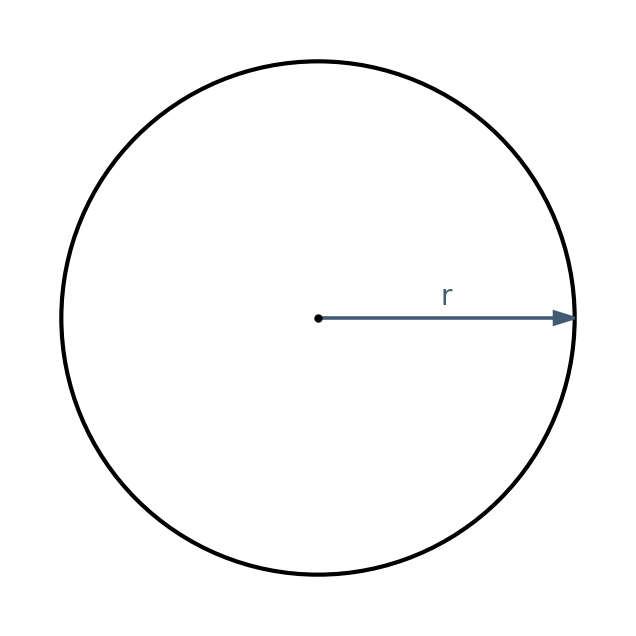
The given point is called the center, and the distance to the edge of the circle is called the radius. The diameter is twice the radius and passes through the center.

The circle is one of the fundamental figures in mathematics and geometry, and many formulas are connected to it. The most important ones are related to the number Pi (\(\large \pi\)).

Pi (\(\pi\))

When working with circles, you always encounter the number Pi (\(\large \pi\)).

Pi describes the ratio between a circle’s circumference and its diameter. No matter the size of the circle, it holds that:

$$ \large \pi = \frac{\text{circumference}}{\text{diameter}} $$

The value of Pi is about 3.14. But Pi is an infinite, non-repeating decimal, and it cannot be written exactly as a fraction. It begins like this:

3.141592653589793...

A famous fraction that comes very close to Pi is:

$$ \large \frac{355}{113} \approx 3.1415929 $$

This matches Pi to six decimal places, but it is still only an approximation.

Today, computers have calculated billions of decimals of Pi. For everyday use it is enough to use 3.14, but if your calculator has a \(\large \pi\) button, you should use it, as it is more precise.

The circle in practice

Imagine a wheel with a diameter of 1 meter. When it rolls one full turn, it has moved about 3.14 meters. If we use a more precise value of Pi, the result will be slightly longer – but the principle is the same.

The circle has both circumference and area. These can be calculated directly from the radius or diameter and the number Pi. For example, if the diameter is 10 cm, then the radius is 5 cm.

We can then find:

$$ \large Area = r^2 \cdot \pi \quad \Leftrightarrow \quad A= 78.5 \text{ cm}^2 $$

$$ \large Circumference = 2 \cdot r \cdot \pi \quad \Leftrightarrow \quad C= 31.4 \text{ cm} $$

A circle has the same area as a right triangle where one leg is the circle’s radius and the other leg is the circle’s circumference. This is a beautiful connection that shows how deeply Pi is embedded in geometry.

Pi as a fraction

Even though Pi cannot be written as an exact fraction, you can find fractions that come very close.

These are called fraction approximations, and the best come from a method called continued fractions. This is a way to write a number as a chain of integer divisions.

For example, Pi can be written as:

$$ \large \pi = 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \cfrac{1}{292 + \cdots}}}} $$

If you stop this expansion after a few steps, you get fractions called convergents. They provide the best possible approximations for denominators that small.

Some of the most famous approximations are:

$$ \large \frac{22}{7} \approx 3.142857 $$

$$ \large \frac{333}{106} \approx 3.141509 $$

$$ \large \frac{355}{113} \approx 3.1415929 $$

$$ \large \frac{103993}{33102} \approx 3.1415926530 $$

$$ \large \frac{104348}{33215} \approx 3.1415926539 $$

Each new fraction is closer to Pi than the previous one. That is why fractions such as 355/113 and 104348/33215 became famous – they hit Pi with a precision that no other fractions with such small denominators can match.

Already in ancient times, mathematicians tried to find good approximations to Pi.

The Greek mathematician Archimedes (around 250 BC) used the fraction \(\large \frac{22}{7}\), while Chinese mathematicians around the year 500 knew the much better approximation \(\large \frac{355}{113}\).

Both were used for centuries before modern mathematics and computers could give us more precise values.