A sector of a circle is a part of a circle bounded by two radii and the arc between them. The shape looks like a slice of pizza or a piece of cake.

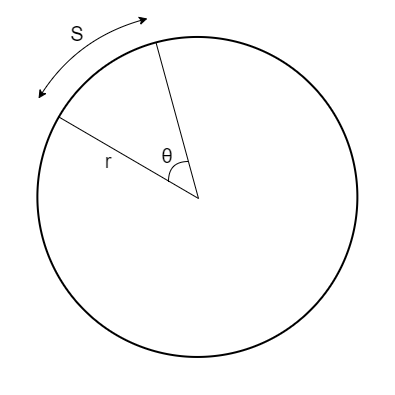
A sector of a circle is described by the radius, the angle, and the corresponding arc length. You can also calculate the area of the sector, which is always a fraction of the circle’s total area.

Angle in degrees and radians

When working with circle sectors, the angle is often measured in radians. A full circle equals \(360^\circ\) or \(2\pi\) radians.

There are simple formulas to convert between degrees and radians, and it is important to choose the right one depending on which unit of angle measurement you use.

$$ \large \theta = \frac{v_{deg} \cdot \pi}{180} $$

$$ \large v_{deg} = \frac{\theta \cdot 180}{\pi} $$

Thinking in fractions of the circle

Another way to understand a circle sector is to see the angle as a fraction of the whole circle. Since a full circle is \(360^\circ\), you can first find what one degree corresponds to and then multiply by the number of degrees in the sector.

$$ \large \frac{1}{360} \cdot \text{Circumference} = \frac{1}{360} \cdot 2 \pi r $$

$$ \large \frac{1}{360} \cdot \text{Area} = \frac{1}{360} \cdot \pi r^2 $$

In this way, you can quickly see how large a part of the circumference and area of the circle a certain number of degrees represents. For example, \(60^\circ\) gives one sixth of both circumference and area.

Example

A circle has radius \(r = 10 \,\text{cm}\), and we look at a sector with an angle of \(60^\circ\).

First, the angle is converted to radians:

$$ \large \theta = \frac{60 \cdot \pi}{180} $$

$$ \large \theta = \frac{\pi}{3} \approx 1,047 \,\text{rad} $$

The arc length is:

$$ \large S = r \cdot \theta $$

$$ \large S = 10 \cdot 1,047 $$

$$ \large S \approx 10,47 \,\text{cm} $$

The area of the sector is:

$$ \large A = \frac{1}{2} r^2 \theta $$

$$ \large A = \frac{1}{2} \cdot 100 \cdot 1,047 $$

$$ \large A \approx 52,36 \,\text{cm}^2 $$

Summary

A circle sector is therefore a part of a circle defined by the radius and an angle.

You can describe it with the angle in radians or degrees, and you can calculate both arc length and area as a fraction of the entire circle.