Tangent and cotangent

Tangent is also a trigonometric function that tells us something about the angle in the unit circle. Unlike cosine and sine, the result can be greater than 1.

The definition of tangent is:

 

$$ tan(v) = \frac{sin(v)}{cos(v)} $$

 

This means that an angle (A) of 25 degrees is calculated like this:

 

$$ tan(v) = \frac{sin(v)}{cos(v)} \qquad \Leftrightarrow $$

$$ tan(v) = \frac{sin(25^\circ)}{cos(25^\circ)} \qquad \Leftrightarrow $$

$$ tan(v) = \frac{0.423}{0.906} \qquad \Leftrightarrow $$

$$ tan(v) \approx 0.467 $$

 

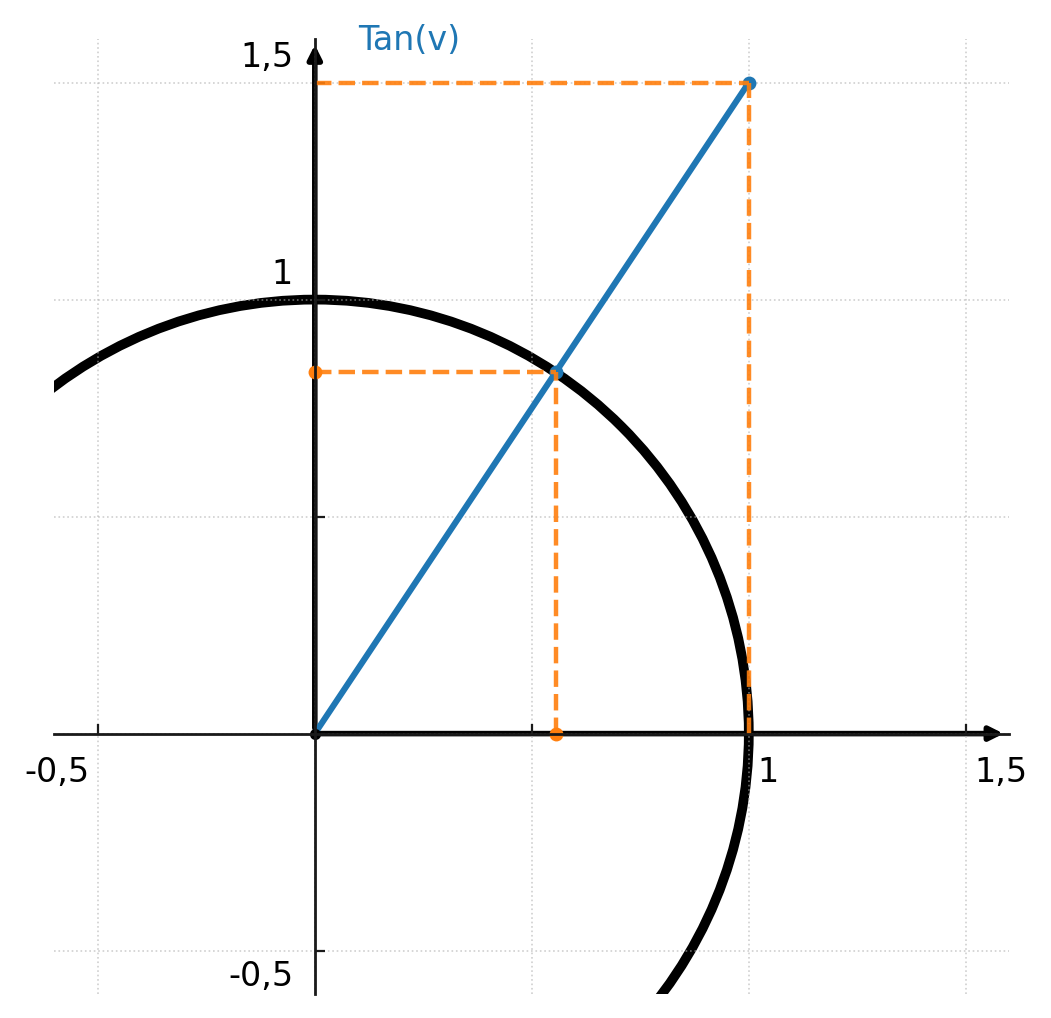
Tangent can also be read in the unit circle. You start by drawing a vertical line that is tangent to the unit circle at the point \((1, 0)\).

Then you can see where the angle intersects the line. The intersection’s y-coordinate is the tangent of the angle.

 

 

Cotangent

Cotangent is the reciprocal of tangent:

 

$$ cot(v) = \frac{cos(v)}{sin(v)} $$

 

Cotangent is not used as often, because sine, cosine, and tangent make it possible to perform the most common geometric calculations.

You will also usually not find a cot button on ordinary calculators.

 

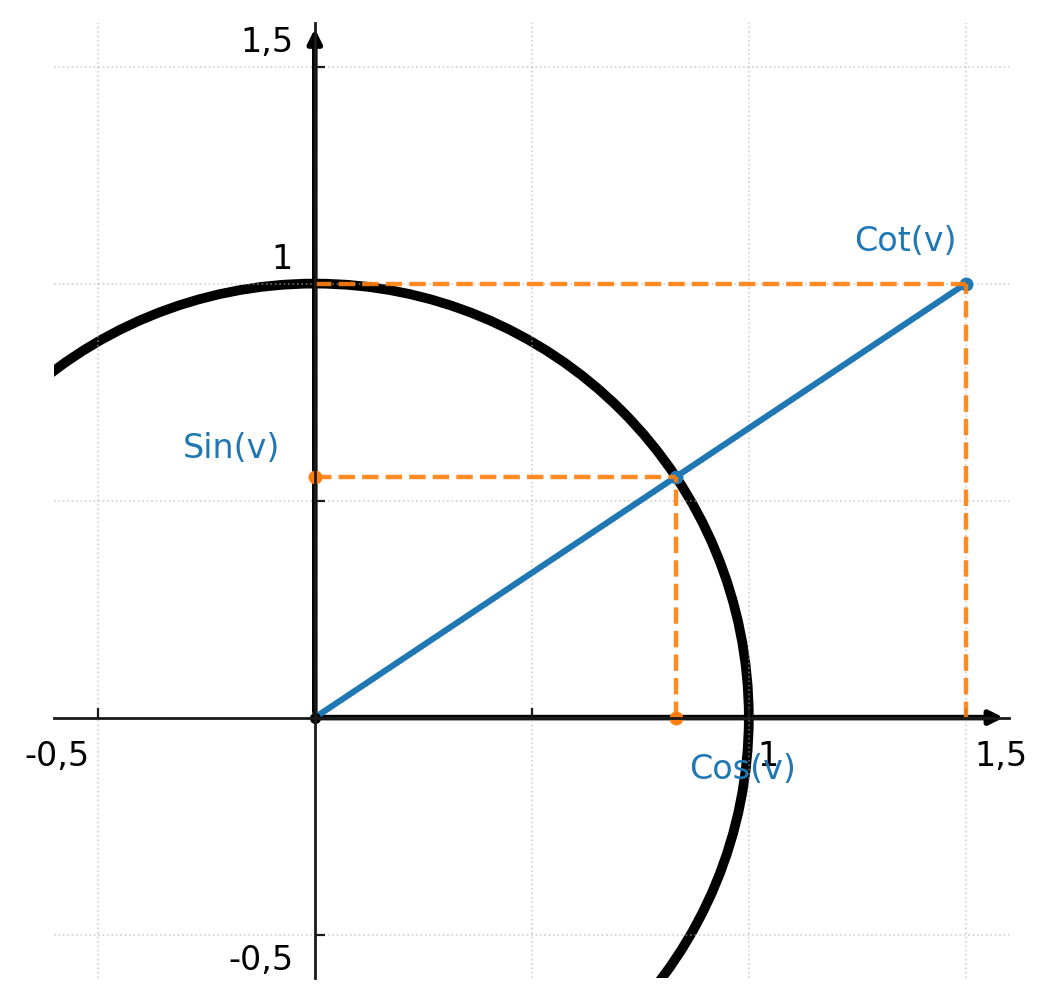
In the unit circle, cotangent runs horizontally from the point \((0,1)\) and is read on the x-axis where it intersects the angle:

 

 

The angle of 25 degrees is calculated like this:

 

$$ cot(v) = \frac{cos(v)}{sin(v)} \qquad \Leftrightarrow $$

$$ cot(v) = \frac{cos(25^\circ)}{sin(25^\circ)} \qquad \Leftrightarrow $$

$$ cot(v) = \frac{0.906}{0.423} \qquad \Leftrightarrow $$

$$ cot(v) \approx 2.14 $$

 

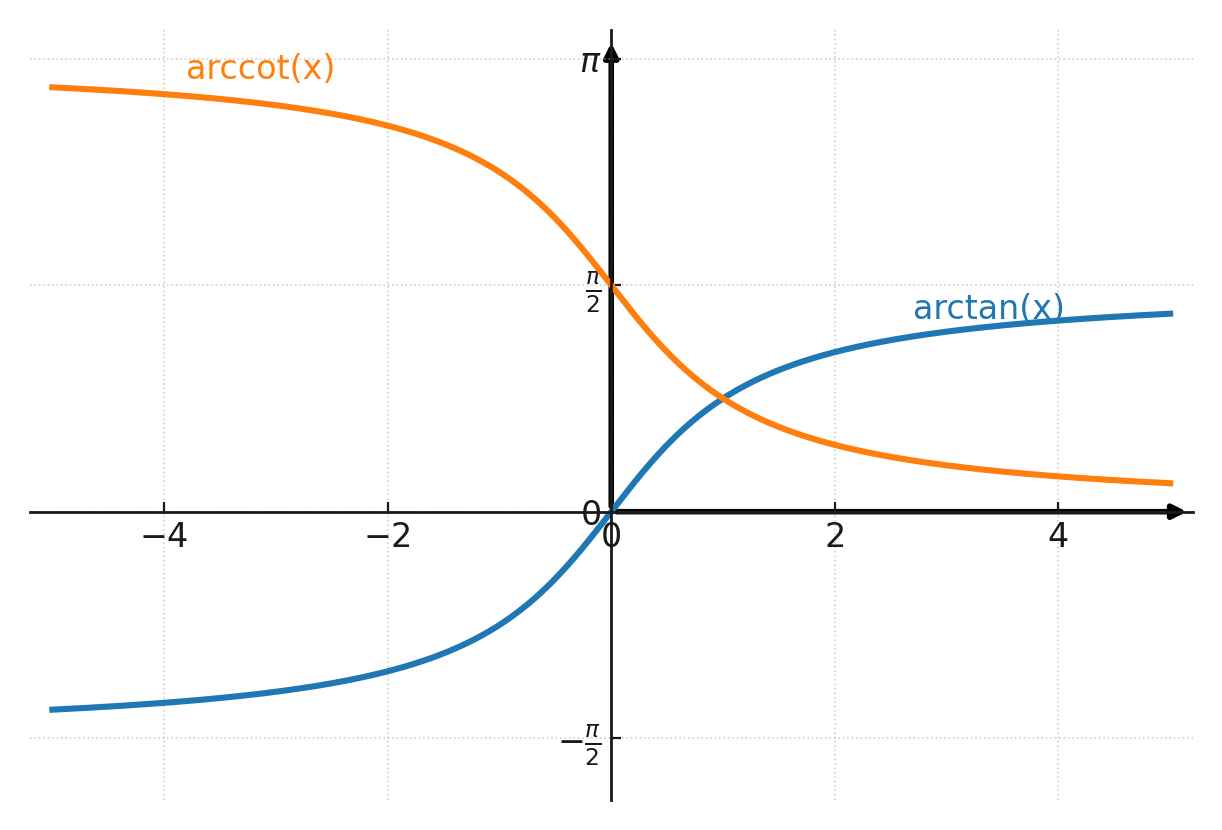
Inverse functions

Just like arcsin and arccos, there are also inverse functions for tangent and cotangent. These are called arctan and arccot (or written as tan^-1 and cot^-1).

If you know the tangent of an angle, but not the angle itself, you can find it with arctan. For example, we know that:

 

$$ tan(45^\circ) = 1 $$

 

Thus it also holds that:

 

$$ tan^{-1}(1) = 45^\circ $$

 

Arctan can be used to calculate an angle from the ratio between two sides in a right triangle.

 

Arccot works the same way for cotangent. If you know the cotangent of an angle, you can find the angle with arccot. For example:

 

$$ cot(45^\circ) = 1 \qquad \Leftrightarrow \qquad cot^{-1}(1) = 45^\circ $$

 

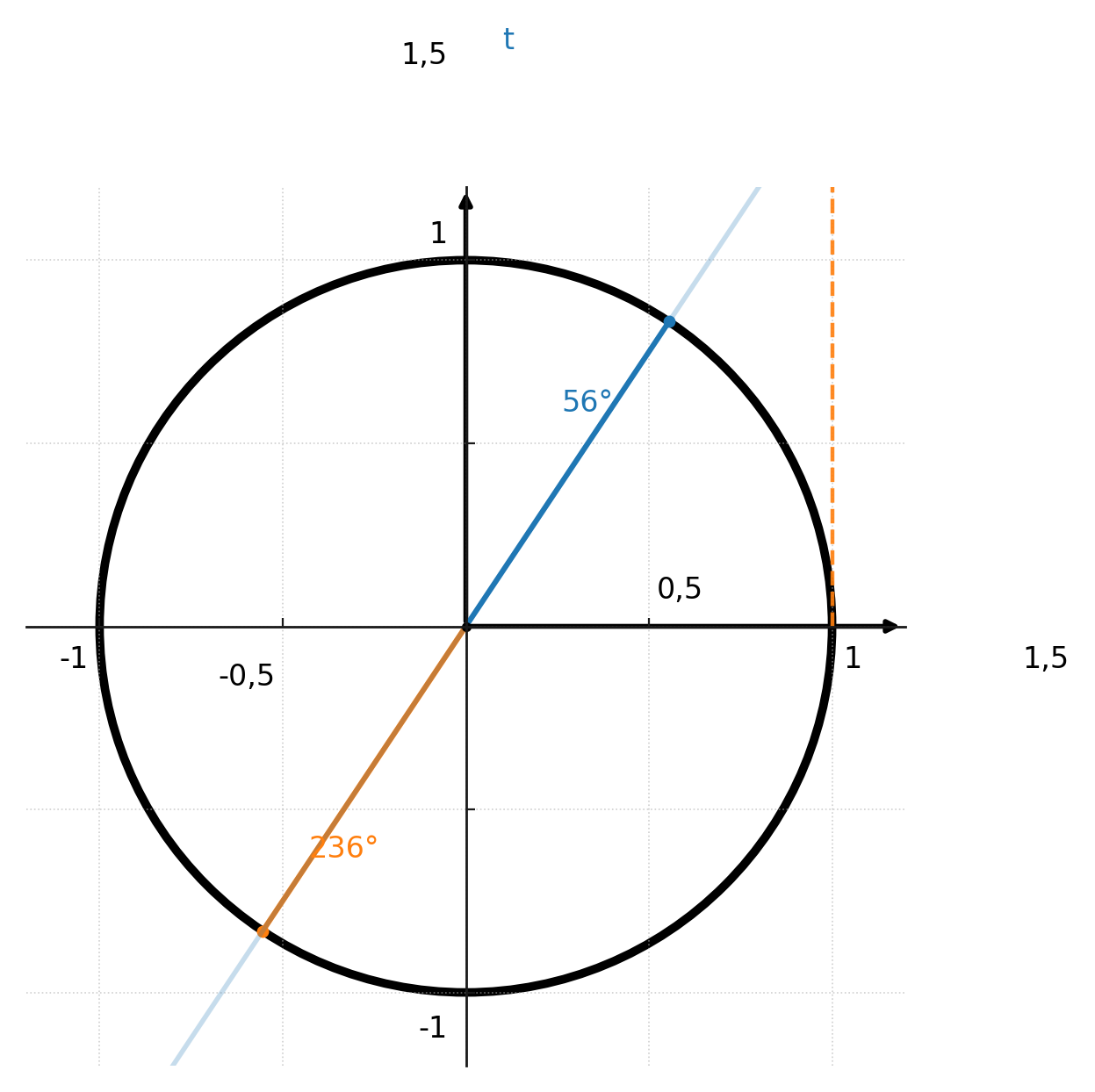
Both functions will give two solutions unless they are restricted. Here you can see arctan’s two solutions in the first and third quadrants:

 

 

The functions are restricted as follows:

 

• For arctan, the angle is restricted to the interval \(-90^\circ \leq v \leq 90^\circ\)
• For arccot, the angle is restricted to the interval \(0^\circ \leq v \leq 180^\circ\)

 

In this way, the functions are unique!

 

The two inverse functions are drawn in the coordinate system. Note that the y-axis is in radians and not degrees.