Trigonometry
Trigonometry is the study of the relationships between the sides and angles of a triangle and the calculation of the unknown quantities based on those you know.
Plane trigonometry deals with relationships in a flat triangle.
Based on the unit circle and knowledge of trigonometric functions and relations, it is possible to calculate almost all geometric figures, including spatial ones.

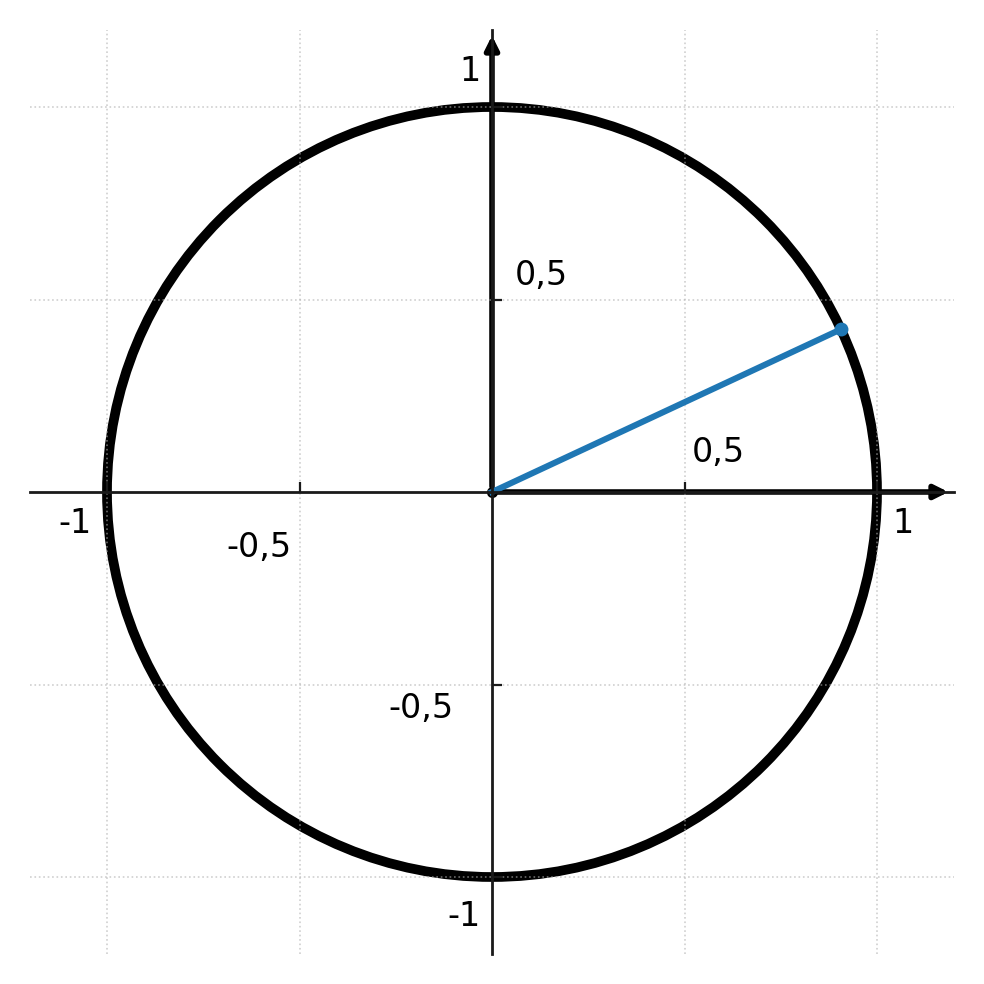
If you imagine the unit circle drawn in a coordinate system, the circle’s center is at (0,0), and it has a radius of 1.
From the unit circle, one can define three functions, cosine, sine and tangent, which are used for calculating the angles and sides of triangles.
The circumference of the unit circle is \( \large 2 \cdot \pi \).
The area of the unit circle is \( \large \pi \).
Functions and relations
There are six trigonometric functions in total. In a right triangle they are defined as follows:
| Function | Definition |
|---|---|
| Sine (sin) | \( \Large \sin(v) = \tfrac{\text{opposite side}}{\text{hypotenuse}} \) |
| Cosine (cos) | \( \Large \cos(v) = \tfrac{\text{adjacent side}}{\text{hypotenuse}} \) |
| Tangent (tan) | \( \Large \tan(v) = \tfrac{\text{opposite side}}{\text{adjacent side}} \) |
| Cotangent (cot) | \( \Large \cot(v) = \tfrac{\text{adjacent side}}{\text{opposite side}} \) |
| Secant (sec) | \( \Large \sec(v) = \tfrac{\text{hypotenuse}}{\text{adjacent side}} \) |
| Cosecant (csc) | \( \Large \csc(v) = \tfrac{\text{hypotenuse}}{\text{opposite side}} \) |
For ordinary geometry, the first three are the important ones to know. It is also important to be able to use the sine and cosine relations.
Reference line, point and angle
If you draw a line from the center (0,0) to a random point on the circle’s arc, the line will form an angle with the x-axis of the coordinate system.
The point you chose on the circle’s arc is called the reference point. The line you drew is called the reference line, and the angle formed with the x-axis is called the reference angle.
If you know the angle in a triangle, you can draw it into the circle, and the reference point will be the basis for your calculation of the triangle.
Spherical trigonometry
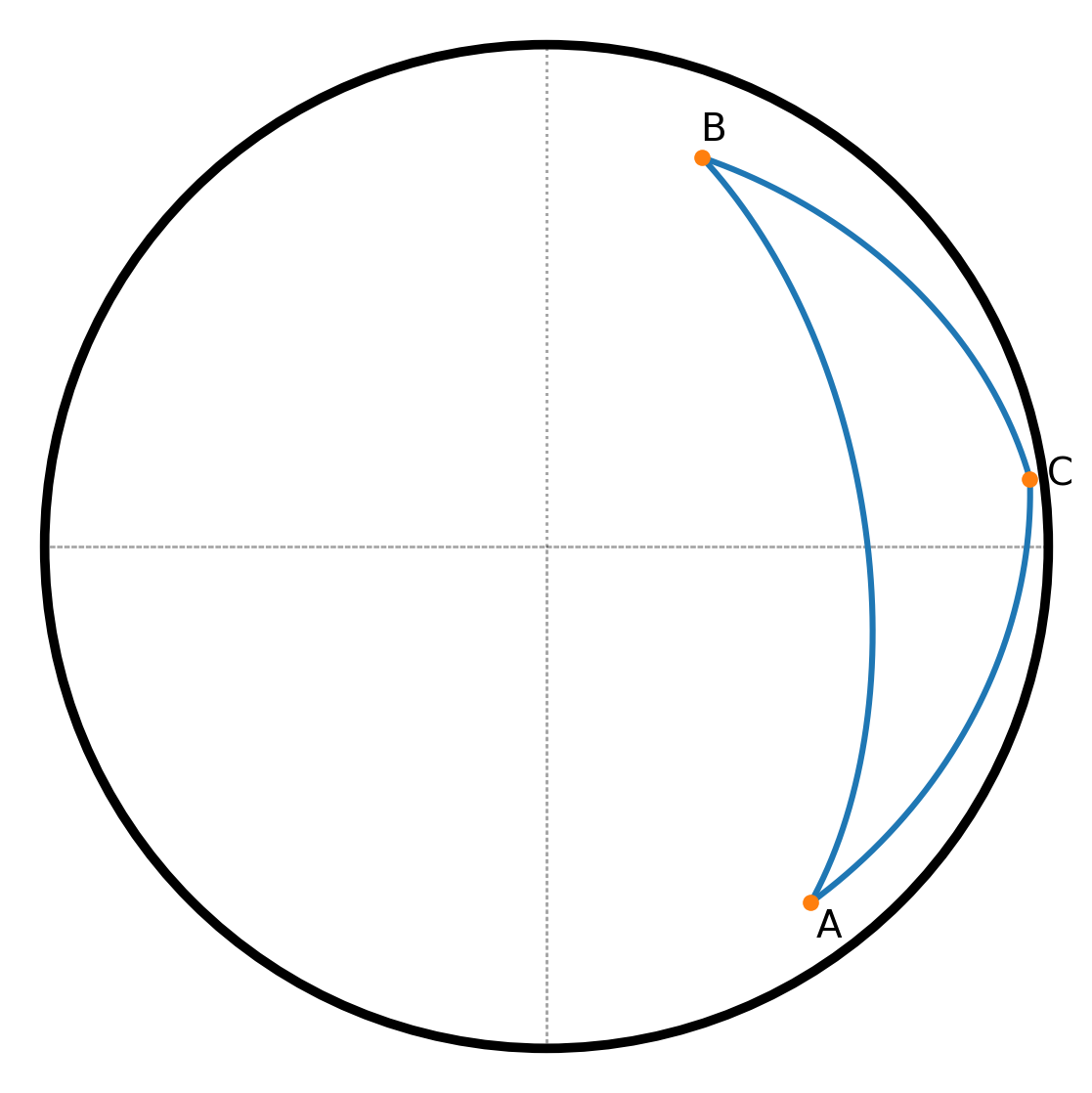
Spherical trigonometry deals with triangles and other geometric figures on the surface of a sphere.
Just as we have the unit circle with radius 1 in plane trigonometry, one can imagine a unit sphere with radius 1.
A spherical triangle is formed by three arcs from great circles on the surface of the sphere. With the help of trigonometric functions, one can calculate the interdependencies between sides and angles in such triangles.
Spherical trigonometry has especially been developed for use in navigation and astronomy.