Sine and cosine

If you draw an angle in the unit circle, you can read off cosine and sine on the circumference of the unit circle as a point in the coordinate system.

The result will always be between -1 and 1, because the point always lies on the circle with radius 1.

In the figure, an angle of 25 degrees is drawn in the unit circle, and we can read the intersection point on the x- and y-axes.

 

 

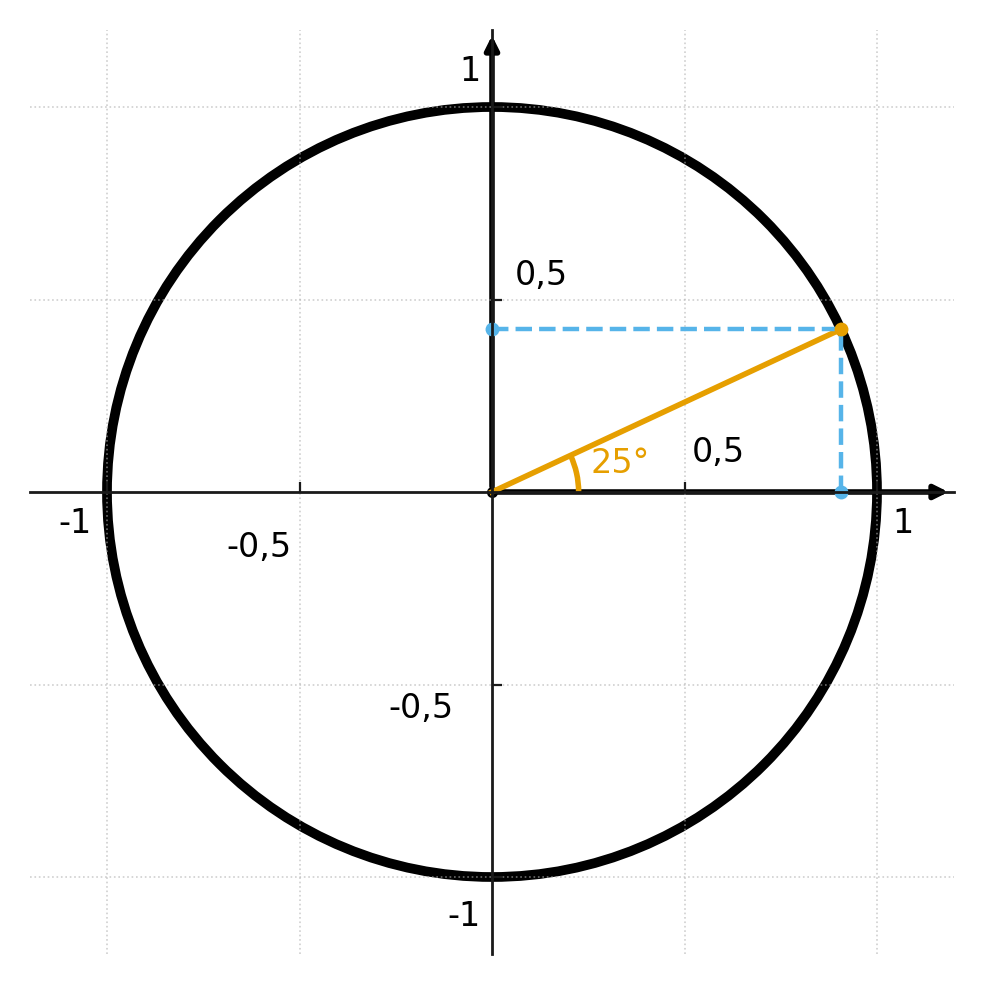
Remember that coordinates are always read as \( \large (x,y) \), which corresponds to \( \large (cosine, sine) \).

Cosine and sine are therefore the coordinate pair of the reference point – the point where the angle hits the unit circle.

The angle in the figure is 25 degrees, and if you could read it precisely enough, you would see that:

 

$$ sin(v) \approx 0.906 $$

$$ cos(v) \approx 0.423 $$

 

Of course, it is not possible to read exactly on the unit circle, and one would normally use the cosine and sine buttons on a calculator.

 

Inverse functions

If you know the cosine or sine of an angle, but not the angle itself, you can work the other way with the inverse functions. These are called arccos and arcsin (or written as cos^-1 and sin^-1).

The inverse functions are also found on a calculator, usually on the same key as the ordinary functions.

 

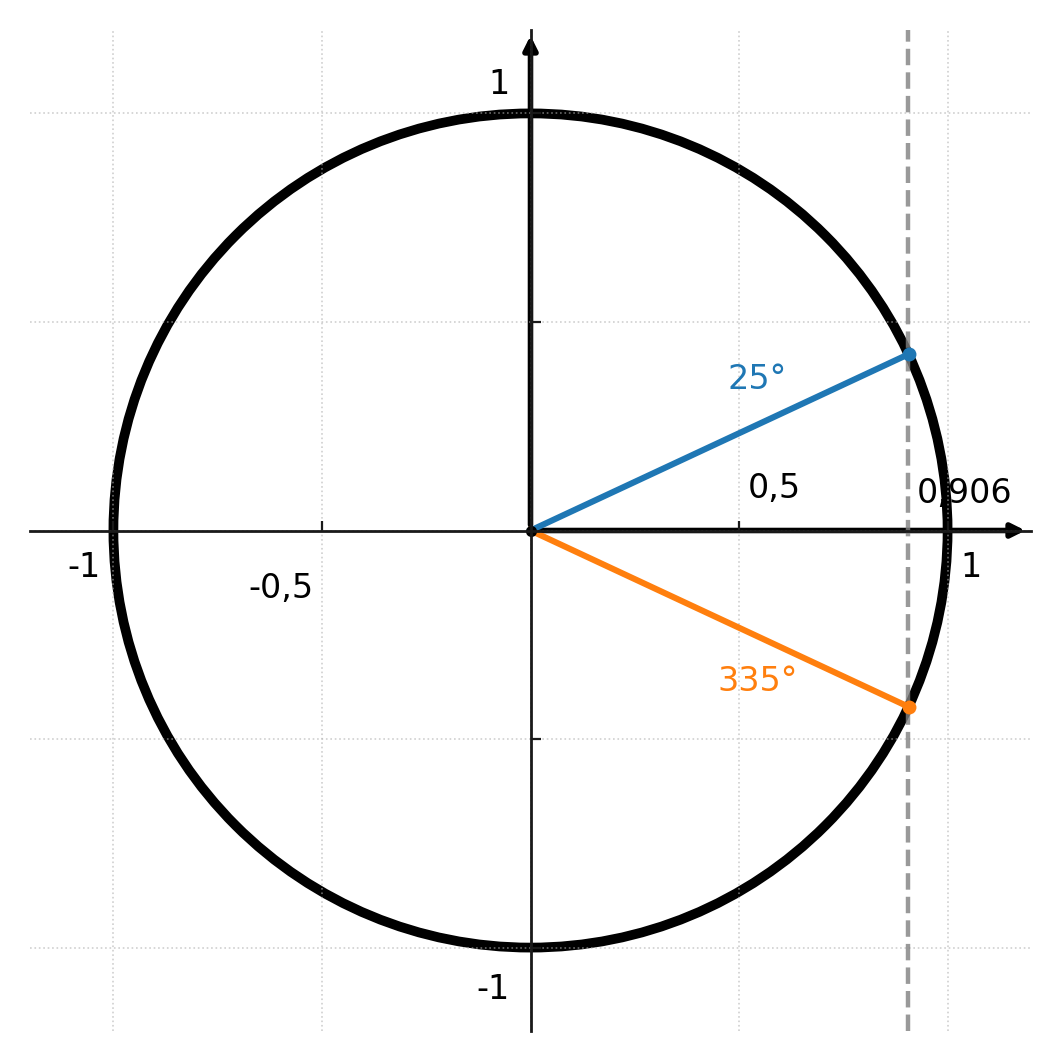
Let us assume you know that cos(A) = 0.906, but you do not know the angle. Then you can find it by:

 

$$ cos^{-1}(0.906) \approx 25^\circ $$

 

Note that the inverse functions do not always give a unique solution. For example, cos(v) = 0.906 can apply to both an angle of 25° and an angle of 335° (-25°).

To use the functions as unique inverse functions, their definition is restricted:

 

• Arccos is normally restricted to the interval \(0^\circ \leq v \leq 180^\circ\) (\(0 \leq v \leq \pi\) rad)
• Arcsin is normally restricted to the interval \(-90^\circ \leq v \leq 90^\circ\) (\(-\tfrac{\pi}{2} \leq v \leq \tfrac{\pi}{2}\) rad)

 

This means that the solution of 335° does not appear, and that arcsin always returns angles in the first or fourth quadrant.

 

 

 

 

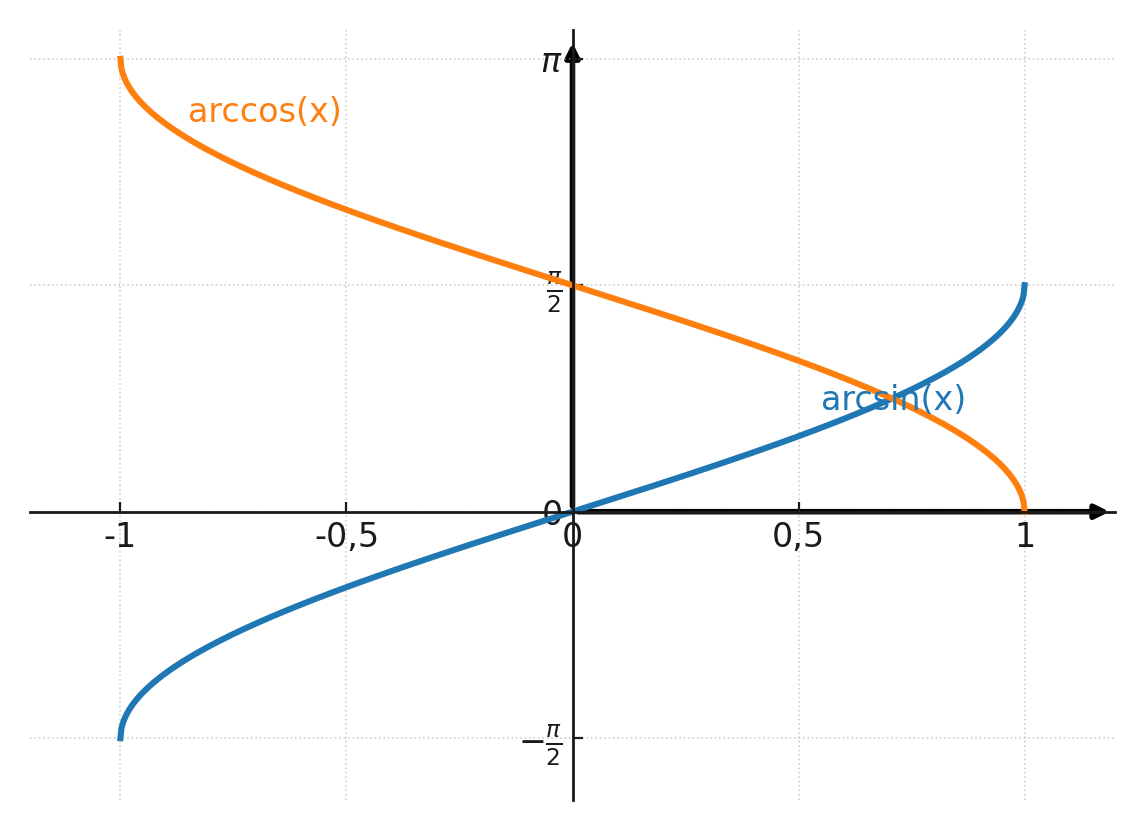
The two inverse functions are drawn in the coordinate system. Note that the y-axis is in radians and not in degrees.

If you read on the arccos curve at x = 0.906, you hit 0.44 rad which corresponds to 25°.

 

 

 

Radians and Degrees

To convert between radians and degrees, use the formula:

 

$$ \text{degrees} = \text{radians} \cdot \frac{180^\circ}{\pi} $$

$$ \text{radians} = \text{degrees} \cdot \frac{\pi}{180^\circ} $$

 

Example:

 

$$ 0.44 \,\text{rad} \approx 0.44 \cdot \tfrac{180^\circ}{\pi} \approx 25^\circ $$