Law of cosines

The law of cosines can be used in arbitrary triangles – that is, triangles that are neither right-angled, isosceles, nor equilateral. It works both when you know two sides and the included angle and when you know all three sides.

 

Formulas of the law of cosines

If you know an angle and the two sides that form the angle, you can find the third side using the law of cosines:

 

$$ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(A) $$

$$ b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(B) $$

$$ c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(C) $$

 

Note: if the triangle is right-angled, you can simply use the Pythagorean theorem. The law of cosines is particularly useful for arbitrary triangles.

 

Calculation of angles

If you know all three sides of a triangle, you can find the angles by isolating cosine in the formula:

 

$$ \cos(A) = \frac{b^2 + c^2 - a^2}{2 \cdot b \cdot c} $$

$$ \cos(B) = \frac{a^2 + c^2 - b^2}{2 \cdot a \cdot c} $$

$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2 \cdot a \cdot b} $$

 

The result will be a number between -1 and 1. To find the angle, you use \( \cos^{-1} \) on your calculator:

 

$$ \cos^{-1}(0,866) = 30^\circ $$

 

The angle is therefore 30 degrees.

 

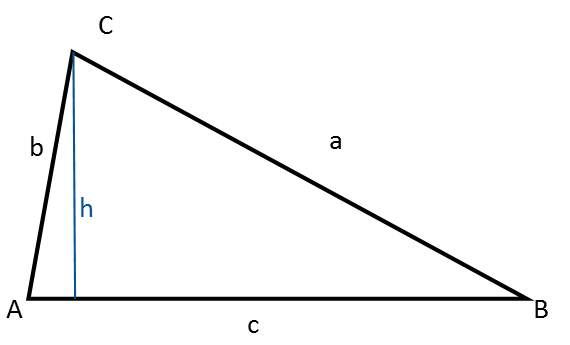
An arbitrary triangle is neither right-angled, equilateral, nor isosceles.

Note that the height divides it into two right-angled triangles.