Statistisk sandsynlighed

Sandsynlighed kan beregnes på to måder: teoretisk (klassisk) og statistisk (empirisk).

 

Klassisk sandsynlighed

Hvis man kender udfaldsrummet og alle udfald er lige sandsynlige, kan man bruge formlen:

 

$$ \large P(A) = \frac{\text{antal gunstige udfald}}{\text{antal mulige udfald}} $$

 

Eksempel: Sandsynligheden for at slå en sekser med en terning er:

 

$$ \large \frac{1}{6} \approx 0,167 = 16,7\% $$

 

 

Statistisk (empirisk) sandsynlighed

Nogle gange kan man ikke regne sandsynligheden direkte ud. I stedet udfører man forsøg eller eksperimenter og bruger observationerne til at beregne sandsynligheden.

 

Eksempel: Vi kaster en terning 1.000 gange og noterer hyppighed og frekvens:

 

	1	2	3	4	5	6
$$ h(x) $$	$$ 180 $$	$$ 176 $$	$$ 149 $$	$$ 170 $$	$$ 167 $$	$$ 158 $$
$$ f(x) $$	$$ \tfrac{180}{1000} $$	$$ \tfrac{176}{1000} $$	$$ \tfrac{149}{1000} $$	$$ \tfrac{170}{1000} $$	$$ \tfrac{167}{1000} $$	$$ \tfrac{158}{1000} $$
Forventet	$$ \tfrac{1000}{6} \approx 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$

 

 

Diagram

Søjlediagrammet herunder viser den teoretiske sandsynlighed (167 for hver side) sammenlignet med de empiriske udfald.

 

 

 

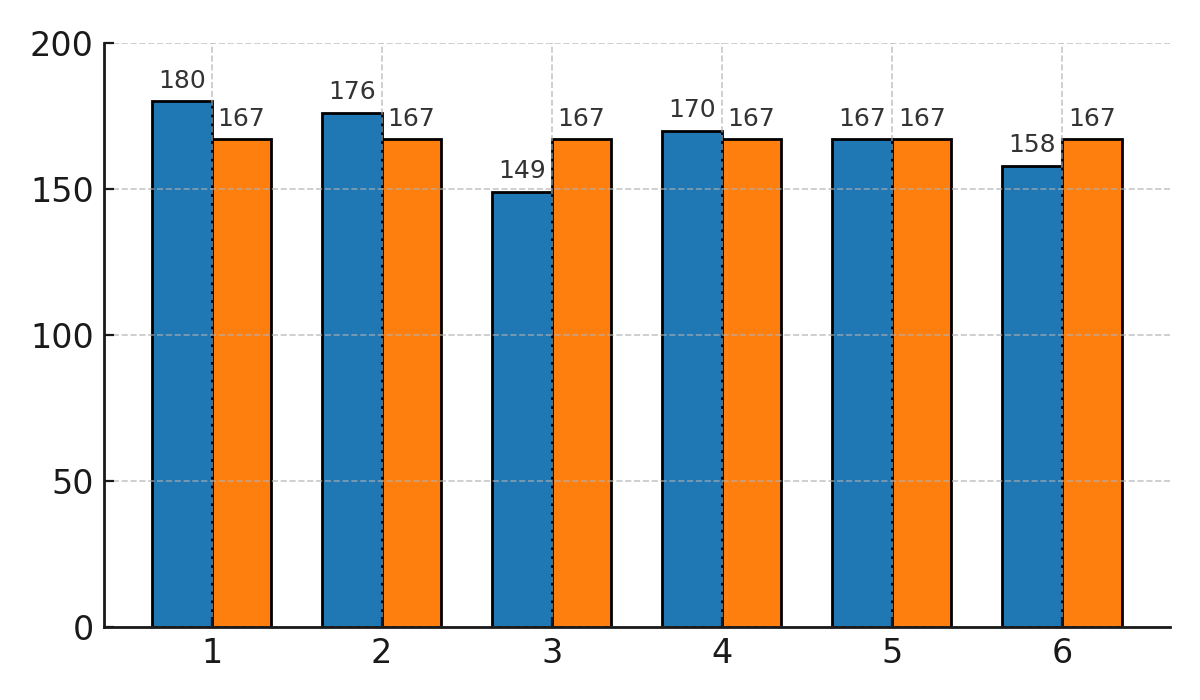
Sammenligning

Vi ved at sandsynligheden for at slå en sekser er:

 

$$ \large \tfrac{1}{6} \approx 0,167 = 16,7\% $$

 

Vores eksperiment viste i stedet:

 

$$ \large \tfrac{158}{1000} = 0,158 = 15,8\% $$

 

Resultatet er ikke præcis det samme som den teoretiske værdi, men det ligger tæt på. Det viser hvordan statistisk sandsynlighed bruges til at nærme sig den teoretiske sandsynlighed gennem observationer.

 

Statistisk sandsynlighed er derfor et praktisk værktøj, når man ikke kan beregne sandsynligheden direkte, men i stedet må basere sig på observationer.