Sinusrelationen
Sinusrelationen kan bruges i de tilfælde, hvor man kender et vinkel-side-par, altså hvor den ene af de kendte sider ligger overfor den kendte vinkel.
Dvs. at hvis du kender vinkel \(A\) og siderne \(a\) og \(b\), så skal du bruge sinusrelationen.
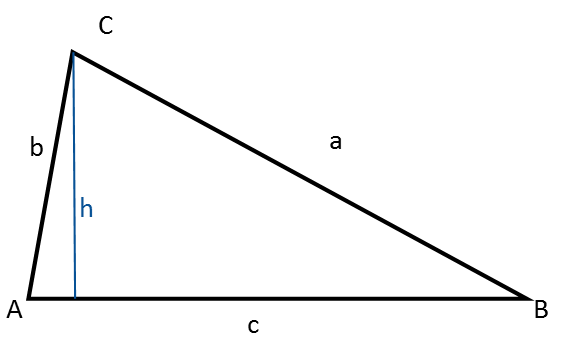
En vilkårlig trekant er hverken retvinklet, ligesidet eller ligebenet.
Sinusrelationen ser sådan ud:
$$ {a \over \sin(A)} = {b \over \sin(B)} = {c \over \sin(C)} $$
Så hvis du kender vinkel \(A\) og siderne \(a\) og \(b\), og skal finde vinkel \(B\), bruger du følgende og isolerer vinkel \(B\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] \sin(B) = {b \cdot \sin(A) \over a} $$
Resultatet vil blive et tal mellem 0 og 1, f.eks. 0,866. For at finde vinklen skal du bruge \( \sin^{-1} \) på din lommeregner:
$$ \sin^{-1}(0,866) = 60^\circ $$
Vinklen er altså 60 grader.
Kender du to vinkler og kun én side, kan du også bruge sinusrelationen. Lad os antage at du kender vinkel \(A\) og \(B\), samt siden \(a\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] b = {a \cdot \sin(B) \over \sin(A)} $$
Bemærk: Hvis beregningen giver \(\sin(v) > 1\), findes der ingen løsning. Det betyder, at den givne trekant ikke kan eksistere med de oplysninger, du har.
Sinus og stumpvinklede trekanter
Hvis du beregner vinkler med sinus i en trekant, der viser sig at være stumpvinklet, skal du passe på – der kan optræde to resultater afhængigt af, hvor meget du ved om trekanten.
Lad os antage at du har følgende oplysninger om en trekant:
- Vinkel A = 25 grader
- Side a = 3
- Side c = 5
Med disse oplysninger kan vi beregne vinkel \(C\):
$$ \begin{align}{a \over \sin(A)} &= {c \over \sin(C)} \Leftrightarrow \\[10pt] \sin(C) &= {c \cdot \sin(A) \over a } \Leftrightarrow \\[10pt] \sin(C) &= {5 \cdot \sin(25^\circ) \over 3 } \Leftrightarrow \\[10pt] \sin(C) &= 0,704 \Leftrightarrow \\[10pt] \sin^{-1}(0,704) &= 44,78^\circ \end{align} $$
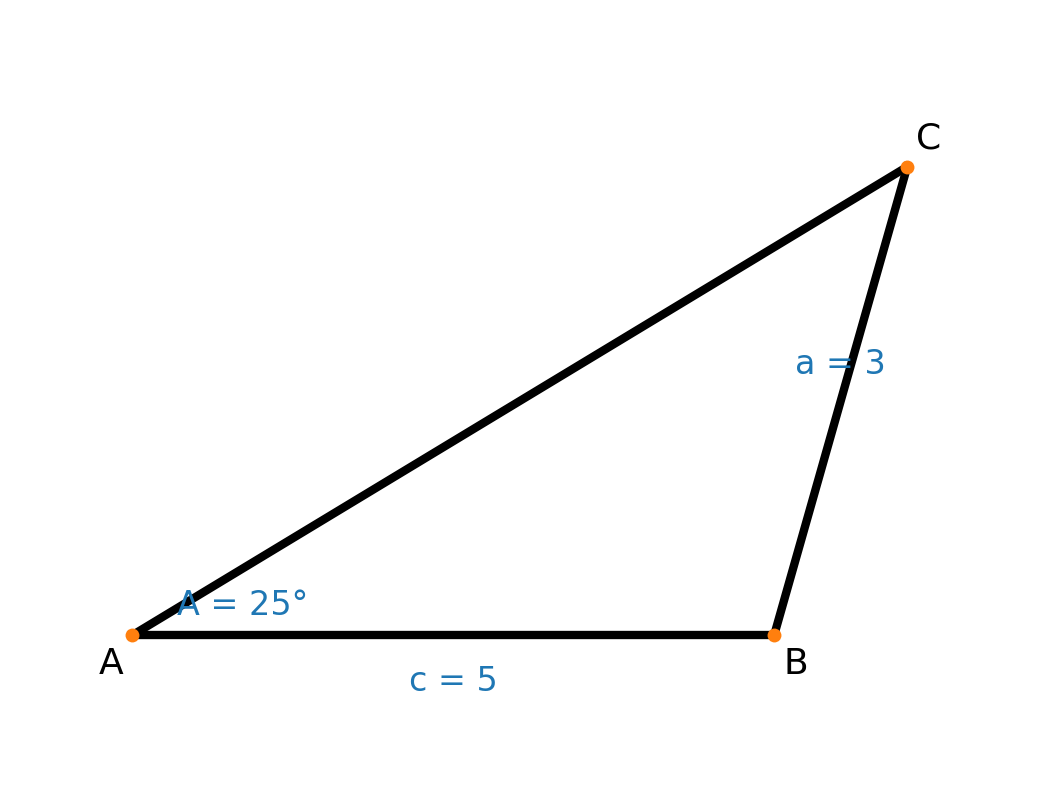
Resultatet bliver altså en trekant, som vist herover, med:
- Vinkel A = 25°
- Vinkel B = 110,22°
- Vinkel C = 44,78°.
Beregning af den stumpe vinkel
Ser du på figuren herunder, kan du se, at det er muligt at tegne en anden trekant med de samme oplysninger.
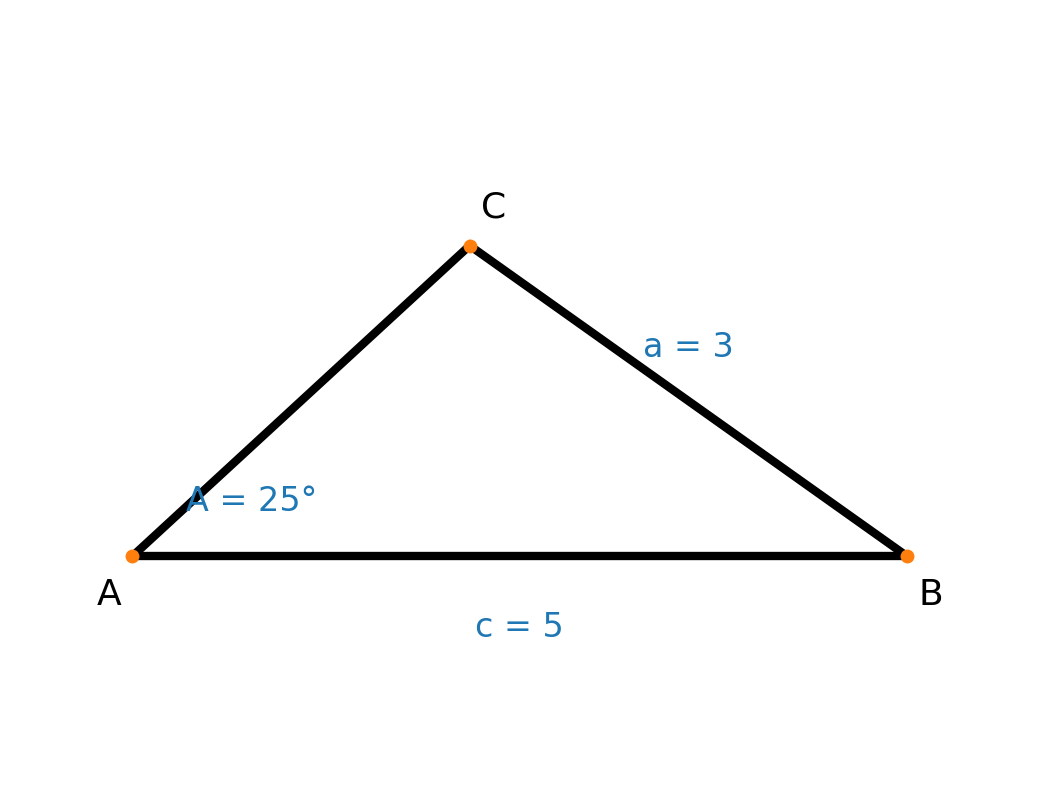
Sinusrelationen returnerer altid den spidse løsning (mellem 0° og 90°). Den mulige stumpvinklede løsning findes ved at trække den fundne vinkel fra 180°.
Vi antager, at den spidse vinkel er 44,78°, som beregnet tidligere, og kalder den \(C_1\). Den stumpe vinkel kalder vi \(C_2\):
$$ C_2 = 180 - C_1 \Leftrightarrow \\[12pt] C_2 = 135,22^\circ $$
Nu kender du vinkel \(C\) for begge trekanter og kan regne resten ud for dem begge.
Det betyder nemlig, at side \(b\) også har to forskellige længder. (Samme gælder for omkreds, højde og areal.)
Derfor skal man altid kontrollere, om den fundne løsning kan have en stump vinkel, når man bruger sinusrelationen.
Reglen for hvornår der er to løsninger er: Hvis den vinkel du regner ud med sinusrelationen bliver mindre end 90 grader, vil der være to resultater.