Addition og subtraktion af vinkler

I trigonometri beskriver addition og subtraktion af vinkler de formler, der viser hvordan sinus, cosinus og tangens ændrer sig, når man lægger to vinkler sammen eller trækker dem fra hinanden.

Formlerne gør det muligt at beregne værdier for nye vinkler ud fra kendte.

For eksempel kan man regne cos(75°), selvom den ikke står i tabellerne, ved at bruge cos(45° + 30°).

Formler for addition og subtraktion

Cosinus:

$$ \large \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) $$

$$ \large \cos(\alpha - \beta) = \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta) $$

Sinus:

$$ \large \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) $$

$$ \large \sin(\alpha - \beta) = \sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) $$

Tangens:

$$ \large \tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \cdot \tan(\beta)} $$

$$ \large \tan(\alpha - \beta) = \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)} $$

Eksempel

Vi ønsker at beregne $ \cos(75^\circ) $. Det kan skrives som $ \cos(45^\circ + 30^\circ) $:

$$ \large \cos(75^\circ) = \cos(45^\circ + 30^\circ) $$

$$ \large = \cos(45^\circ) \cdot \cos(30^\circ) - \sin(45^\circ) \cdot \sin(30^\circ) $$

$$ \large = \tfrac{\sqrt{2}}{2} \cdot \tfrac{\sqrt{3}}{2} - \tfrac{\sqrt{2}}{2} \cdot \tfrac{1}{2} $$

$$ \large = \tfrac{\sqrt{6}}{4} - \tfrac{\sqrt{2}}{4} = \tfrac{\sqrt{6} - \sqrt{2}}{4} $$

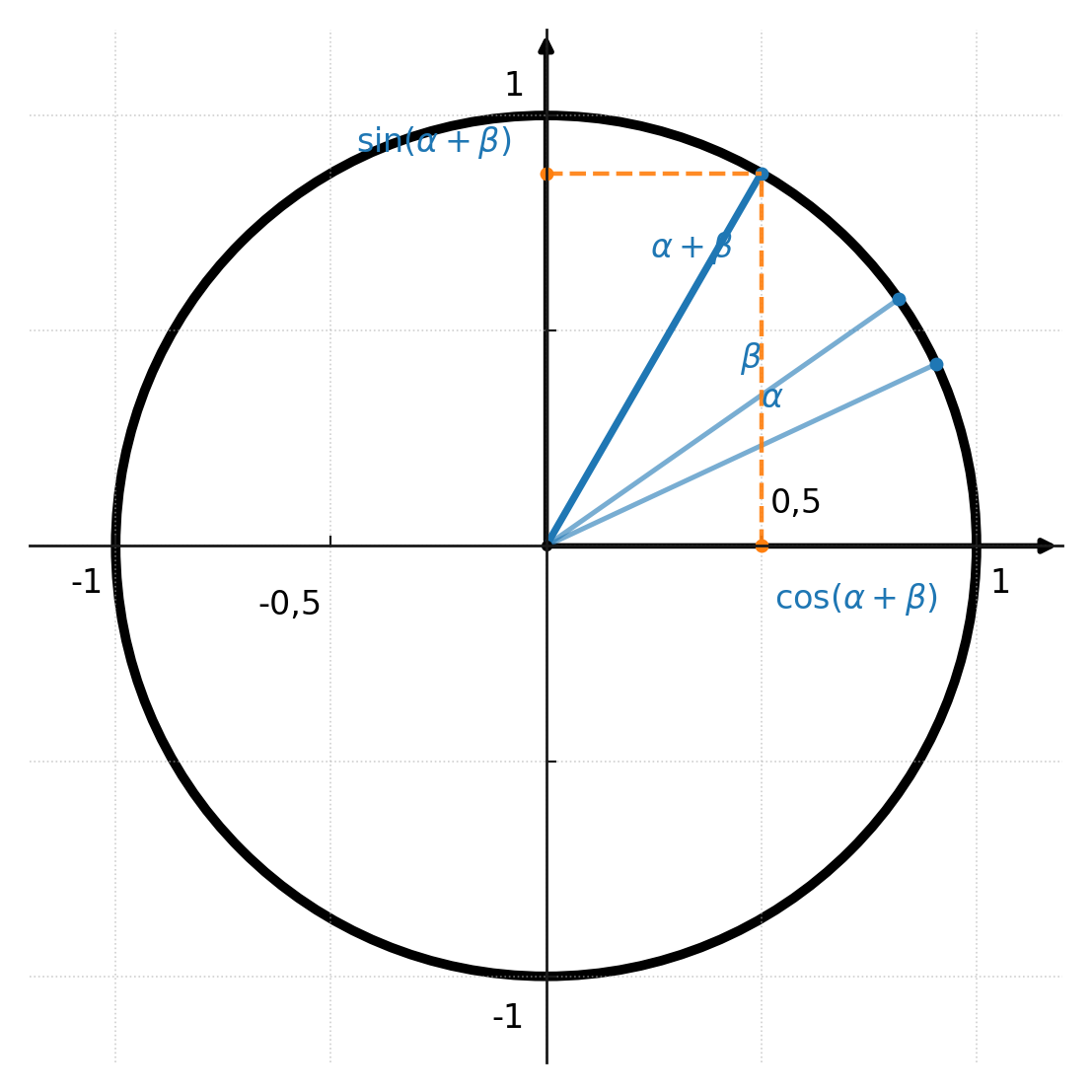
Formlerne kan også forstås geometrisk ud fra enhedscirklen.

Anvendelse

Man kan udregne præcise værdier for vinkler som 15°, 75° og 105°.
Formlerne er grundlag for dobbeltvinkel- og halvvinkelformler (ved at sætte $ \alpha = \beta $).
De bruges i beviser og identiteter i avanceret trigonometri og analyse.