Cosinusrelationen
Cosinusrelationen kan bruges i vilkårlige trekanter – altså trekanter der hverken er retvinklede, ligebenede eller ligesidede. Den fungerer både når du kender to sider og den mellemliggende vinkel og når du kender alle tre sider.
Cosinusrelationens formler
Hvis du kender en vinkel og de to sider der danner vinklen, kan du finde den tredje side ved hjælp af cosinusrelationen:
$$ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(A) $$
$$ b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(B) $$
$$ c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(C) $$
Bemærk: hvis trekanten er retvinklet, kan du nøjes med Pythagoras’ læresætning. Cosinusrelationen er særligt nyttig til vilkårlige trekanter.
Beregning af vinkler
Kender du alle tre sider i en trekant, kan du finde vinklerne ved at isolere cosinus i formlen:
$$ \cos(A) = \frac{b^2 + c^2 - a^2}{2 \cdot b \cdot c} $$
$$ \cos(B) = \frac{a^2 + c^2 - b^2}{2 \cdot a \cdot c} $$
$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2 \cdot a \cdot b} $$
Resultatet bliver et tal mellem -1 og 1. For at finde vinklen bruger du \( \cos^{-1} \) på din lommeregner:
$$ \cos^{-1}(0,866) = 30^\circ $$
Vinklen er altså 30 grader.
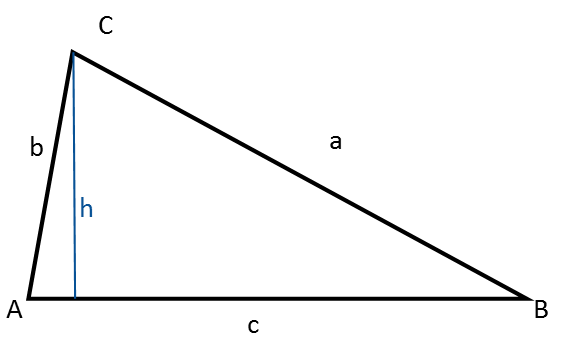
En vilkårlig trekant er hverken retvinklet, ligesidet eller ligebenet.
Bemærk at højden opdeler den i to retvinklede trekanter.