Trinonometri
Trigonometri er læren om sammenhænge mellem siderne og vinklerne i en trekant og om beregning af de ubekendte størrelser ud fra dem, du kender.
Den plane trigonometri omhandler forhold i en plan trekant.
Med udgangspunkt i enhedscirklen og viden om trigonometriske funktioner og relationer er det muligt at beregne stort set alle geometriske figurer, også rumgeometriske.

Hvis du forestiller dig enhedscirklen tegnet i et koordinatsystem, er cirklens centrum i (0,0), og den har en radius på 1.
Ud fra enhedscirklen kan man definere tre funktioner, cosinus, sinus og tangens, som anvendes til beregning af trekanters vinkler og sider.
Enhedscirklens omkreds er \( \large 2 \cdot \pi \).
Enhedscirklens areal er \( \large \pi \).
Funktioner og relationer
Der findes i alt seks trigonometriske funktioner. I en retvinklet trekant defineres de sådan her:
| Funktion | Definition |
|---|---|
| Sinus (sin) | \( \Large \sin(v) = \tfrac{\text{modstående katete}}{\text{hypotenuse}} \) |
| Cosinus (cos) | \( \Large \cos(v) = \tfrac{\text{hosliggende katete}}{\text{hypotenuse}} \) |
| Tangens (tan) | \( \Large \tan(v) = \tfrac{\text{modstående katete}}{\text{hosliggende katete}} \) |
| Cotangens (cot) | \( \Large \cot(v) = \tfrac{\text{hosliggende katete}}{\text{modstående katete}} \) |
| Secans (sec) | \( \Large \sec(v) = \tfrac{\text{hypotenuse}}{\text{hosliggende katete}} \) |
| Cosecans (csc) | \( \Large \csc(v) = \tfrac{\text{hypotenuse}}{\text{modstående katete}} \) |
Til almindelig geometri er det de tre første, der er vigtige at kunne anvende. Det er også vigtigt at kunne anvende sinus- og cosinusrelationerne.
Retningslinje, punkt og vinkel
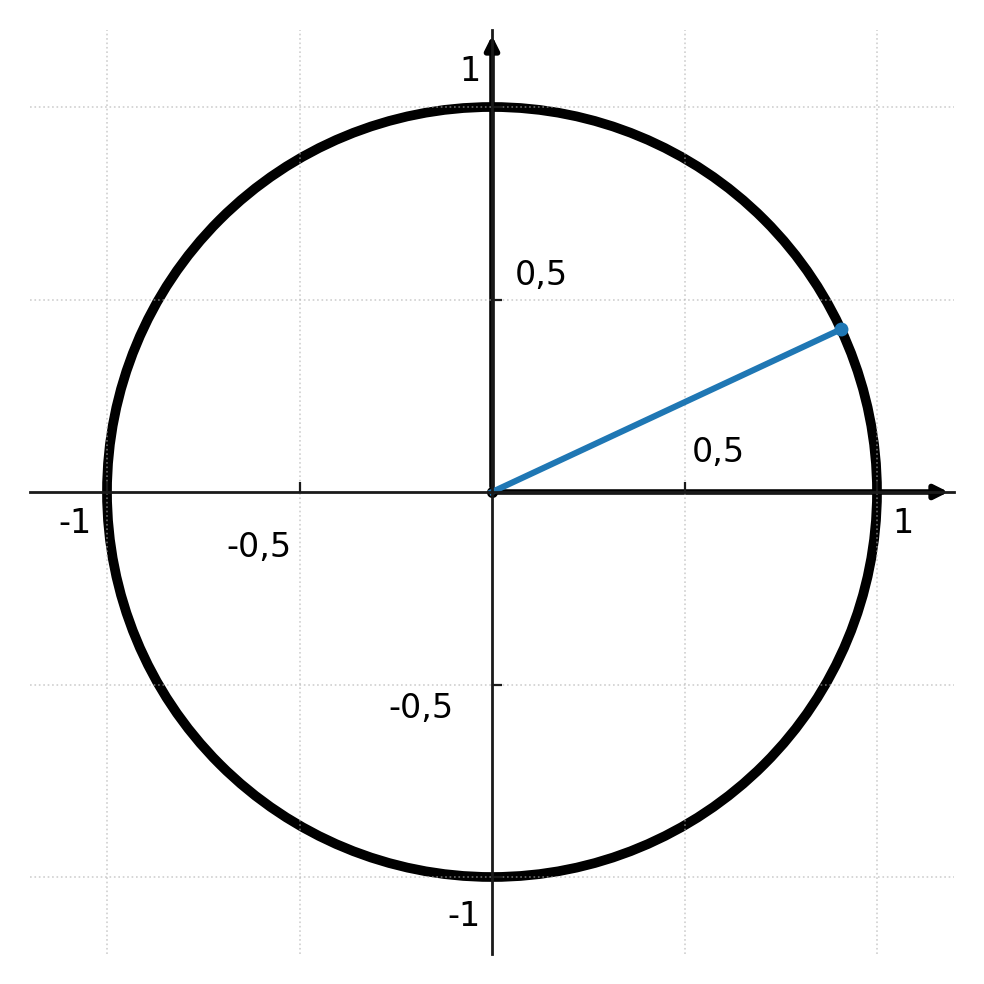
Hvis du tegner en linje fra centrum (0,0) til et tilfældigt punkt på cirklens bue, vil linjen danne en vinkel med koordinatsystemets x-akse.
Punktet, du valgte på cirkelbuen, kaldes retningspunktet. Linjen, du tegnede, kaldes retningslinjen, og vinklen, der dannes med x-aksen, kaldes retningsvinklen.
Hvis du kender vinklen i en trekant, kan du tegne den ind i cirklen, og retningspunktet vil være udgangspunkt for din beregning af trekanten.
Sfærisk trigonometri
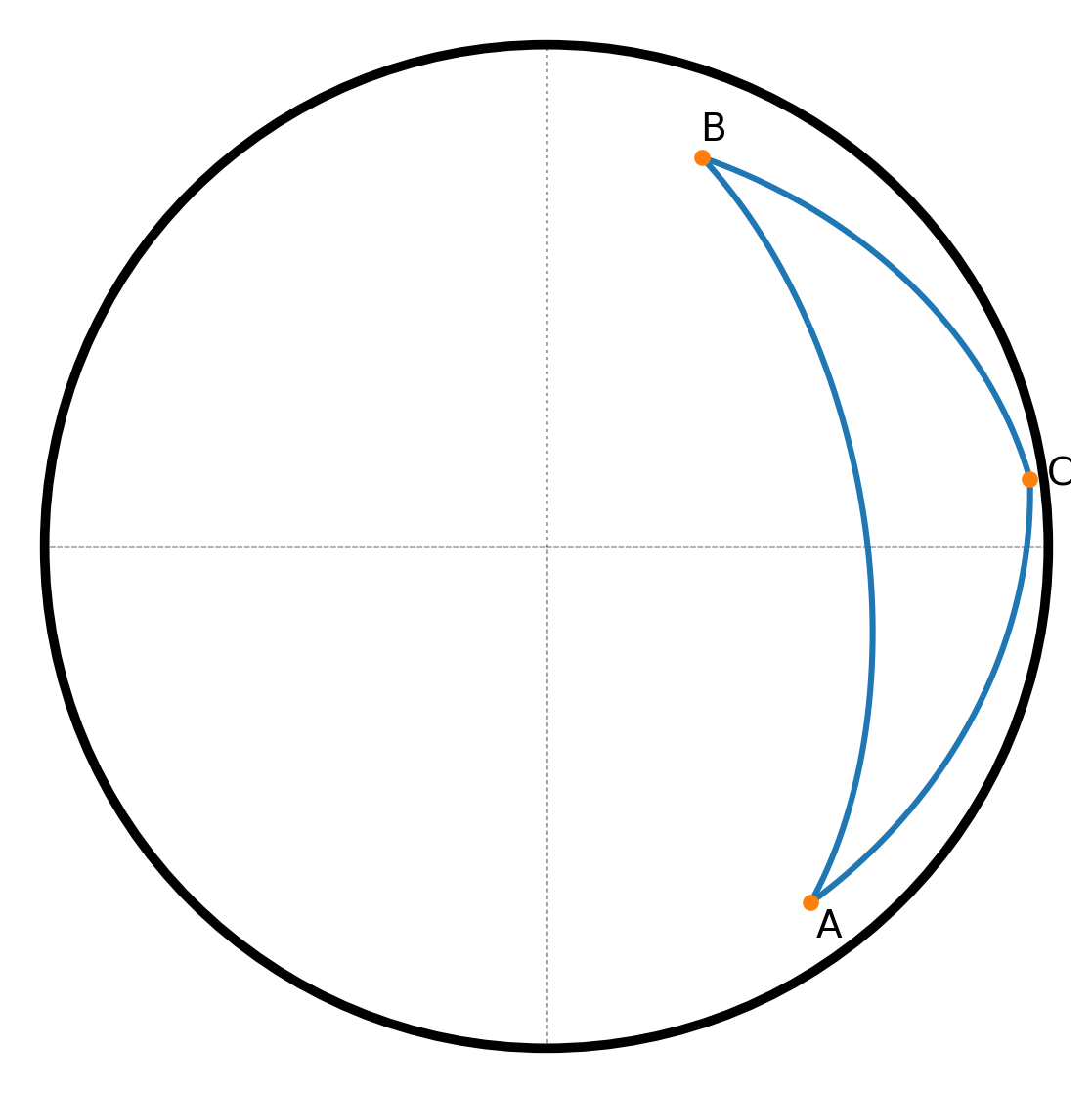
Sfærisk trigonometri beskæftiger sig med trekanter og andre geometriske figurer på overfladen af en kugle.
Ligesom vi har enhedscirklen med radius 1 til plan trigonometri, kan man forestille sig en enhedskugle med radius 1.
En sfærisk trekant dannes af tre buer fra storcirkler på kuglens overflade. Ved hjælp af trigonometriske funktioner kan man beregne de indbyrdes afhængigheder mellem sider og vinkler i sådanne trekanter.
Sfærisk trigonometri er især blevet udviklet til brug i navigation og astronomi.