Tangens og cotangens

Tangens er også en trigonomisk funktion, der fortæller noget om vinklen i enhedscirklen. I modsætning til cosinus og sinus, kan resultatet godt blive større end 1.

Definitionen af tangens er:

 

$$ tan(v) = \frac{sin(v)}{cos(v)} $$

 

Det betyder, at en vinkel (A), på 25 grader, regnes sådan her:

 

$$ tan(v) = \frac{sin(v)}{cos(v)} \qquad \Leftrightarrow $$

$$ tan(v) = \frac{sin(25^\circ)}{cos(25^\circ)} \qquad \Leftrightarrow $$

$$ tan(v) = \frac{0.423}{0.906} \qquad \Leftrightarrow $$

$$ tan(v) \approx 0.467 $$

 

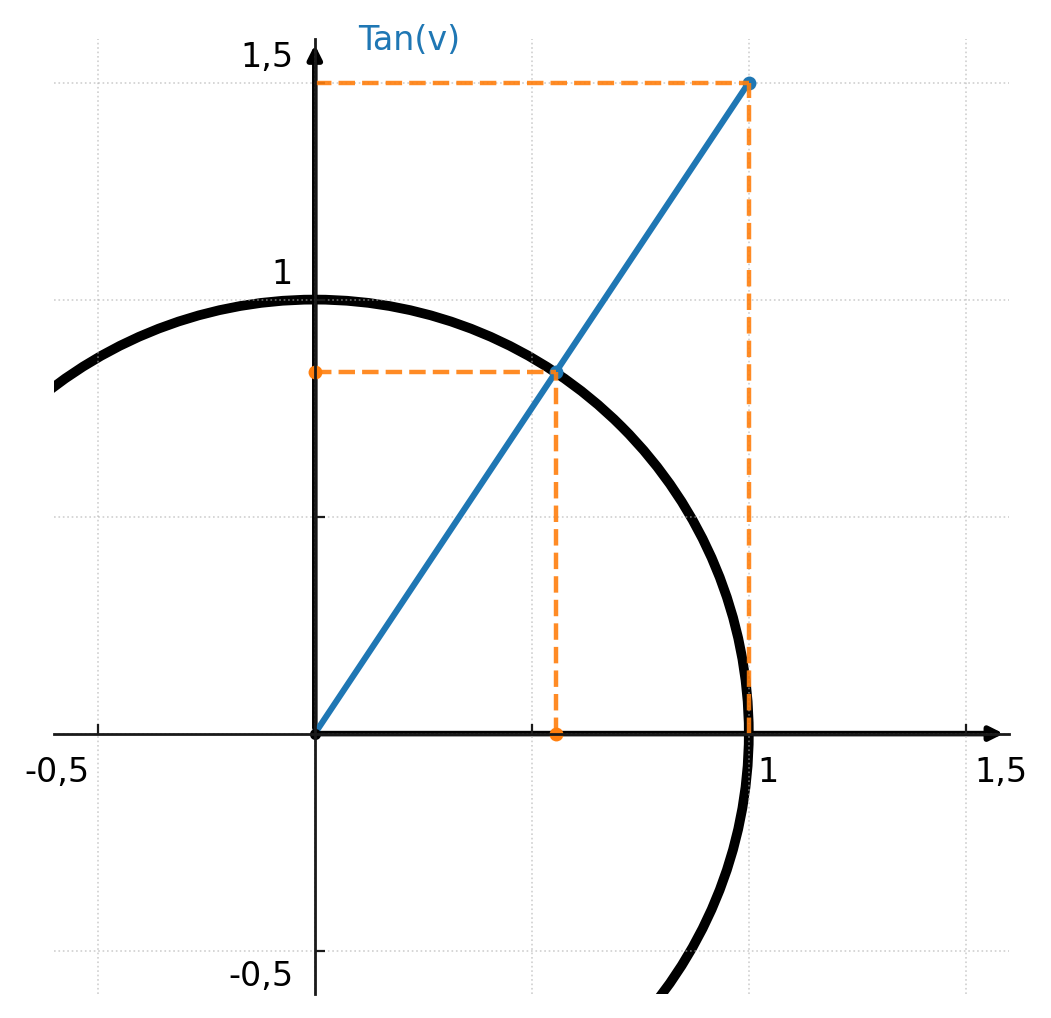
Tangens kan også aflæses i enhedscirklen. Man starter med at tegne en lodret linie, der tangerer enhedscirklen i punktet \((1, 0) \).

Så kan man se hvor vinklen skærer linien. Skæringspunktets y-koordinat er tangens til vinklen.

 

 

Cotangens

Cotangens er det omvendte af tangens:

 

$$ cot(v) = \frac{cos(v)}{sin(v)} $$

 

Cotangens anvendes ikke så ofte, fordi sinus, cosinus og tangens gør det muligt at foretage de mest almindelige geometriske regnestykker.

Du vil som regel heller ikke finde en cot knap på almindelige lommeregnere. 

 

I enhedscirklen går cotangens vandret ud fra punktet \((0,1)\) og aflæses på x-aksen, hvor den skærer vinklen:

 

 

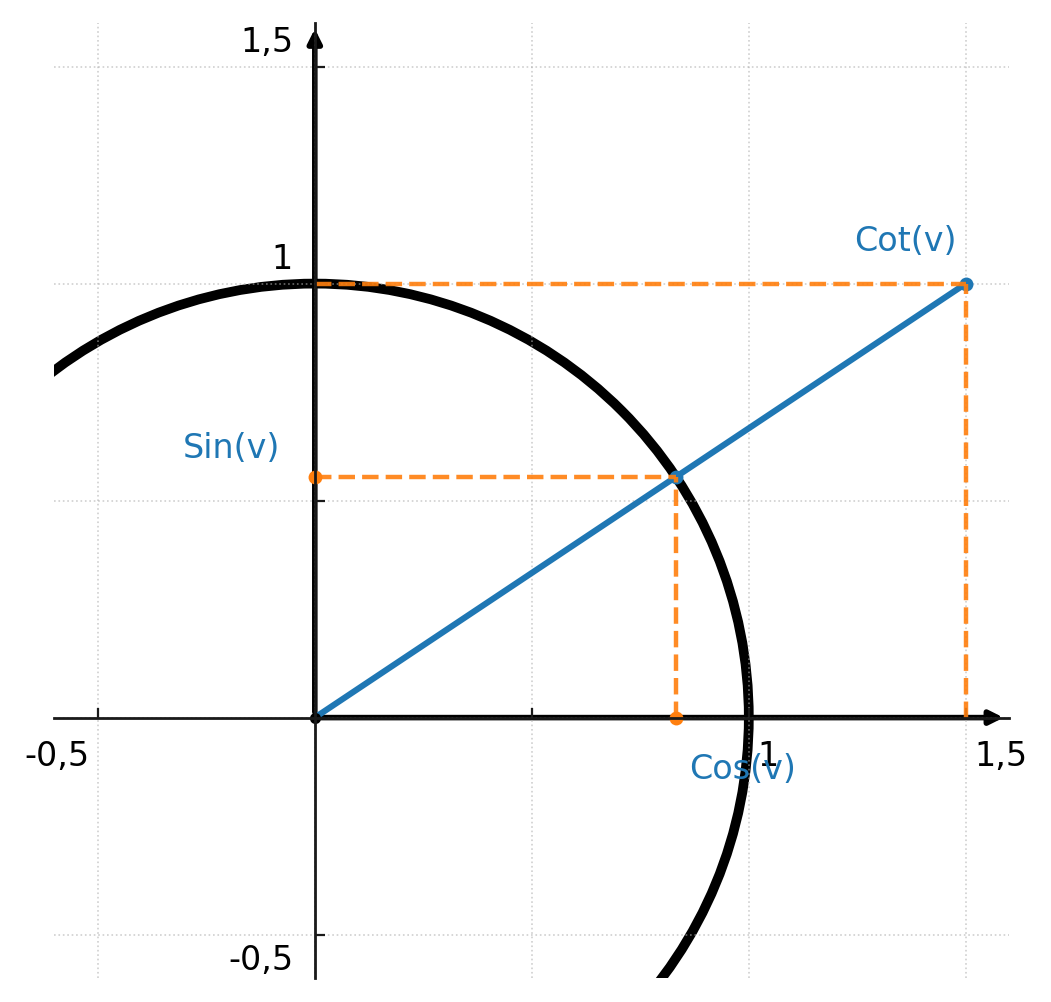
Vinklen på 25 grader regnes sådan her:

 

$$ cot(v) = \frac{cos(v)}{sin(v)} \qquad \Leftrightarrow $$

$$ cot(v) = \frac{cos(25^\circ)}{sin(25^\circ)} \qquad \Leftrightarrow $$

$$ cot(v) = \frac{0.906}{0.423} \qquad \Leftrightarrow $$

$$ cot(v) \approx 2.14 $$

 

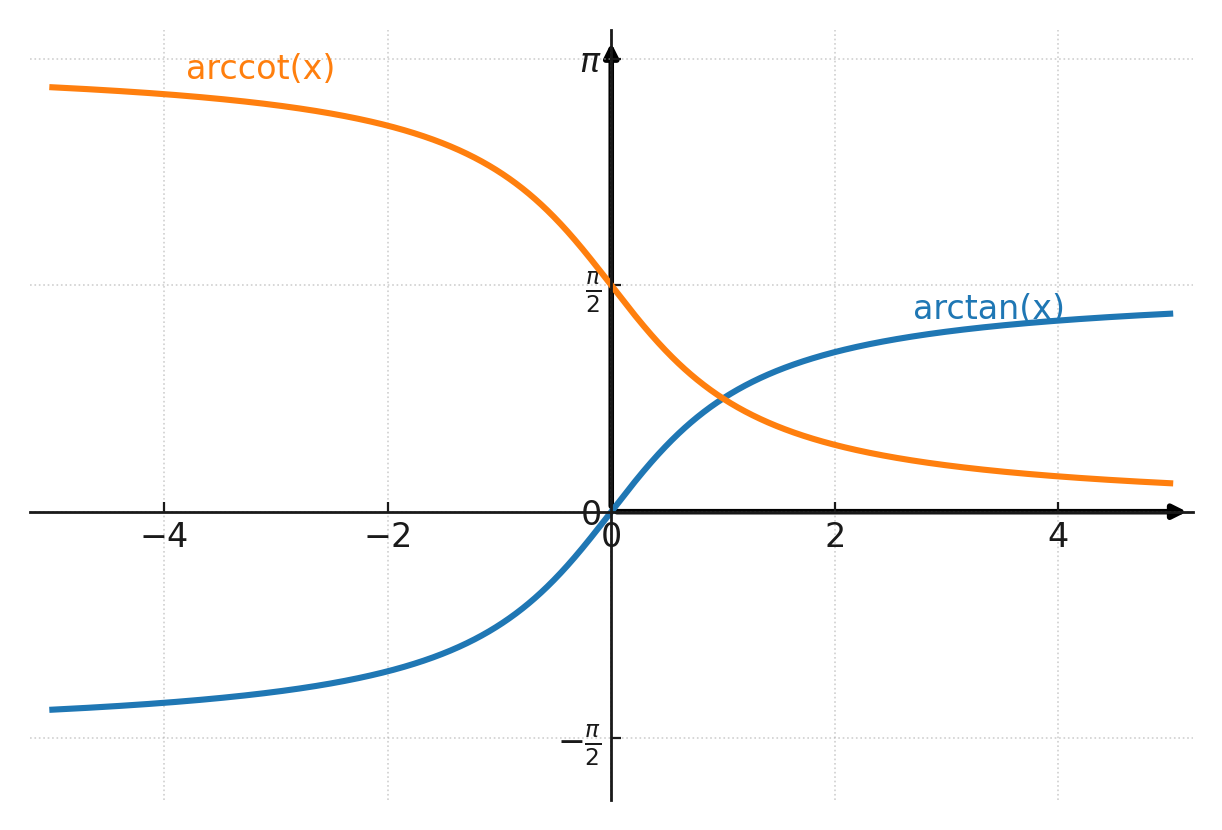
Inverse funktioner

Ligesom arcsin og arccos findes der også inverse funktioner til tangens og cotangens. Disse kaldes arctan og arccot (eller skrives som tan^-1 og cot^-1).

Hvis du kender tangens til en vinkel, men ikke selve vinklen, kan du finde den med arctan. For eksempel ved vi at:

 

$$ tan(45^\circ) = 1 $$

 

Dermed gælder også:

 

$$ tan^{-1}(1) = 45^\circ $$

 

Arctan kan bruges til at beregne en vinkel ud fra forholdet mellem to sider i en retvinklet trekant. 

 

Arccot fungerer på samme måde for cotangens. Hvis du kender cotangens til en vinkel, kan du finde vinklen med arccot. For eksempel:

 

$$ cot(45^\circ) = 1 \qquad \Leftrightarrow \qquad cot^{-1}(1) = 45^\circ $$

 

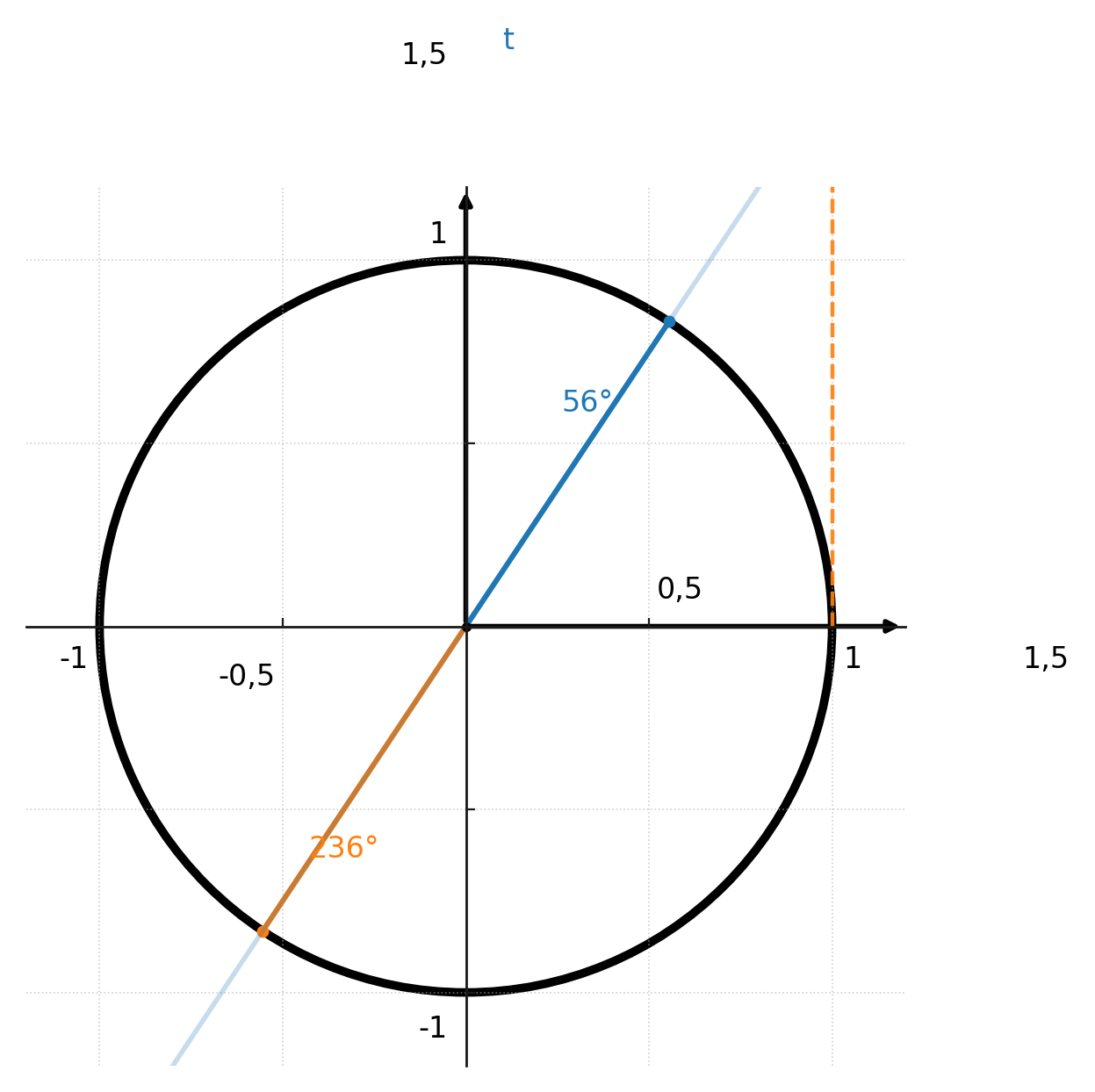
Begge funktioner vil give to løsninger, hvis ikke de begrænses. Her ses arctans to løsninger i første og tredie kvadrant:

 

 

Funktionerne er begrænset således

 

• For arctan begrænses vinklen til intervallet \(-90^\circ \leq v \leq 90^\circ\)
• For arccot begrænses vinklen til intervallet \(0^\circ \leq v \leq 180^\circ\)

 

Derved er funktionerne entydige!

 

De to inverse funktioner er tegnet ind i koordinatsystemet. Bemærk at y-aksen er i radianer og ikke grader.