Sinus og cosinus

Hvis du tegner en vinkel ind i enhedscirklen, kan du aflæse cosinus og sinus på enhedscirklens omkreds, som et punkt i koordinatsystemet.

Resultatet vil altid være mellem -1 og 1, fordi punktet altid ligger på cirklen med radius 1.

På figuren er en vinkel på 25 grader tegnet ind i enhedscirklen, og vi kan aflæse skæringspunktet på x- og y-aksen.

 

 

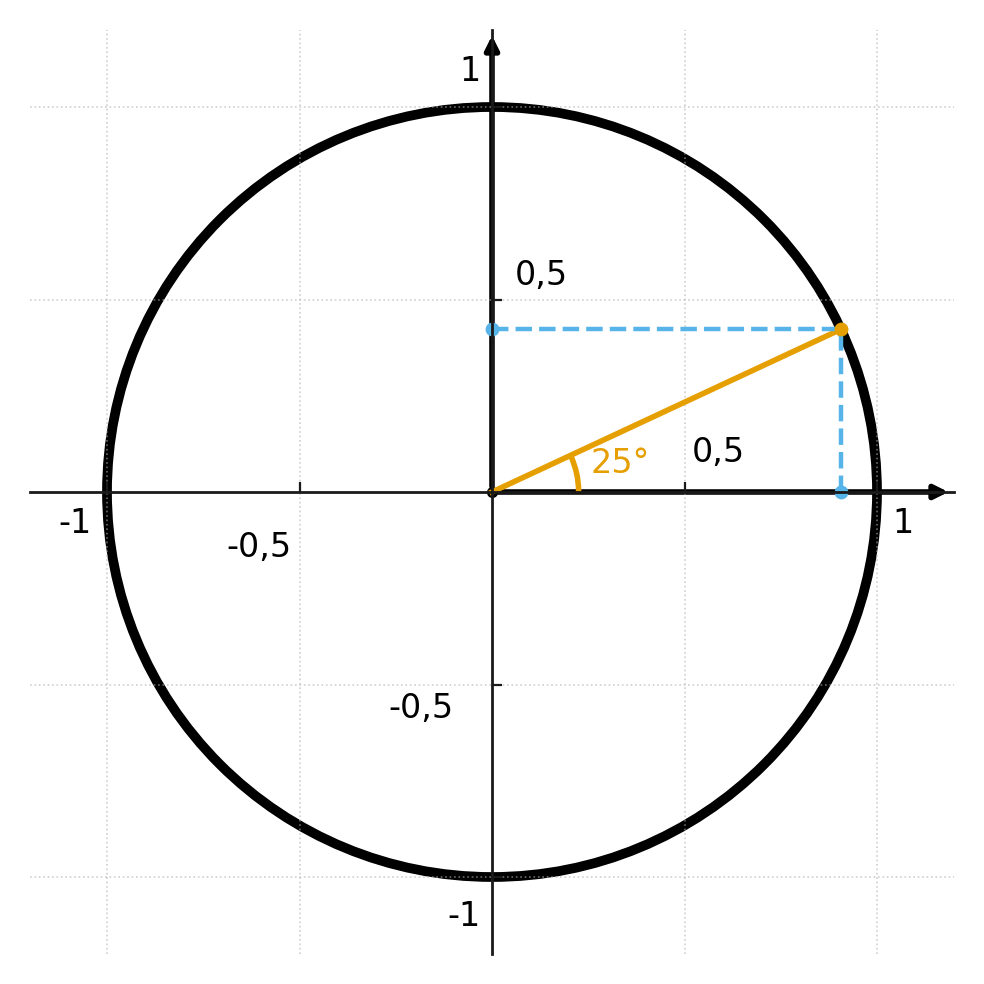
Husk at man altid aflæser koordinater som \( \large (x,y) \). Hvilket svarer til \( \large (cosinus, sinus) \).

Cosinus og sinus er altså koordinatsættet til retningspunktet – det punkt, hvor vinklen rammer enhedscirklen.

Vinklen på figuren er 25 grader, og hvis man kunne aflæse det præcist nok, ville man se at:

 

$$ sin(v) \approx 0,906 $$

$$ cos(v) \approx 0,423 $$

 

Det er selvfølgelig ikke muligt at aflæse nøjagtigt på enhedscirklen, og man vil normalt bruge cosinus- og sinus-knapperne på lommeregneren.

 

Inverse funktioner

Hvis du kender cosinus eller sinus til en vinkel, men ikke selve vinklen, kan du regne den anden vej med de inverse funktioner. Disse kaldes arccos og arcsin (eller skrives som cos^-1 og sin^-1).

De inverse funktioner findes også på en lommeregner, som regel på samme tast som de almindelige funktioner.

 

Lad os antage at du ved at cos(A) = 0,906, men du ikke kender vinklen. Så kan du finde den ved:

 

$$ cos^{-1}(0,906) \approx 25^\circ $$

 

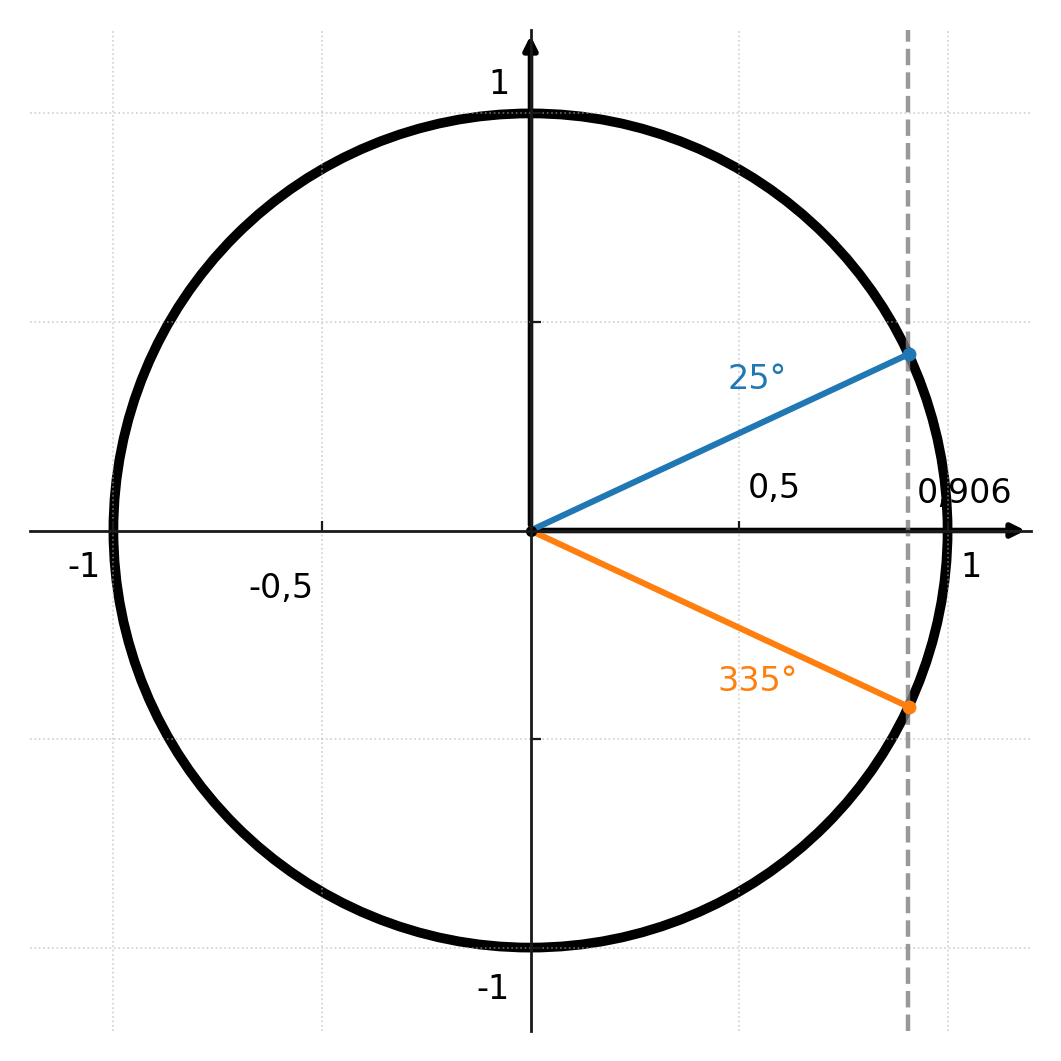
Bemærk at de inverse funktioner ikke altid giver en entydig løsning. For eksempel kan cos(v) = 0,906 både gælde for en vinkel på 25° og for en vinkel på 335° (-25°).

For at kunne bruge funktionerne som entydige inverse funktioner begrænser man deres definition:

 

• Arccos er normalt begrænset til intervallet \(0^\circ \leq v \leq 180^\circ\) (\(0 \leq v \leq \pi\) rad)
• Arcsin er normalt begrænset til intervallet \(-90^\circ \leq v \leq 90^\circ\) (\(-\tfrac{\pi}{2} \leq v \leq \tfrac{\pi}{2}\) rad)

 

Det betyder, at løsningen på 335° ikke kommer med, og at arcsin altid returnerer vinkler i første eller fjerde kvadrant.

 

 

 

 

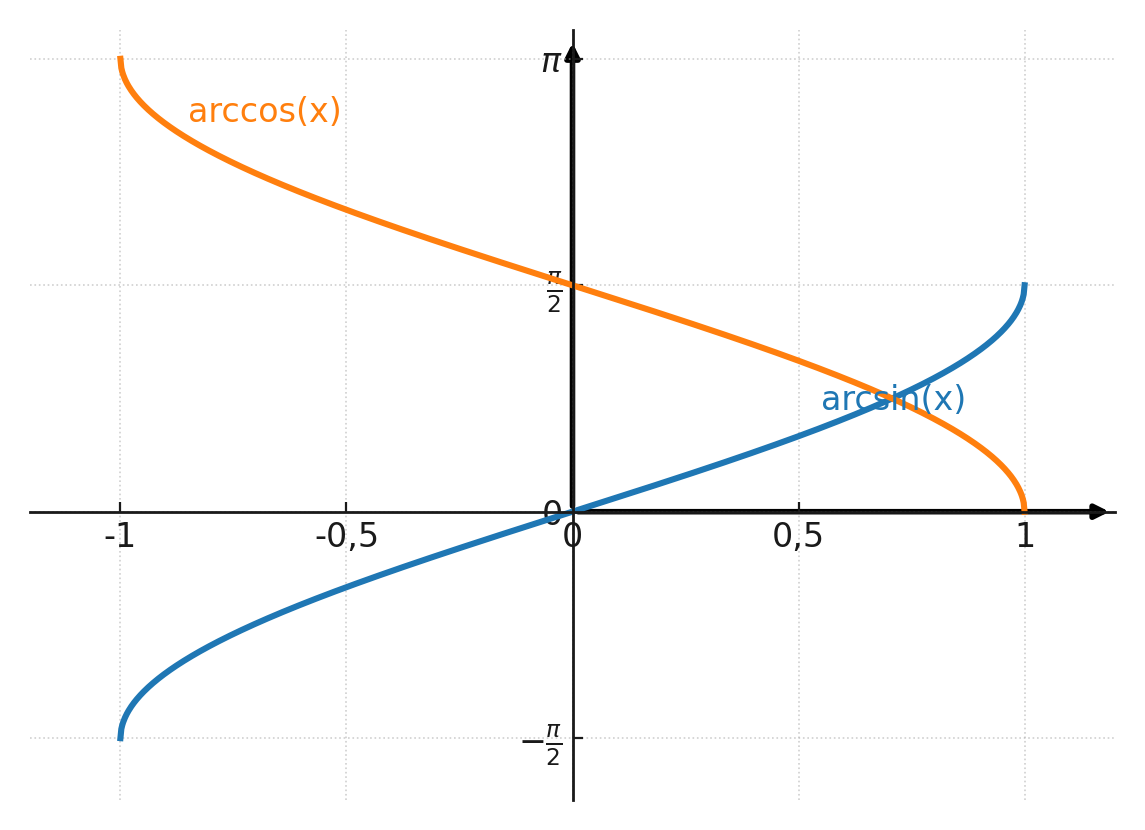
De to inverse er funktioner tegnet ind i koordinatsystem. Bemærk at y-aksen er i radianer og ikke grader.

Hvis man aflæser på arccos kurven ved x = 0,906, så rammer man 0,44 rad hvilket svarer til 25°

 

 

 

Radianer og Grader

For at konvertere mellem radianer og grader bruger man formlen:

 

$$ \text{grader} = \text{radianer} \cdot \frac{180^\circ}{\pi} $$

$$ \text{radianer} = \text{grader} \cdot \frac{\pi}{180^\circ} $$

 

Eksempel:

 

$$ 0,44 \,\text{rad} \approx 0,44 \cdot \tfrac{180^\circ}{\pi} \approx 25^\circ $$