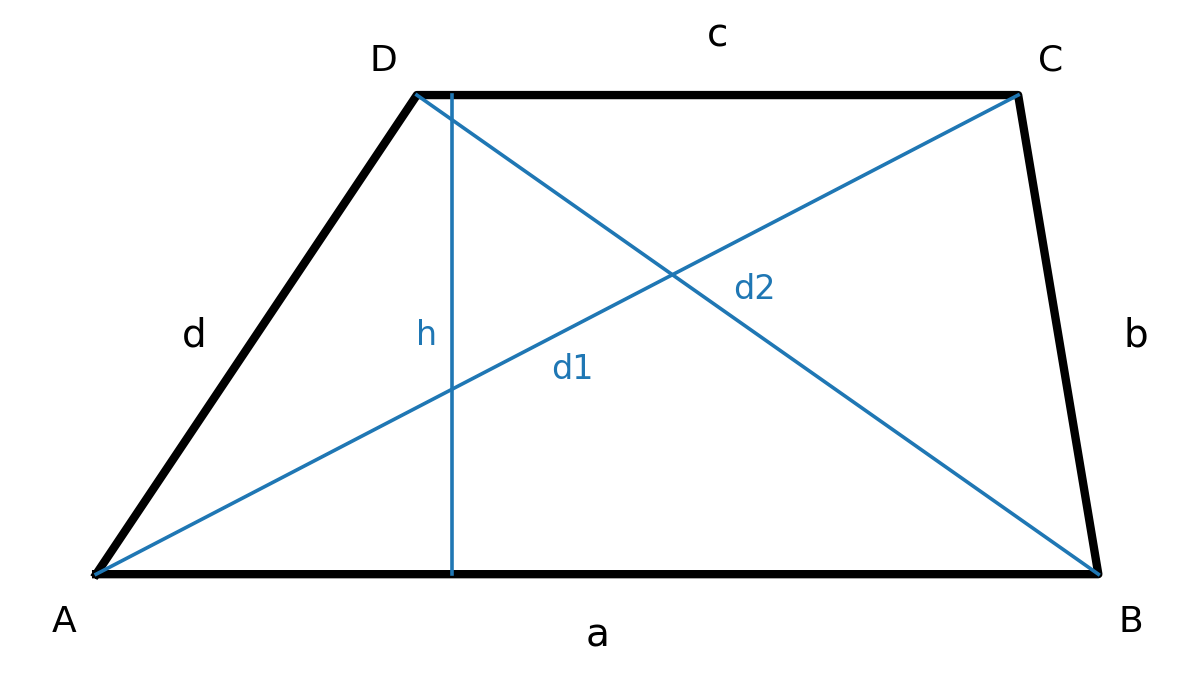
Trapez
En trapez er en firkant, hvor to af siderne er parallelle. De parallelle sider kaldes for grundlinjer.
Hvis de to andre sider også er parallelle, er figuren et parallelogram. De sider, der ikke er parallelle, kaldes ben.
Varianter
Ligebenet trapez: \(b=d\). Basisvinkler ved hver grundlinje er parvist lige store, og diagonalerne er lige lange.
Retvinklet trapez: To af vinklerne er rette.
Egenskaber
- Summen af de indre vinkler er 360°.
- Langs hvert ben gælder \( \angle A + \angle D = 180^\circ \) og \( \angle B + \angle C = 180^\circ \) (parallellitet).
- Midtlinjen (linjen mellem benenes midtpunkter) har længden \( m=\tfrac{a+c}{2} \), og arealet kan skrives \( A=m\cdot h \).
Areal og omkreds
Standardformlen for arealet:
$$ \large A=\tfrac{h}{2}\,(a+c) $$
Hvis basisvinklerne ved \(A\) og \(B\) kendes, kan benenes længder skrives som \( d=\tfrac{h}{\sin(\angle A)} \) og \( b=\tfrac{h}{\sin(\angle B)} \). Dermed bliver omkredsen:
$$ \large P = (a+c) + h\!\left(\tfrac{1}{\sin(\angle A)}+\tfrac{1}{\sin(\angle B)}\right) $$
Areal ud fra fire sider
Kendes alle fire sider, kan højden og dermed arealet findes uden vinkler:
$$ \large A = \tfrac{1}{2}(a+c)\,\sqrt{\,b^2 - \Bigl(\tfrac{(a-c)^2 + b^2 - d^2}{2(a-c)}\Bigr)^2} $$
Her antages \(a \ne c\). For et parallelogram tager man grænsen \(a \to c\).
Diagonaler
Diagonalerne fås med cosinusrelationen i de tilhørende trekanter:
$$ \large d_1 = \sqrt{a^2 + b^2 - 2ab\cos(\angle B)} $$
$$ \large d_1 = \sqrt{c^2 + d^2 - 2cd\cos(\angle D)} $$
$$ \large d_2 = \sqrt{a^2 + d^2 - 2ad\cos(\angle A)} $$
$$ \large d_2 = \sqrt{b^2 + c^2 - 2bc\cos(\angle C)} $$
I en ligebenet trapez gælder \(d_1=d_2\).
Omskreven cirkel
Kun ligebenede trapezer kan indskrives i en cirkel. Ækvivalent gælder de modsatte vinkelsummer:
- \(\angle A + \angle C = 180^\circ\)
- \(\angle B + \angle D = 180^\circ\)
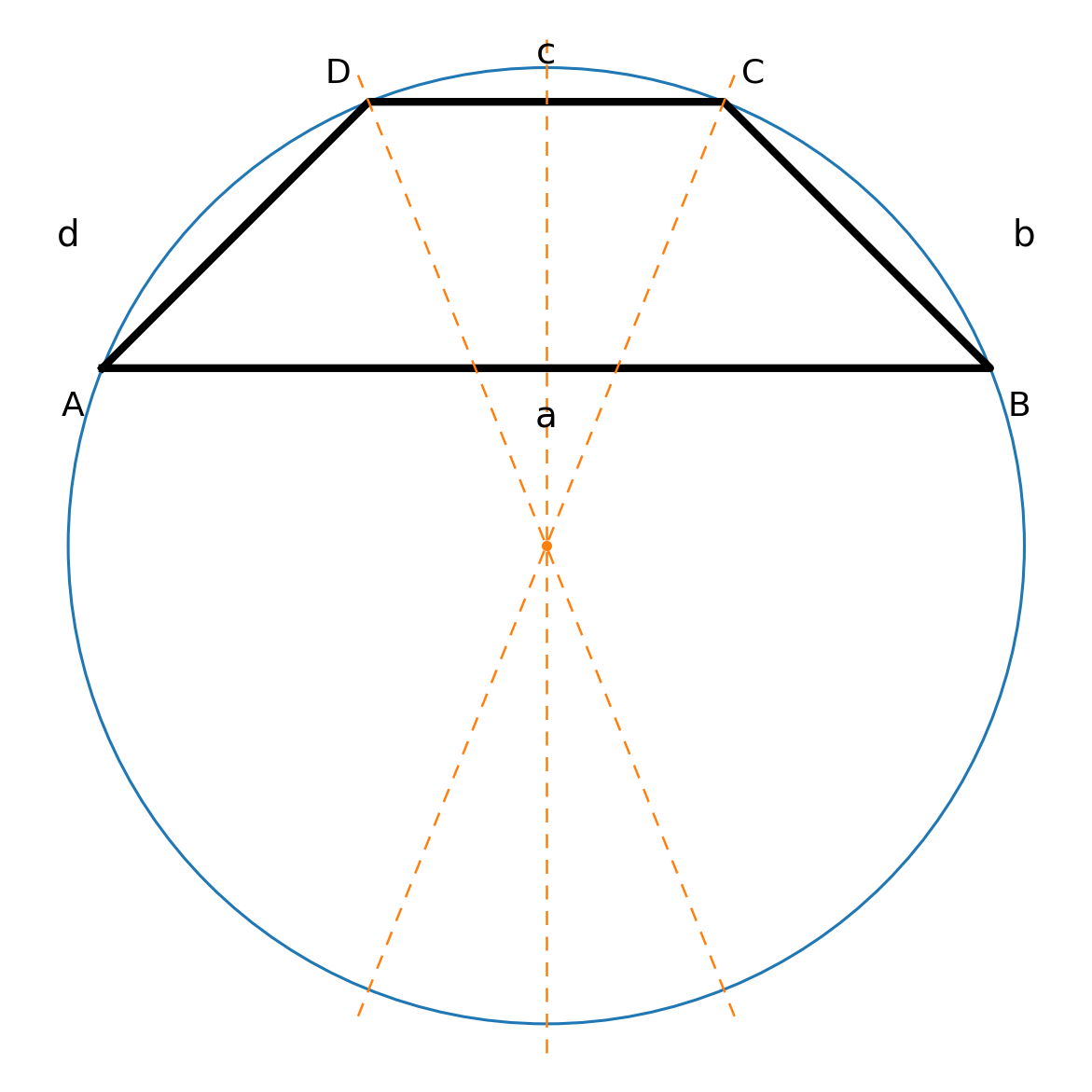
Centrum for cirklen kan findes ved at tegne vinkelhalveringslinjer ud fra vinkel C og D, og eventuelt også midtnormalen for side a og c (symmetriaksen)
Bemærk at for enhver trapez gælder \( \angle A + \angle D = 180^\circ \) og \( \angle B + \angle C = 180^\circ \) som følge af parallelle linjer. Det gør den ikke cyklisk i sig selv.
Indskreven cirkel
En trapez har en indskreven cirkel, som tangerer alle fire sider, hvis og kun hvis:
$$ \large a + c = b + d $$
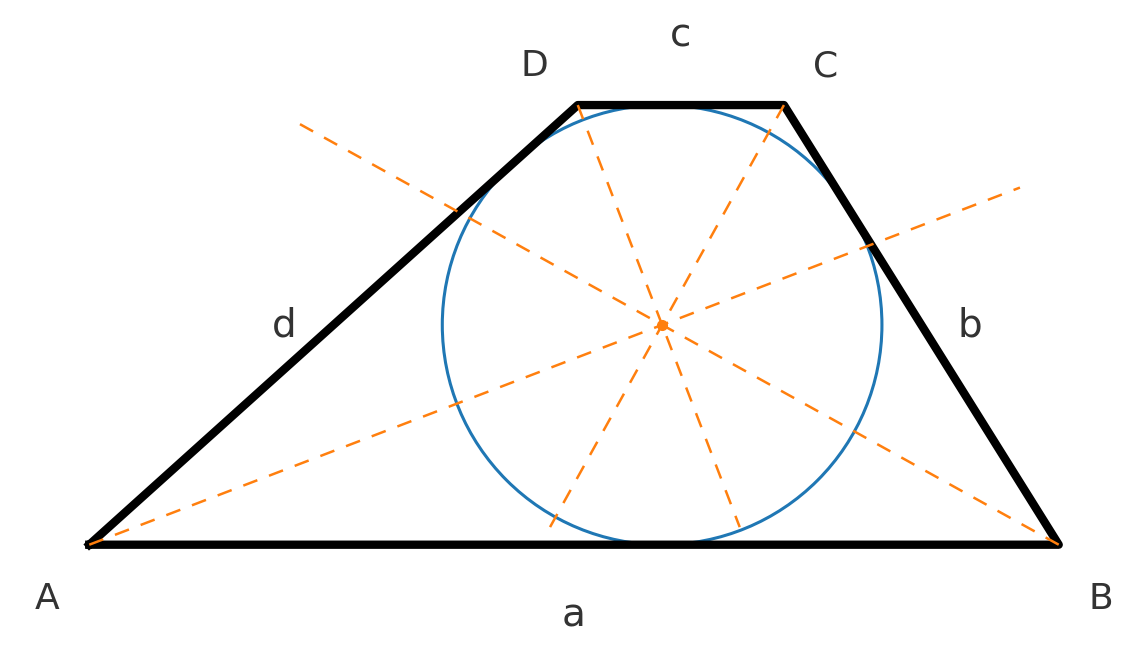
Centrum for cirklen kan findes ved at tegne vinkelhalveringslinjer ud fra de fire vinkler.
For tangentiale firkanter gælder i øvrigt \( A = r \cdot s \), hvor \( r \) er indradius og \( s \) er halvomkredsen.
Anvendelser
- Opdeling i to retvinklede trekanter plus et rektangel gør konstruktioner og trigonometriske beregninger overskuelige.
- Trapezmetoden bruges til numerisk approksimation af integraler.