Parallelogram
Et parallelogram er en firkant, hvor de modstående sider er lige lange og parallelle.
Figuren kan opfattes som et “skævt rektangel”.
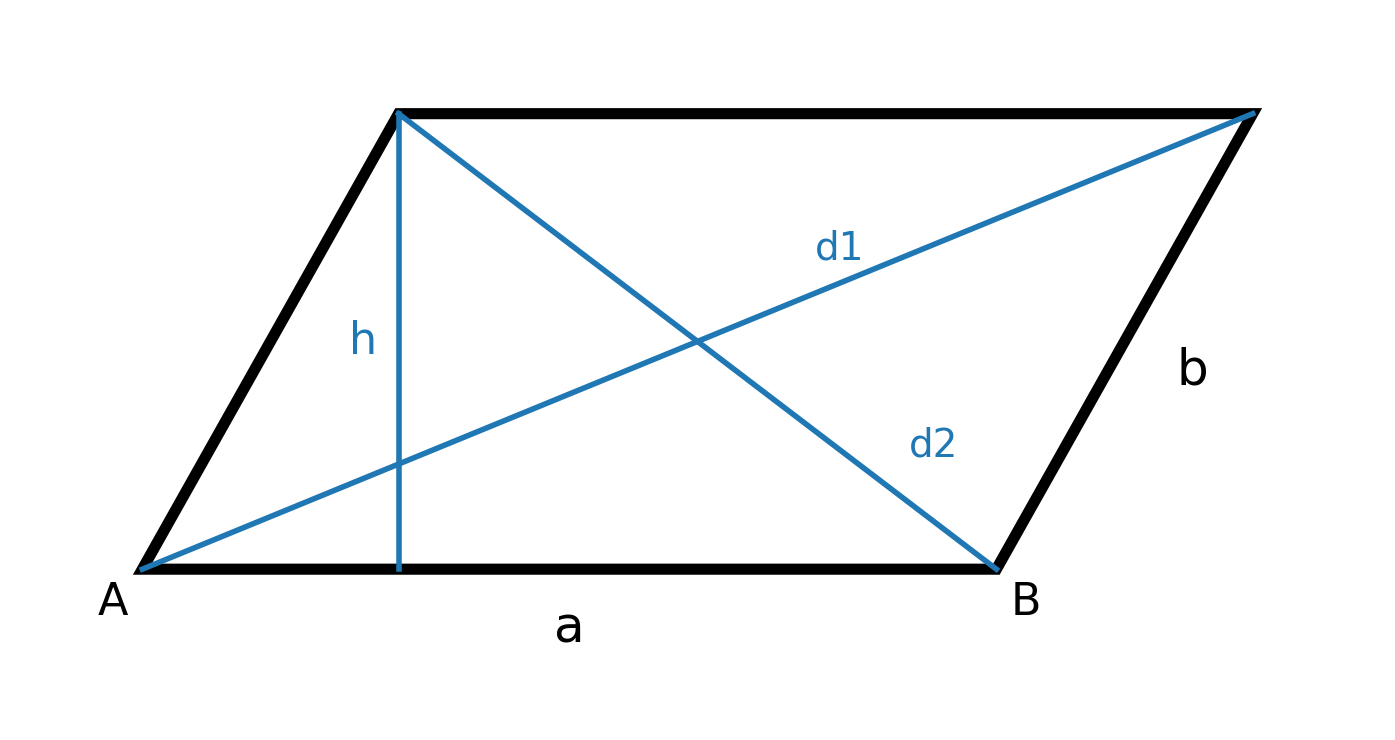
Der er ingen rette vinkler i et parallelogram, men vinklerne overfor hinanden er altid lige store. Summen af to nabovinkler er 180°.
$$ \large \angle A + \angle B = 180^\circ $$
En særlig variation af parallelogrammet kaldes en rombe. Her er alle fire sider lige lange. På samme måde som et ligesidet rektangel kaldes et kvadrat.
Diagonalernes skæringspunkt i et parallelogram er samtidig deres halveringspunkt.
Det betyder, at diagonalerne deler hinanden i to lige store dele, men de står ikke nødvendigvis vinkelret på hinanden.
Egenskaber, der kendetegner et parallelogram
- Modstående sider er lige lange.
- Modstående sider er parallelle.
- Modstående vinkler er lige store.
- Nabovinkler danner tilsammen 180°.
- Diagonalernes skæringspunkt er også deres halveringspunkt.
- Et parallelogram kan opdeles i to kongruente trekanter langs en diagonal.
Når man skal regne på et parallelogram, er det ofte nødvendigt at bruge trigonometri og beregninger med trekanter.