Rombe

En rombe er et skævt kvadrat og minder meget om et parallelogram, som er et skævt rektangel.

Man kan også sige, at alle kvadrater er romber, men ikke alle romber er kvadrater, fordi vinklerne i en rombe ikke behøver at være 90 grader.

Romben er ofte nem at regne på i praksis, fordi alle sider er lige lange ligesom i et kvadrat.

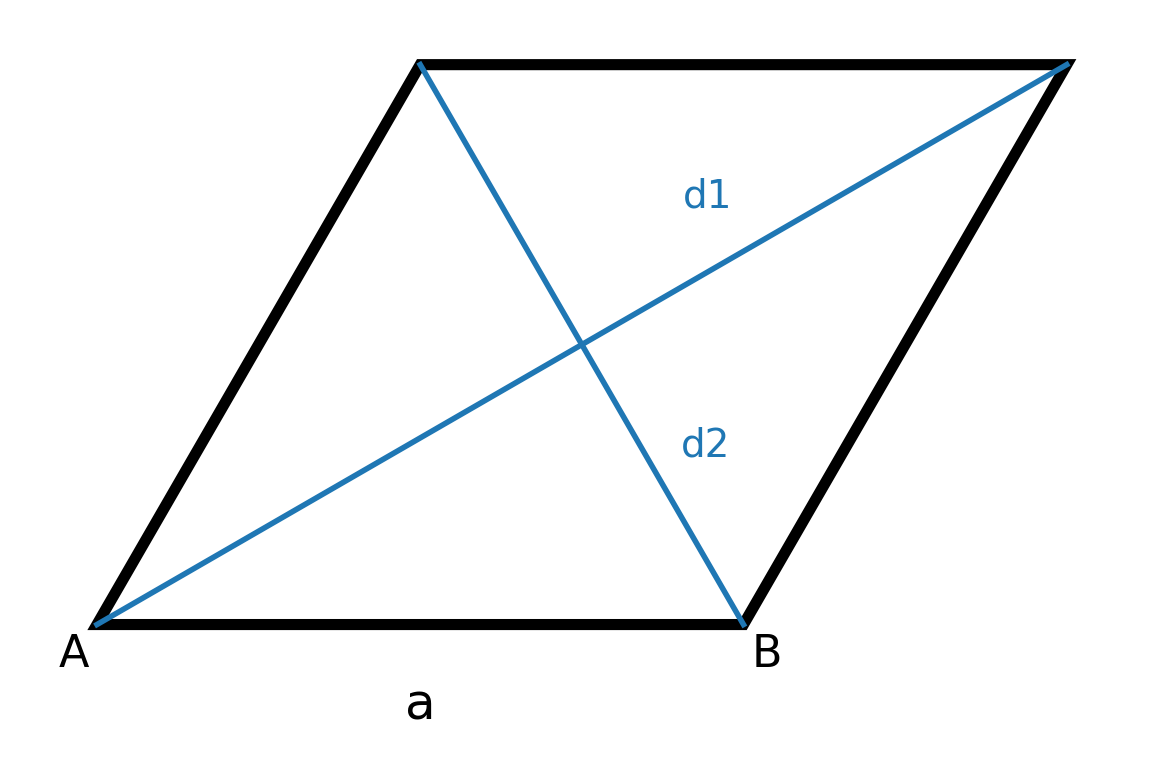
Rombe

Alle fire sider er lige lange.
Modstående sider er parallelle.
Modstående vinkler er lige store, og nabovinkler danner tilsammen 180 grader.
Diagonalernes skæringspunkt er også deres halveringspunkt.
Diagonalernes retninger står vinkelret på hinanden.
Hver diagonal halverer de tilstødende vinkler, så figuren har to akser for spejlsymmetri langs diagonalerne.
Romben kan opdeles i fire kongruente retvinklede trekanter.

At diagonalerne halverer hinanden og står vinkelret betyder, at man kan opdele romben i retvinklede trekanter.

Dermed kan man bruge Pythagoras læresætning og elementær trigonometri i beregninger.

Regnemaskine

$$ a=\frac{d_2}{sin\bigl(\frac{A}{2}\bigr)\cdot 2} $$

$$ a=\frac{d_1}{cos\bigl(\frac{A}{2}\bigr)\cdot 2} $$

$$ a = \frac{1}{2}\sqrt{d_1^2 + d_2^2} $$

$$ d_1=\frac{2 \cdot Area}{d_2} $$

$$ d_1=2a \cdot sin\biggl(\frac{\angle B}{2}\biggr) $$

$$ d_1=2a \cdot cos\biggl(\frac{\angle A}{2}\biggr) $$

$$ d_2=\frac{2 \cdot Area}{d_1} $$

$$ d_2=2a\cdot cos\biggl(\frac{\angle B}{2}\biggr) $$

$$ d_2=2a \cdot sin\biggl(\frac{\angle A}{2}\biggr) $$

$$ A=\frac{1}{2} \cdot d_1\cdot d_2 $$

$$ A= a^2 \cdot sin(A) $$

$$ P=4\cdot a $$

$$ P= 2 \cdot \sqrt{d_1^2 + d_2^2} $$

$$ B=2\cdot cos^{-1}\biggl(\frac{d_2}{2\cdot a}\biggr) $$

$$ B=2\cdot sin^{-1}\biggl(\frac{d_1}{2\cdot a}\biggr) $$

$$ B=2\cdot tan^{-1}\biggl(\frac{d_1}{d_2}\biggr) $$

$$ A=2\cdot sin^{-1}\biggl(\frac{d_2}{2\cdot a}\biggr) $$

$$ A=2\cdot cos^{-1}\biggl(\frac{d_1}{2\cdot a}\biggr) $$

$$ A=2\cdot tan^{-1}\biggl(\frac{d_2}{d_1}\biggr) $$