Kartesisches Produkt in zwei und mehreren Dimensionen
Das kartesische Produkt ist eine Möglichkeit, Mengen zu kombinieren, um geordnete Paare oder Tupel zu bilden. Der Name stammt von dem französischen Mathematiker René Descartes (lateinisch: Cartesius), weil das Konzept die Grundlage für Koordinatensysteme und die geometrische Darstellung von Punkten bildet.
Kartesisches Produkt zweier Mengen
Wenn wir zwei Mengen \( \large A\) und \( \large B\) haben, ist ihr kartesisches Produkt die Menge aller geordneten Paare, wobei das erste Element aus \( \large A\) und das zweite Element aus \( \large B\) stammt:
$$ \large A \times B = \{(a,b) \mid a \in A, \; b \in B\} $$
Beispiel: Sei \( \large A = \{1,2\}\) und \( \large B = \{x,y\}\). Dann gilt:
$$ \large A \times B = \{(1,x), (1,y), (2,x), (2,y)\} $$
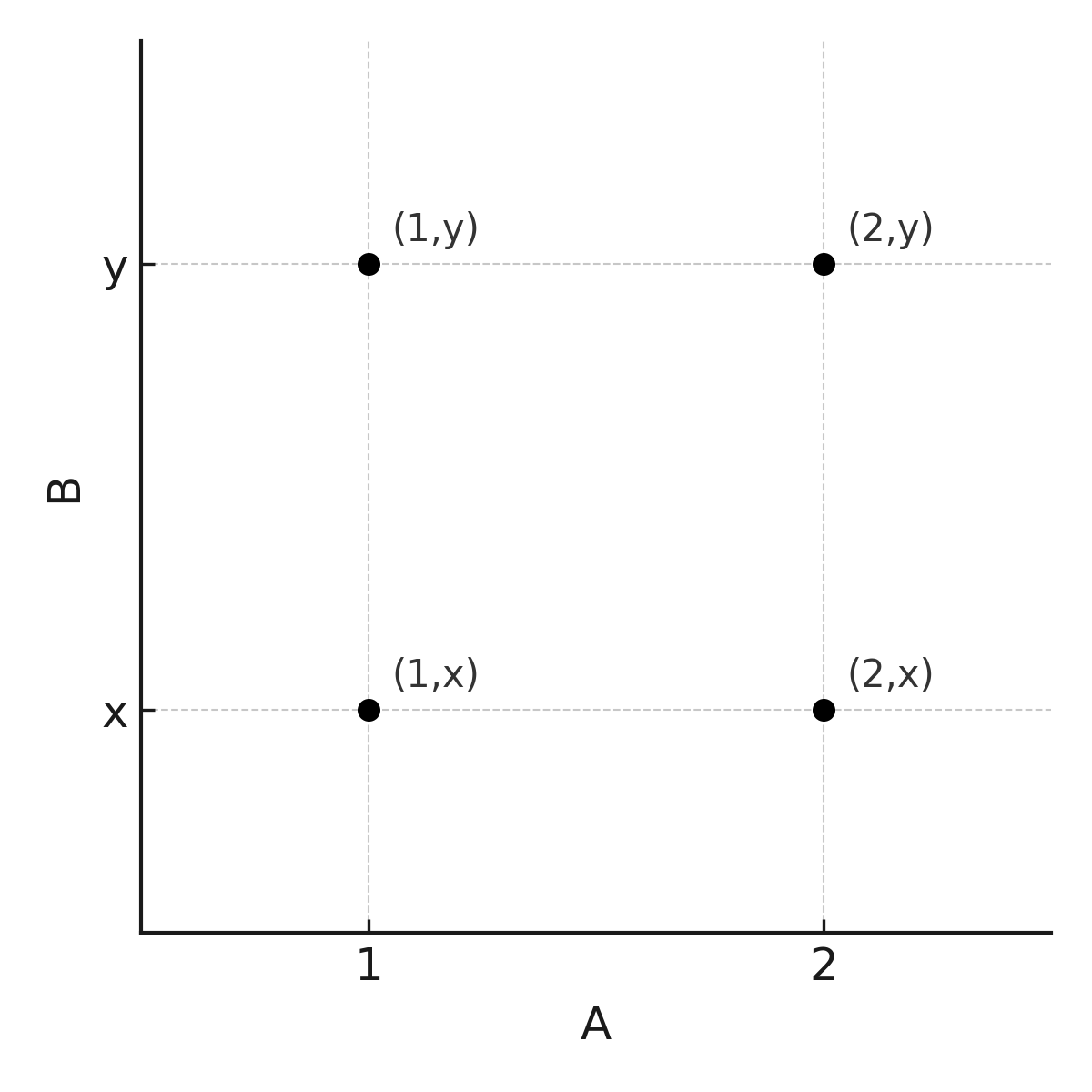
Hinweis: Die Reihenfolge spielt eine Rolle. Die Menge \( \large B \times A\) ist:
$$ \large B \times A = \{(x,1),(x,2),(y,1),(y,2)\} $$
Also gilt im Allgemeinen: \( \large A \times B \neq B \times A\).
Die Kardinalität (Anzahl der Elemente) des Produkts wird durch bestimmt:
$$ \large |A \times B| = |A| \cdot |B| $$
Beispiel: Wenn \( \large |A|=3\) und \( \large |B|=4\), dann enthält \( \large A \times B\) \( \large 3 \cdot 4 = 12\) geordnete Paare.
Kartesisches Produkt in höheren Dimensionen
Die Idee kann auf drei oder mehr Mengen erweitert werden. Für drei Mengen wird es definiert als:
$$ \large A \times B \times C = \{(a,b,c) \mid a \in A, \; b \in B, \; c \in C\} $$
Beispiel: Wenn \( \large A = \{1,2\}, B = \{x\}, C = \{p,q\}\), dann gilt:
$$ \large A \times B \times C = \{(1,x,p), (1,x,q), (2,x,p), (2,x,q)\} $$
Allgemein kann man ein kartesisches Produkt von \( \large n\) Mengen definieren, das alle \( \large n\)-Tupel enthält, bei denen jedes Element aus einer der Mengen stammt. Wenn alle Mengen gleich sind, zum Beispiel \( \large A \times A \times \cdots \times A\) (mit \( \large n\) Wiederholungen), wird dies als \( \large A^n\) geschrieben.
Beispiele:
- \( \large \mathbb{R}^2\): alle Punkte in der Ebene, geschrieben als \((x,y)\).
- \( \large \mathbb{R}^3\): alle Punkte im Raum, geschrieben als \((x,y,z)\).
- \( \large \{0,1\}^3\): alle binären Tripel, d. h. \( \large (0,0,0),(0,0,1),\ldots,(1,1,1)\).
Die Anzahl der Elemente in einem kartesischen Produkt endlicher Mengen ist:
$$ \large |A_1 \times A_2 \times \cdots \times A_n| = |A_1| \cdot |A_2| \cdot \ldots \cdot |A_n| $$
Bedeutung und Anwendungen
Kartesische Produkte bieten eine systematische Möglichkeit, neue Strukturen aus bekannten Mengen zu bilden.
Sie bilden die Grundlage für:
- Koordinatensysteme in Mathematik und Geometrie.
- Tabellen und Datenstrukturen in der Informatik.
- Relationen zwischen Objekten (z. B. Graphen).