Unechte Brüche und gemischte Zahlen

Was sind unechte Brüche

Ein Bruch wird unecht genannt, wenn der Zähler größer ist als der Nenner. Zum Beispiel: \(\large \frac{9}{8}\) 

 

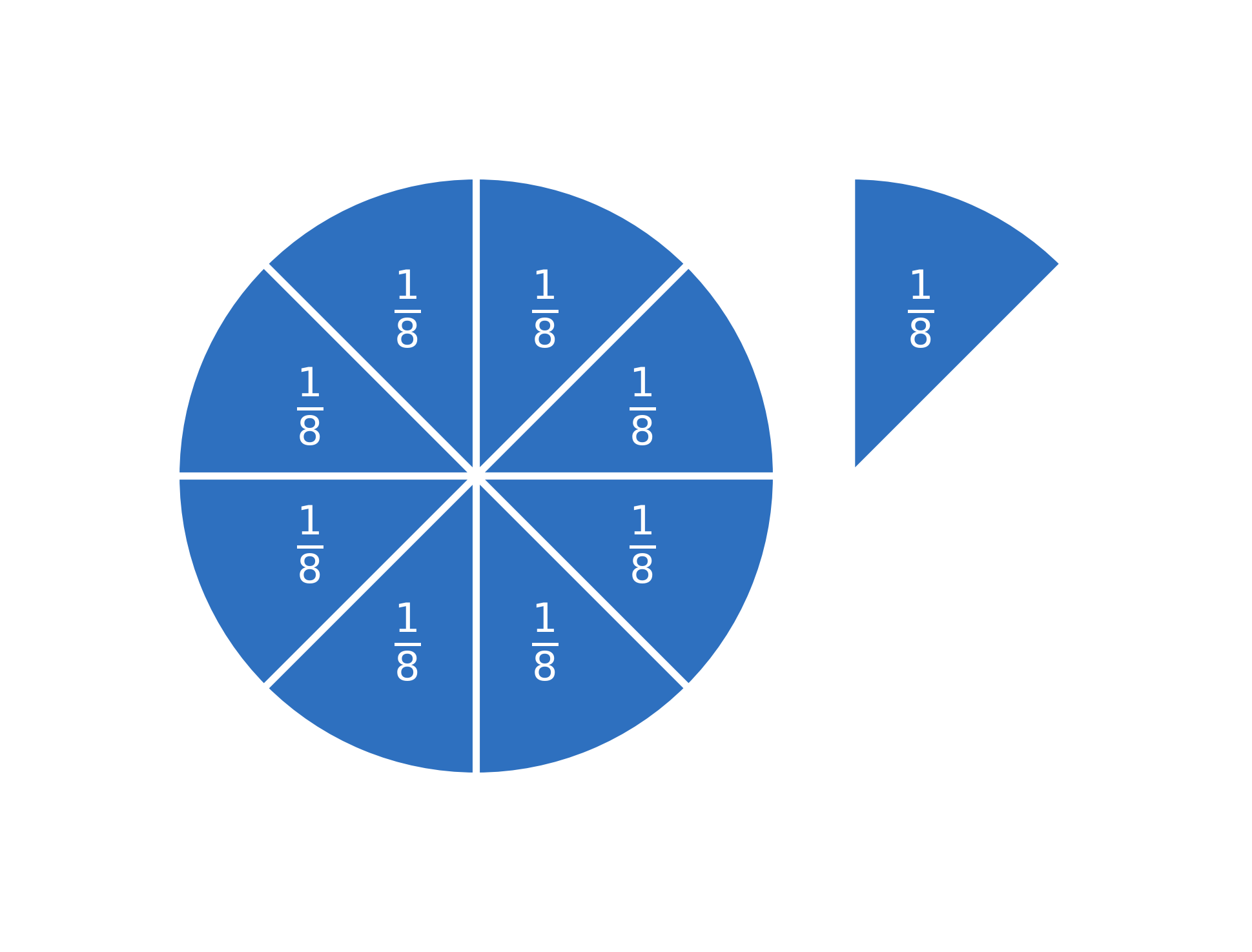
Wenn du dich an unsere Pizza erinnerst, weißt du, dass \(\large \frac{8}{8}\)  einer ganzen Pizza entspricht.

Das bedeutet, dass  \(\large \frac{9}{8}\)  gleichbedeutend ist mit einer ganzen Pizza + einem zusätzlichen Stück, weil: 

 

$$ \large \frac{9}{8} \Leftrightarrow \frac{8}{8} + \frac{1}{8} $$

 

Man kann es auch so schreiben:

 

$$ \large 1+\frac{1}{8} = 1\frac{1}{8} $$

 

Ein weiteres Beispiel: \(\large \frac{15}{7}\) ist ein unechter Bruch. Er kann so geschrieben werden: \(\large 2\frac{1}{7}\)

 

 

Gemischte Zahlen

Wenn du \(\large 1+\frac{1}{8}\ \) schreibst, kannst du das Pluszeichen weglassen, sodass nur noch \(\large 1\frac{1}{8}\ \) steht

Das nennt man eine gemischte Zahl, weil sie sowohl aus ganzen Zahlen als auch aus Brüchen besteht.

 

Gemischte Zahlen werden beim Rechnen oft in unechte Brüche umgeschrieben:

$$ \large 2\frac{1}{7} = \frac{15}{7} $$

 

Es ist nämlich einfacher, unechte Brüche zu multiplizieren und zu dividieren als gemischte Zahlen.

 

Du kannst dieselben Rechenregeln auf unechte Brüche anwenden wie auf echte Brüche.

Du musst nur daran denken, dass du keinen unechten Bruch als Ergebnis einer Aufgabe abgeben darfst. Er muss in eine gemischte Zahl oder eine ganze Zahl umgewandelt werden.

 

 

Ganze Zahlen als Brüche

Alle ganzen Zahlen können als Brüche geschrieben werden. Du weißt schon, dass \(\large \frac{8}{8}=1\ \). Dasselbe gilt für \(\large \frac{1}{1}=1\ \) 

 

Das bedeutet, dass \(\large 2=\frac{2}{1}\ \) 

 

Die Regel lautet so: \(\large a=\frac{a}{1}\ \) 

 

Aber man kann auch schreiben \(\large 4=\frac{8}{2}\ \). Das ist einfach eine Erweiterung von \(\large \frac{4}{1}\ \) , wobei Zähler und Nenner mit 2 multipliziert wurden. 

 

Ein Bruch ist auch eine Division.

Da steht: 8 geteilt durch 2 und das ist gleich 4.