Kontinuitet
Når man taler om funktioners adfærd, er et af de vigtigste begreber kontinuitet. Kontinuitet beskriver, om en funktion ændrer sig jævnt, eller om der opstår spring, huller eller bratte ændringer i grafen. En kontinuert funktion kan tegnes uden at løfte blyanten fra papiret.
Definition af kontinuitet
En funktion \( \large f(x) \) er kontinuert i et punkt \( \large x = a \), hvis grænseværdien for funktionen i dette punkt er lig med funktionens værdi. Det skrives som:
$$ \large \lim_{x \to a} f(x) = f(a) $$
For at en funktion skal være kontinuert i et punkt, skal tre betingelser være opfyldt:
- Funktionen er defineret i punktet \( \large a \)
- Grænseværdien \( \large \lim_{x \to a} f(x) \) eksisterer
- De to værdier er ens
Hvis bare én af disse betingelser ikke er opfyldt, er funktionen ikke kontinuert i punktet.
Typer af diskontinuitet
Der findes flere forskellige måder, hvorpå en funktion kan være ikke-kontinuert (diskontinuert). De vigtigste typer er:
| Type | Beskrivelse |
|---|---|
| Springdiskontinuitet | Funktionen hopper pludselig fra én værdi til en anden. |
| Hul | Grænseværdien eksisterer, men funktionen er ikke defineret i punktet. |
| Uendelig diskontinuitet | Funktionen vokser uden grænse i punktet (f.eks. ved en lodret asymptote). |
Disse typer kan tydeligt ses på grafen og hjælper med at forstå funktionens overordnede adfærd. Eksemplet herunder viser en springdiskontinuitet:
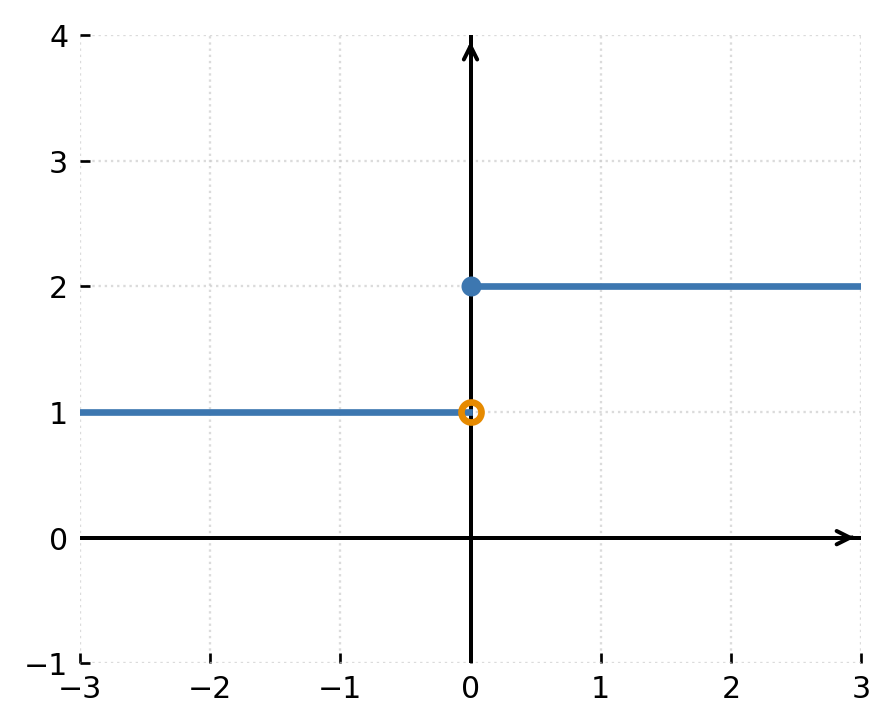
Eksempler
1: Funktionen \( \large f(x) = 2x + 1 \) er kontinuert overalt, fordi man frit kan sætte enhver værdi af x ind uden at bryde grafen.
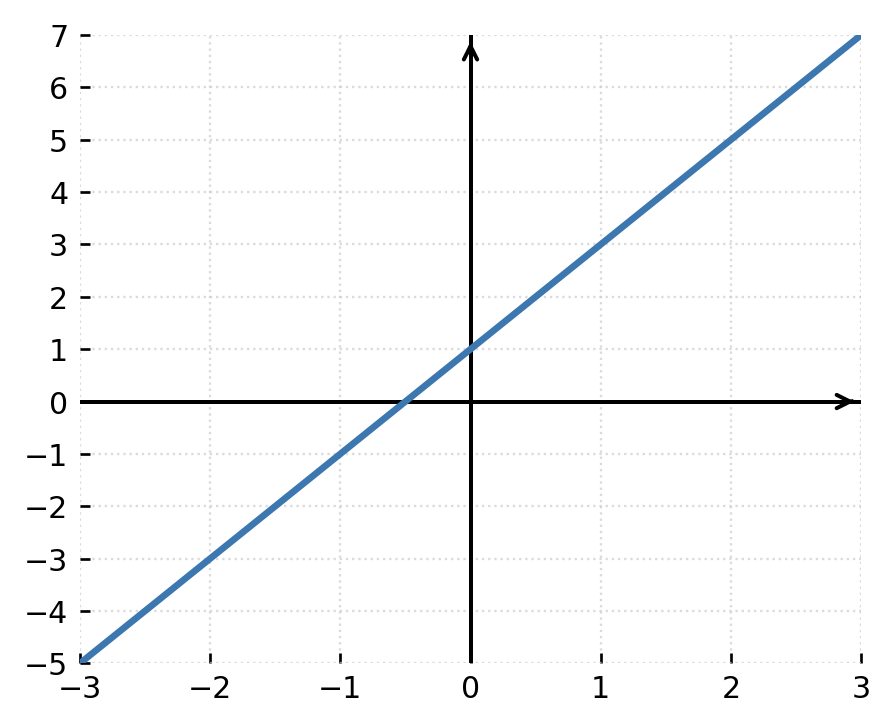
2: Funktionen
$$ \large f(x) = \frac{x^2 - 9}{x - 3} $$
er ikke defineret i \( \large x = 3 \), men grænseværdien i punktet eksisterer:
$$ \large \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = 6 $$
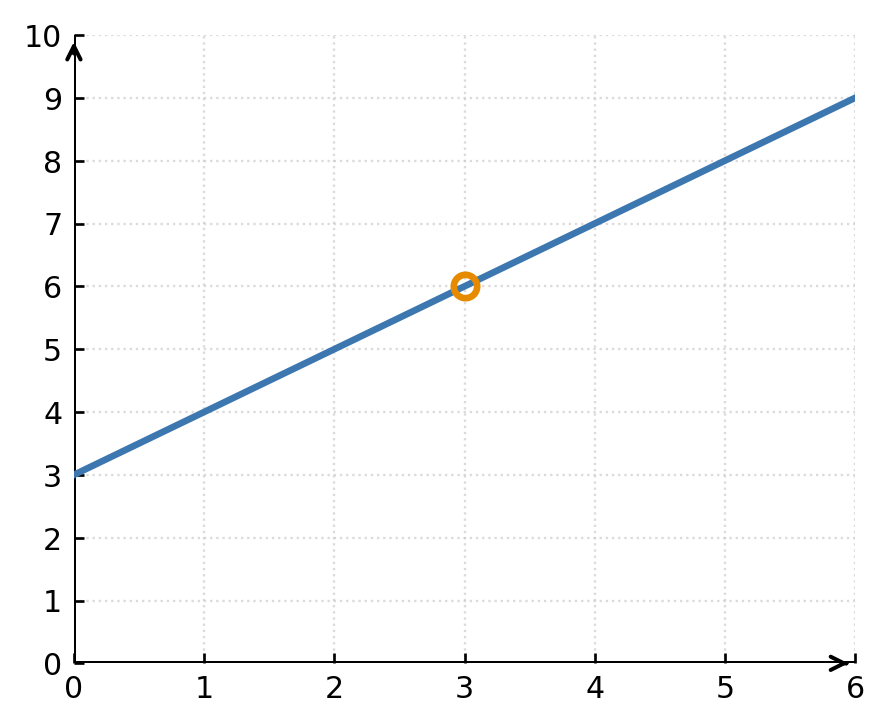
Grafen har derfor et hul i punktet (3, 6). Funktionen kan gøres kontinuert ved at definere \( \large f(3) = 6 \).
Kontinuitet i et interval
En funktion siges at være kontinuert på et interval, hvis den er kontinuert i hvert punkt i intervallet. Polynomier, eksponential-, logaritme- og trigonometriske funktioner er eksempler på funktioner, der er kontinuerte overalt, hvor de er definerede.
Kontinuitet er en vigtig forudsætning for mange af analysens sætninger, blandt andet mellemværdisætningen og sætninger om differentiabilitet.
Betydning i analysen
Kontinuitet sikrer, at små ændringer i x giver små ændringer i f(x). Denne egenskab er afgørende for at kunne definere den afledte funktion, som beskriver funktionens hældning og dermed dens lokale ændringer. Kontinuitet er derfor en grundlæggende byggesten i al analyse.