Sinus et cosinus

Si vous tracez un angle dans le cercle unité, vous pouvez lire le cosinus et le sinus sur la circonférence du cercle unité comme un point dans le système de coordonnées.

Le résultat sera toujours compris entre -1 et 1, car le point se trouve toujours sur le cercle de rayon 1.

Sur la figure, un angle de 25 degrés est tracé dans le cercle unité, et nous pouvons lire le point d’intersection sur les axes x et y.

 

 

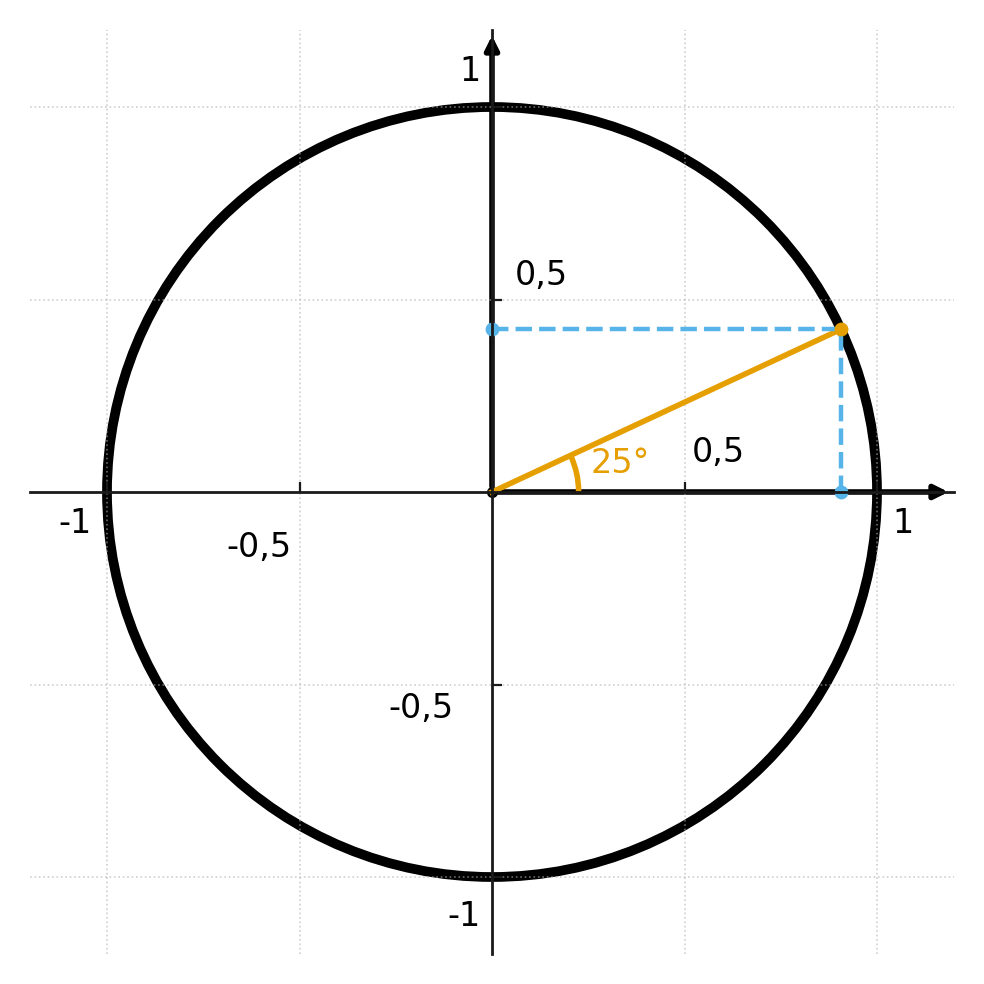
Rappelez-vous que les coordonnées se lisent toujours comme \( \large (x,y) \), ce qui correspond à \( \large (cosinus, sinus) \).

Le cosinus et le sinus sont donc le couple de coordonnées du point de référence – le point où l’angle coupe le cercle unité.

L’angle sur la figure est de 25 degrés, et si on pouvait le lire avec une précision suffisante, on verrait que :

 

$$ sin(v) \approx 0.906 $$

$$ cos(v) \approx 0.423 $$

 

Il n’est bien sûr pas possible de lire exactement sur le cercle unité, et on utilise normalement les touches cosinus et sinus sur une calculatrice.

 

Fonctions inverses

Si vous connaissez le cosinus ou le sinus d’un angle, mais pas l’angle lui-même, vous pouvez calculer dans l’autre sens avec les fonctions inverses. Celles-ci s’appellent arccos et arcsin (ou s’écrivent cos^-1 et sin^-1).

Les fonctions inverses se trouvent également sur une calculatrice, généralement sur la même touche que les fonctions ordinaires.

 

Supposons que vous sachiez que cos(A) = 0.906, mais que vous ne connaissiez pas l’angle. Vous pouvez alors le trouver ainsi :

 

$$ cos^{-1}(0.906) \approx 25^\circ $$

 

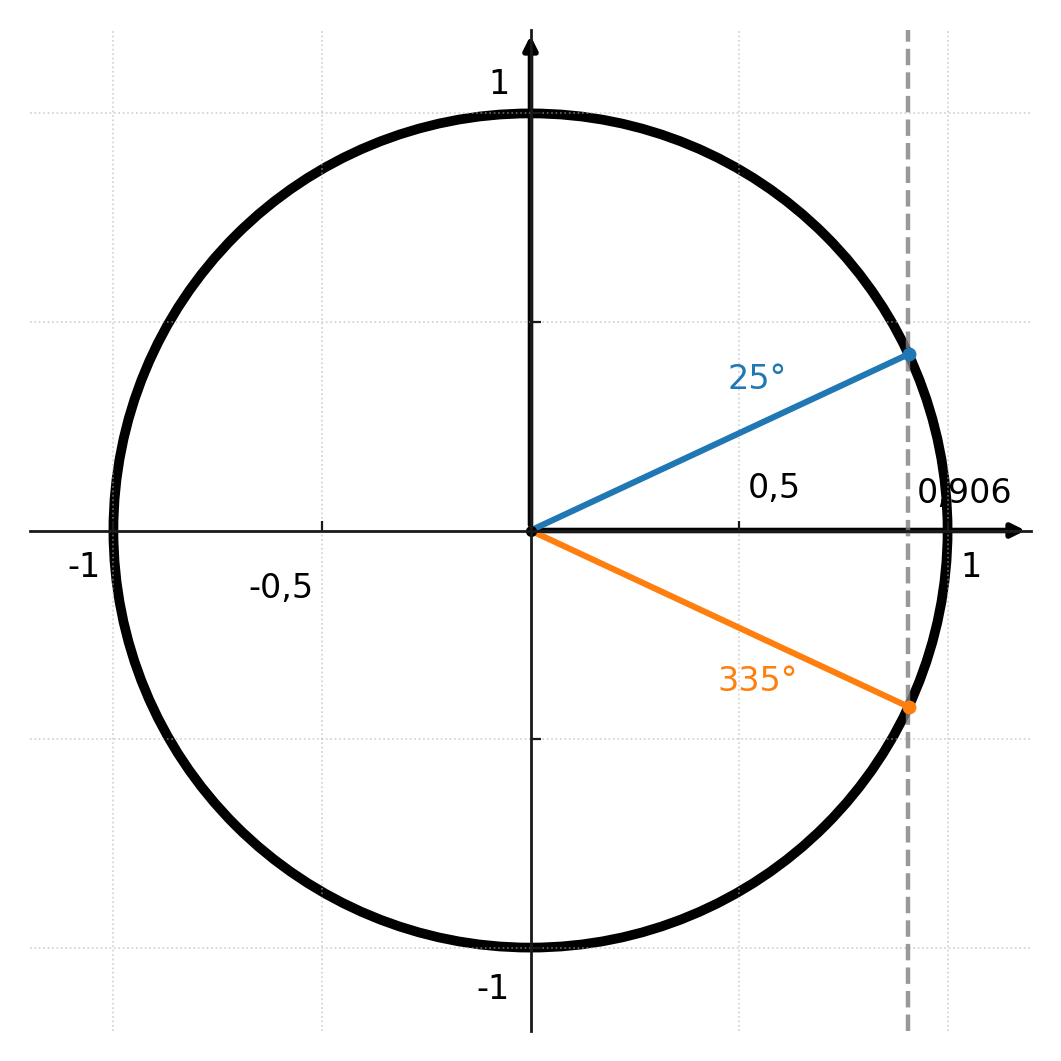
Notez que les fonctions inverses ne donnent pas toujours une solution unique. Par exemple, cos(v) = 0.906 peut correspondre à un angle de 25° et à un angle de 335° (-25°).

Pour pouvoir utiliser les fonctions comme des fonctions inverses uniques, leur définition est restreinte :

 

• Arccos est normalement limité à l’intervalle \(0^\circ \leq v \leq 180^\circ\) (\(0 \leq v \leq \pi\) rad)
• Arcsin est normalement limité à l’intervalle \(-90^\circ \leq v \leq 90^\circ\) (\(-\tfrac{\pi}{2} \leq v \leq \tfrac{\pi}{2}\) rad)

 

Cela signifie que la solution de 335° n’apparaît pas, et qu’arcsin renvoie toujours des angles dans le premier ou le quatrième quadrant.

 

 

 

 

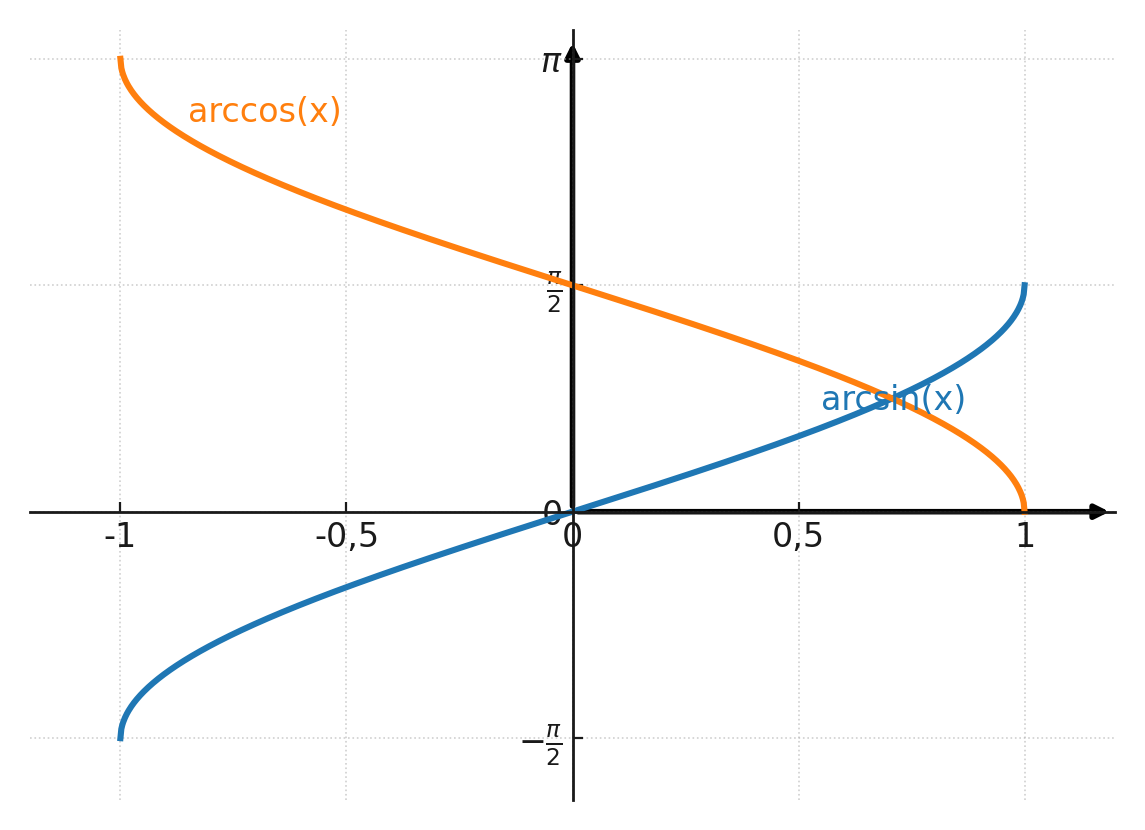
Les deux fonctions inverses sont tracées dans le système de coordonnées. Remarquez que l’axe y est en radians et non en degrés.

Si l’on lit sur la courbe arccos à x = 0.906, on obtient 0.44 rad, ce qui correspond à 25°.

 

 

 

Radians et Degrés

Pour convertir entre radians et degrés, on utilise la formule :

 

$$ \text{degrés} = \text{radians} \cdot \frac{180^\circ}{\pi} $$

$$ \text{radians} = \text{degrés} \cdot \frac{\pi}{180^\circ} $$

 

Exemple :

 

$$ 0.44 \,\text{rad} \approx 0.44 \cdot \tfrac{180^\circ}{\pi} \approx 25^\circ $$