Sécante et cosécante

Il existe également deux fonctions réciproques, à savoir la sécante et la cosécante. Elles se définissent comme les valeurs inverses du cosinus et du sinus :

 

$$ \large \sec(v) = \tfrac{1}{\cos(v)} \qquad \csc(v) = \tfrac{1}{\sin(v)} $$

 

Cela signifie que si vous connaissez le cosinus ou le sinus d’un angle, vous pouvez trouver la sécante ou la cosécante simplement en prenant la valeur réciproque.

Par exemple, si l’angle est de 25° :

 

$$ \large \cos(25^\circ) \approx 0.906 \quad \Rightarrow \quad \sec(25^\circ) \approx 1.103 $$

$$ \large \sin(25^\circ) \approx 0.423 \quad \Rightarrow \quad \csc(25^\circ) \approx 2.366 $$

 

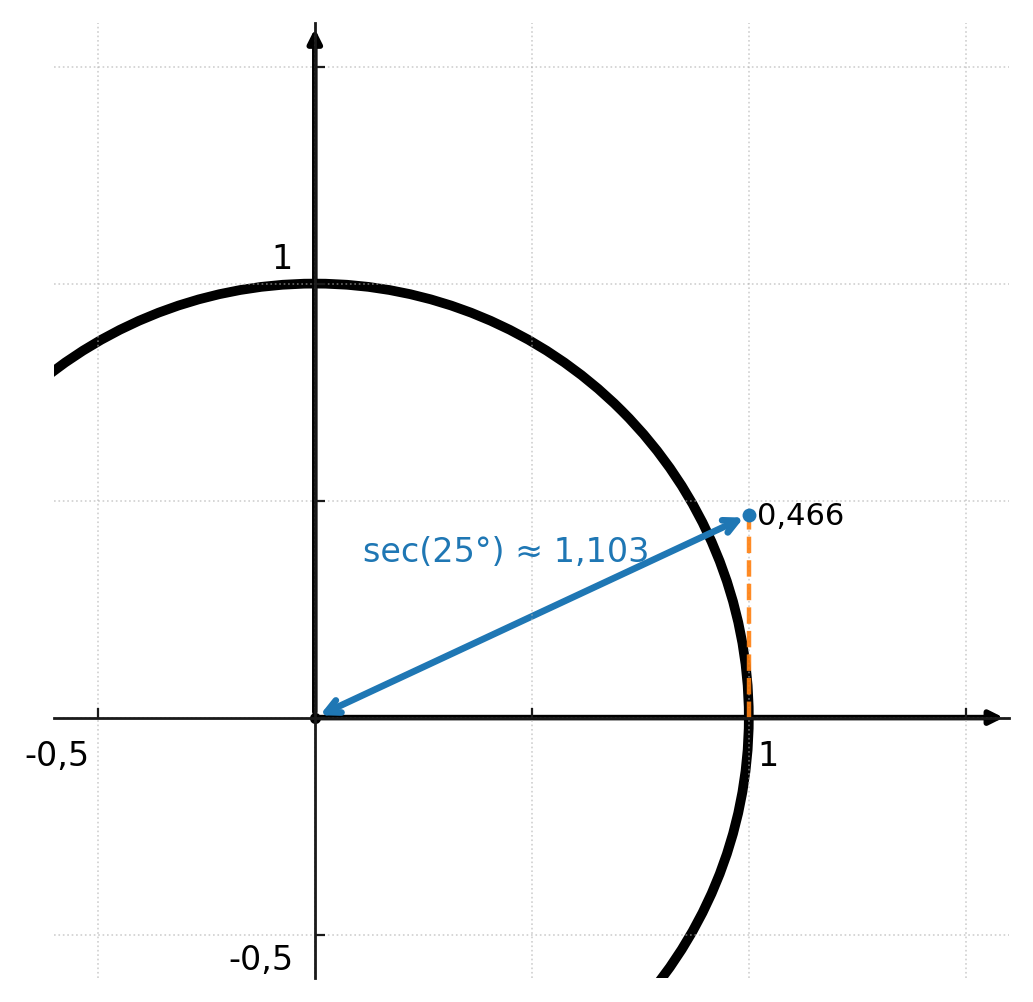
Dans le cercle unité, la sécante et la cosécante peuvent également être illustrées graphiquement.

Les deux fonctions se trouvent en prolongeant le rayon de l’angle jusqu’à ce qu’il coupe la ligne x = 1 (pour la sécante) et la ligne y = 1 (pour la cosécante).

La distance du centre au point d’intersection est la valeur de la fonction. La figure ci-dessous montre que la tangente vaut 0,466 et la sécante 1,103.

 

 

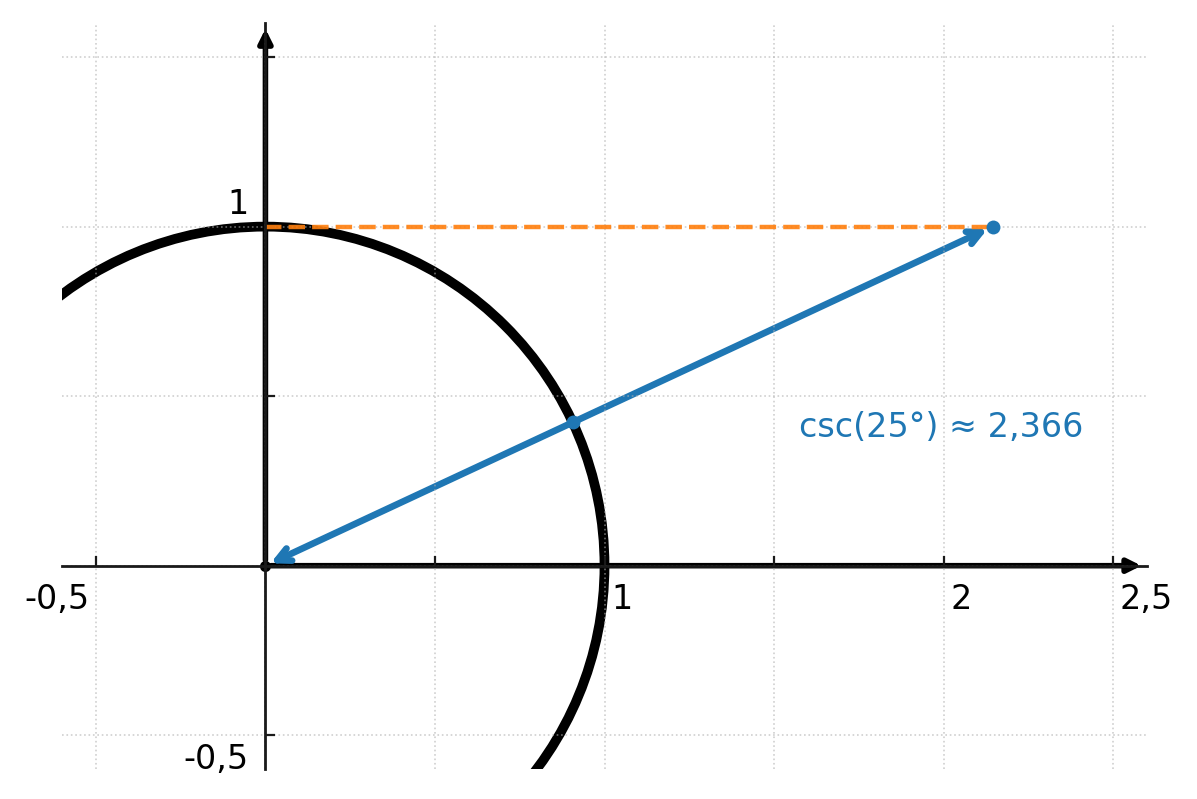
Ici, la cosécante est représentée dans le cercle unité pour un angle de 25 degrés, où la longueur du centre au point d’intersection est de 2,366

 

 

Application

La sécante et la cosécante sont surtout utiles, par exemple, en calcul différentiel et dans d’autres domaines avancés des mathématiques, où elles simplifient certains calculs.

En géométrie élémentaire, on se limite généralement au sinus, au cosinus et à la tangente.

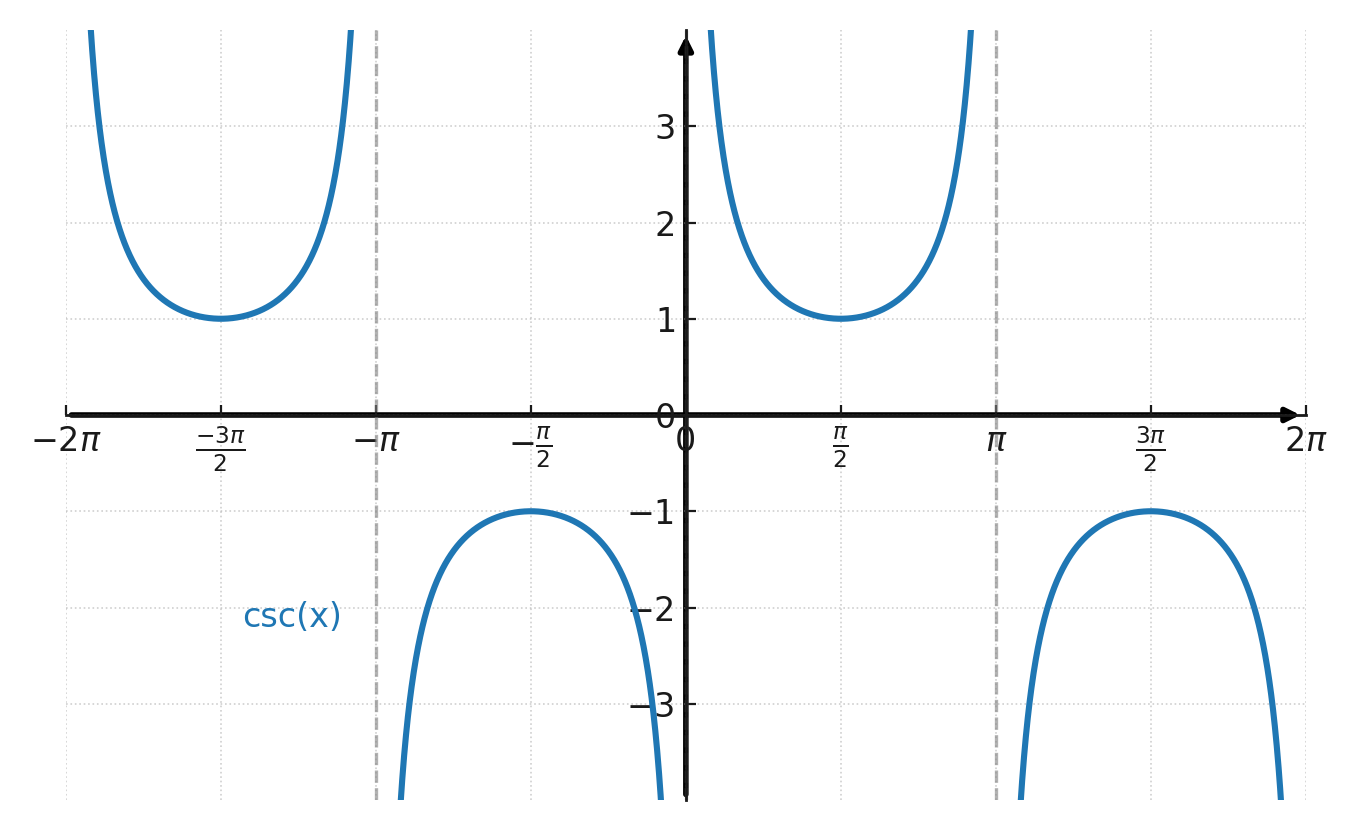
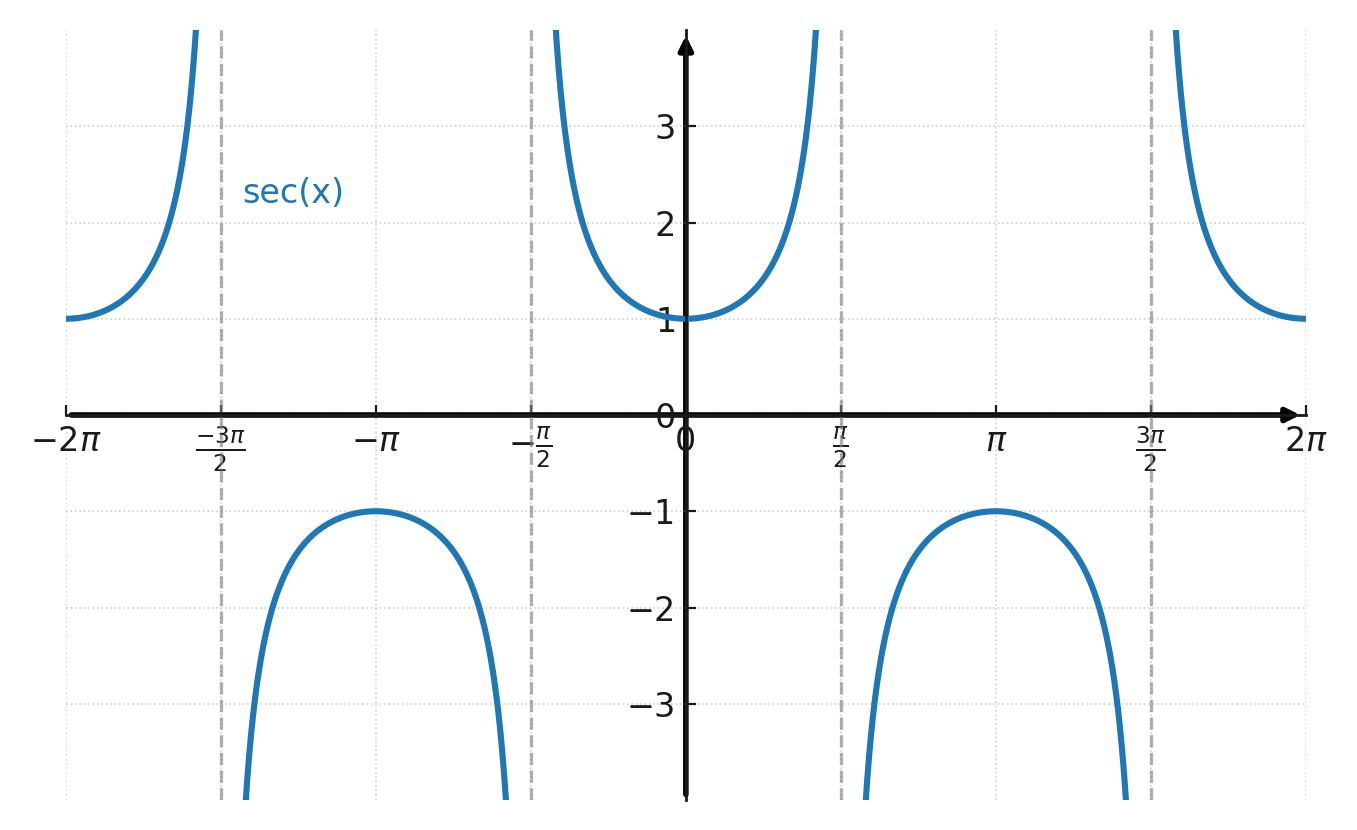
Un coup d’œil rapide aux graphiques de la sécante et de la cosécante explique pourquoi. Les fonctions ont des asymptotes verticales, prennent des valeurs très grandes et ne sont pas définies partout, contrairement au sinus et au cosinus.

 

Graphique de la sécante :

 

Graphique de la cosécante :