Trigonométrie
La trigonométrie est l’étude des relations entre les côtés et les angles d’un triangle et du calcul des grandeurs inconnues à partir de celles que l’on connaît.
La trigonométrie plane traite des relations dans un triangle plan.
En partant du cercle unité et des connaissances sur les fonctions et relations trigonométriques, il est possible de calculer presque toutes les figures géométriques, y compris celles de l’espace.

Si l’on imagine le cercle unité tracé dans un système de coordonnées, le centre du cercle est à (0,0), et il a un rayon de 1.
À partir du cercle unité, on peut définir trois fonctions, cosinus, sinus et tangente, qui servent à calculer les angles et les côtés des triangles.
La circonférence du cercle unité est \( \large 2 \cdot \pi \).
L’aire du cercle unité est \( \large \pi \).
Fonctions et relations
Il existe au total six fonctions trigonométriques. Dans un triangle rectangle, elles se définissent ainsi :
| Fonction | Définition |
|---|---|
| Sinus (sin) | \( \Large \sin(v) = \tfrac{\text{côté opposé}}{\text{hypoténuse}} \) |
| Cosinus (cos) | \( \Large \cos(v) = \tfrac{\text{côté adjacent}}{\text{hypoténuse}} \) |
| Tangente (tan) | \( \Large \tan(v) = \tfrac{\text{côté opposé}}{\text{côté adjacent}} \) |
| Cotangente (cot) | \( \Large \cot(v) = \tfrac{\text{côté adjacent}}{\text{côté opposé}} \) |
| Sécante (sec) | \( \Large \sec(v) = \tfrac{\text{hypoténuse}}{\text{côté adjacent}} \) |
| Coscécante (csc) | \( \Large \csc(v) = \tfrac{\text{hypoténuse}}{\text{côté opposé}} \) |
Pour la géométrie ordinaire, les trois premières sont les plus importantes à connaître. Il est aussi important de savoir utiliser les relations du sinus et du cosinus.
Ligne, point et angle de référence
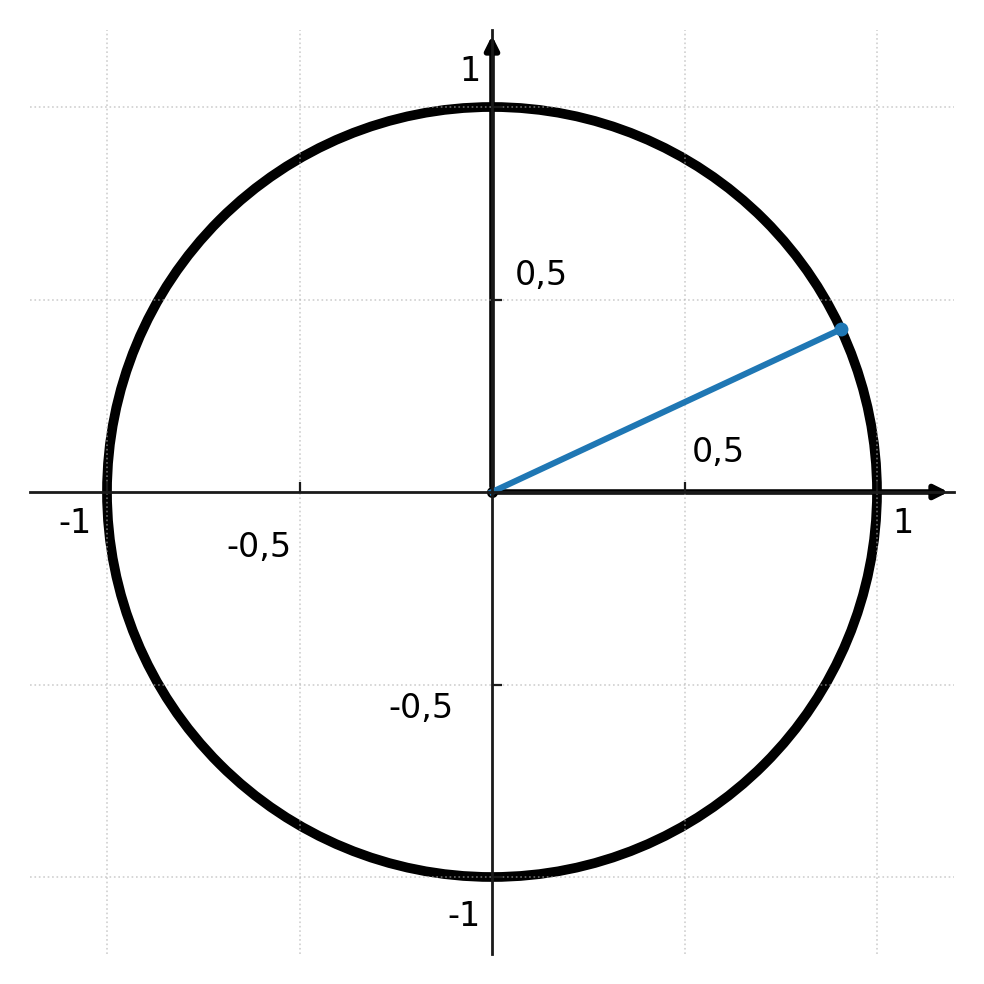
Si vous tracez une ligne du centre (0,0) jusqu’à un point aléatoire sur l’arc du cercle, la ligne formera un angle avec l’axe des x du système de coordonnées.
Le point que vous avez choisi sur l’arc du cercle s’appelle le point de référence. La ligne que vous avez tracée s’appelle la ligne de référence, et l’angle formé avec l’axe des x s’appelle l’angle de référence.
Si vous connaissez l’angle d’un triangle, vous pouvez le dessiner dans le cercle, et le point de référence sera la base de votre calcul du triangle.
Trigonométrie sphérique
La trigonométrie sphérique traite des triangles et d’autres figures géométriques à la surface d’une sphère.
Tout comme nous avons le cercle unité de rayon 1 en trigonométrie plane, on peut imaginer une sphère unité de rayon 1.
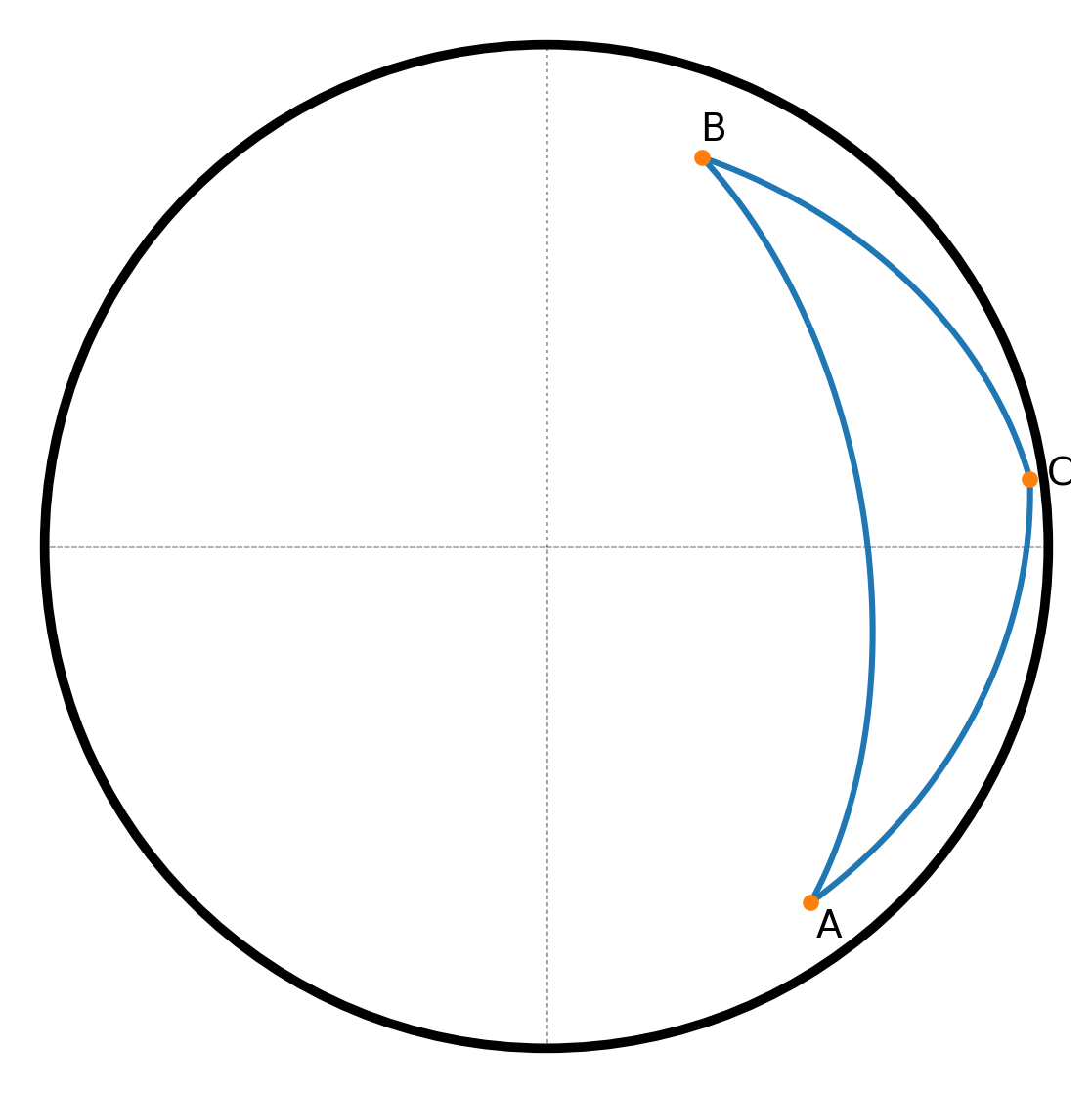
Un triangle sphérique est formé par trois arcs de grands cercles à la surface de la sphère. À l’aide des fonctions trigonométriques, on peut calculer les dépendances réciproques entre côtés et angles de tels triangles.
La trigonométrie sphérique a été développée en particulier pour la navigation et l’astronomie.