Loi des sinus
La loi des sinus peut être utilisée dans les cas où l’on connaît une paire angle-côté, c’est-à-dire lorsque l’un des côtés connus se trouve en face de l’angle connu.
Ainsi, si vous connaissez l’angle \(A\) et les côtés \(a\) et \(b\), vous devez utiliser la loi des sinus.
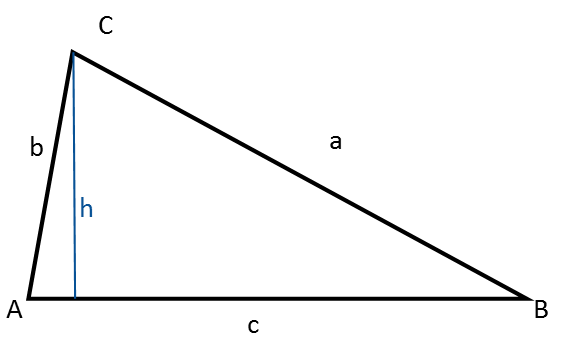
Un triangle arbitraire n’est ni rectangle, ni équilatéral, ni isocèle.
La loi des sinus s’écrit ainsi :
$$ {a \over \sin(A)} = {b \over \sin(B)} = {c \over \sin(C)} $$
Ainsi, si vous connaissez l’angle \(A\) et les côtés \(a\) et \(b\), et que vous devez trouver l’angle \(B\), vous utilisez ce qui suit et isolez l’angle \(B\) :
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] \sin(B) = {b \cdot \sin(A) \over a} $$
Le résultat sera un nombre compris entre 0 et 1, par exemple 0,866. Pour trouver l’angle, vous devez utiliser \( \sin^{-1} \) sur votre calculatrice :
$$ \sin^{-1}(0,866) = 60^\circ $$
L’angle est donc de 60 degrés.
Si vous connaissez deux angles et seulement un côté, vous pouvez également utiliser la loi des sinus. Supposons que vous connaissiez les angles \(A\) et \(B\), ainsi que le côté \(a\) :
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] b = {a \cdot \sin(B) \over \sin(A)} $$
Remarque : si le calcul donne \(\sin(v) > 1\), il n’existe pas de solution. Cela signifie que le triangle donné ne peut pas exister avec les informations que vous avez.
Sinus et triangles obtus
Si vous calculez des angles avec le sinus dans un triangle qui se révèle obtus, vous devez faire attention, car il peut y avoir deux résultats selon ce que vous savez du triangle.
Supposons que vous ayez les informations suivantes sur un triangle :
- Angle A = 25 degrés
- Côté a = 3
- Côté c = 5
Avec ces informations, nous pouvons calculer l’angle \(C\) :
$$ \begin{align}{a \over \sin(A)} &= {c \over \sin(C)} \Leftrightarrow \\[10pt] \sin(C) &= {c \cdot \sin(A) \over a } \Leftrightarrow \\[10pt] \sin(C) &= {5 \cdot \sin(25^\circ) \over 3 } \Leftrightarrow \\[10pt] \sin(C) &= 0,704 \Leftrightarrow \\[10pt] \sin^{-1}(0,704) &= 44,78^\circ \end{align} $$
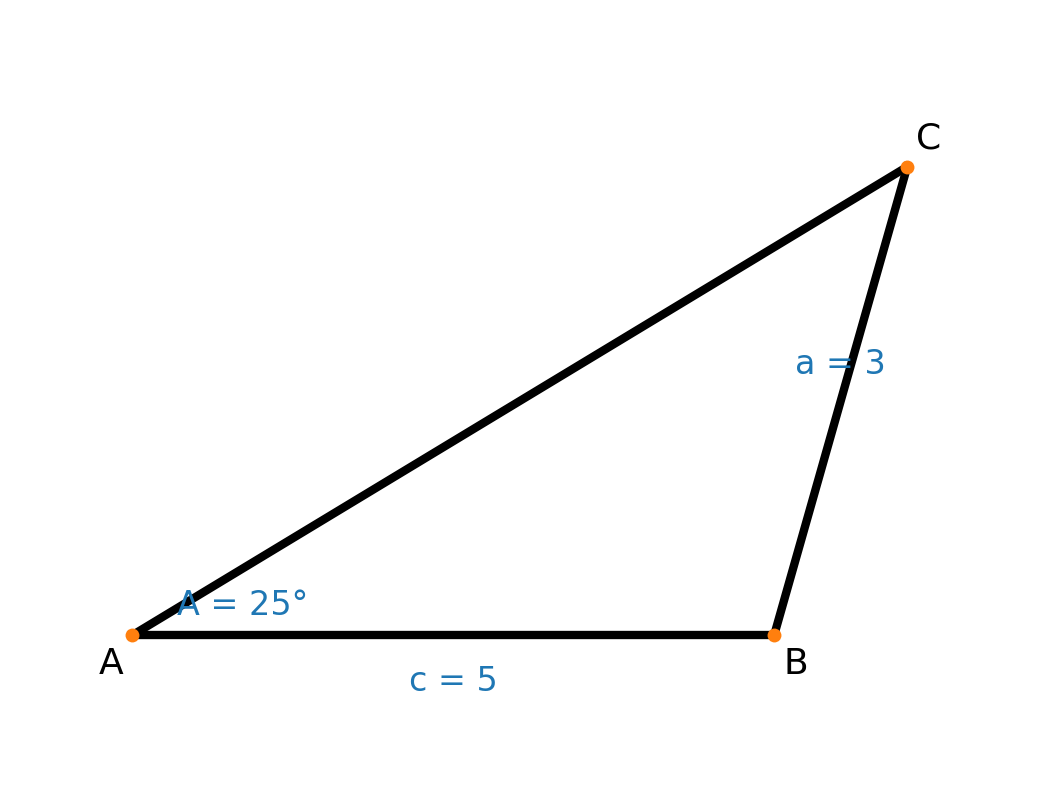
Le résultat est donc un triangle, comme indiqué ci-dessus, avec :
- Angle A = 25°
- Angle B = 110,22°
- Angle C = 44,78°
Calcul de l’angle obtus
Si vous regardez la figure ci-dessous, vous pouvez voir qu’il est possible de tracer un autre triangle avec les mêmes informations.
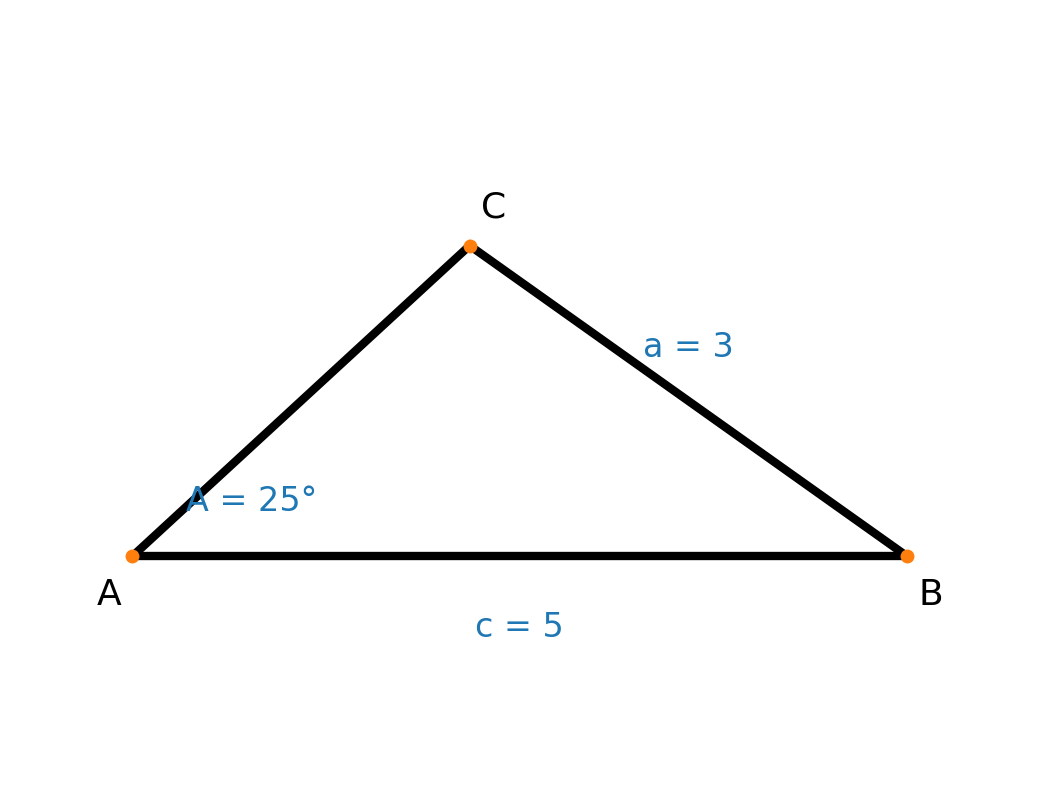
La loi des sinus donne toujours la solution aiguë (entre 0° et 90°). La solution obtuse possible se trouve en soustrayant l’angle aigu de 180°.
Nous supposons que l’angle aigu est de 44,78°, comme calculé précédemment, et l’appelons \(C_1\). L’angle obtus, nous l’appelons \(C_2\) :
$$ C_2 = 180 - C_1 \Leftrightarrow \\[12pt] C_2 = 135,22^\circ $$
Vous connaissez donc l’angle \(C\) pour les deux triangles et pouvez calculer le reste pour les deux. Cela signifie que le côté \(b\) a également deux longueurs différentes (il en va de même pour le périmètre, la hauteur et l’aire).
Il faut donc toujours vérifier si la solution trouvée peut avoir un angle obtus lorsque vous utilisez la loi des sinus.
La règle pour savoir quand il y a deux solutions est : Si l’angle que vous calculez avec la loi des sinus est inférieur à 90 degrés, il y aura deux résultats.