Loi des cosinus

La loi des cosinus peut être utilisée dans les triangles quelconques, c’est-à-dire les triangles qui ne sont ni rectangles, ni isocèles, ni équilatéraux. Elle fonctionne aussi bien lorsque vous connaissez deux côtés et l’angle compris que lorsque vous connaissez les trois côtés.

 

Formules de la loi des cosinus

Si vous connaissez un angle et les deux côtés qui forment cet angle, vous pouvez trouver le troisième côté à l’aide de la loi des cosinus :

 

$$ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(A) $$

$$ b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(B) $$

$$ c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(C) $$

 

Remarque : si le triangle est rectangle, il suffit d’utiliser le théorème de Pythagore. La loi des cosinus est particulièrement utile pour les triangles quelconques.

 

Calcul des angles

Si vous connaissez les trois côtés d’un triangle, vous pouvez trouver les angles en isolant le cosinus dans la formule :

 

$$ \cos(A) = \frac{b^2 + c^2 - a^2}{2 \cdot b \cdot c} $$

$$ \cos(B) = \frac{a^2 + c^2 - b^2}{2 \cdot a \cdot c} $$

$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2 \cdot a \cdot b} $$

 

Le résultat sera un nombre compris entre -1 et 1. Pour trouver l’angle, utilisez \( \cos^{-1} \) sur votre calculatrice :

 

$$ \cos^{-1}(0,866) = 30^\circ $$

 

L’angle est donc de 30 degrés.

 

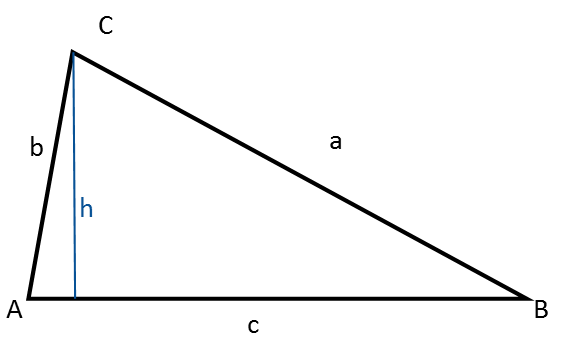
Un triangle quelconque n’est ni rectangle, ni équilatéral, ni isocèle.

Remarquez que la hauteur le divise en deux triangles rectangles.