Équations différentielles

Une équation différentielle décrit la relation entre une fonction et sa dérivée. Au lieu d’indiquer directement quelle est la fonction, elle décrit comment elle change. Cela fait des équations différentielles un outil essentiel en mathématiques, physique, biologie et économie, où de nombreux phénomènes concernent précisément des changements au cours du temps.

 

 

Qu’est-ce qu’une équation différentielle

Une équation ordinaire contient une grandeur inconnue, par exemple \( \large x \). En revanche, une équation différentielle contient une fonction inconnue \( \large y(x) \) et ses dérivées, comme \( \large y'(x) \) ou \( \large y''(x) \). Le but est de trouver la fonction \( \large y(x) \) qui satisfait l’équation.

 

Exemples :

 

$$ \large y' = 3x^2 $$

 

$$ \large y'' + y = 0 $$

 

La première équation indique que la pente de \( \large y \) est toujours \( \large 3x^2 \). La seconde décrit une oscillation, car elle relie la fonction à sa propre dérivée seconde.

 

 

Idée de base

Une équation différentielle ne dit pas directement à quoi ressemble la courbe de \( \large y \), mais comment sa pente varie d’un point à l’autre. On peut donc la considérer comme une recette pour un mouvement ou une croissance.

 

Si la dérivée est connue, on peut retrouver la fonction en effectuant l’opération inverse de la dérivation — c’est-à-dire en intégrant. Ainsi, les équations différentielles sont étroitement liées au calcul intégral.

 

 

Ordre et types

Une équation différentielle ordinaire (abrégée ODE) ne comporte qu’une seule variable indépendante, généralement \( \large x \) ou \( \large t \). Si l’équation comporte plusieurs variables et des dérivées par rapport à plusieurs d’entre elles, on parle alors d’une équation différentielle partielle (PDE).

 

L’ordre d’une équation différentielle est la dérivée de plus haut ordre qui y figure. Par exemple :

 

• \( \large y' = 3x^2 \) → équation du premier ordre
• \( \large y'' + y = 0 \) → équation du second ordre

 

 

Résolution d’équations différentielles simples

Les équations différentielles les plus simples peuvent être résolues directement par intégration. Par exemple, si

 

$$ \large y' = 3x^2 $$

 

alors \( \large y(x) \) peut être trouvée en intégrant le côté droit :

 

$$ \large y = \int 3x^2 \, dx = x^3 + C $$

 

Ici, \( \large C \) est la constante d’intégration, représentant toutes les solutions possibles — c’est-à-dire toutes les courbes ayant le même motif de pente mais des positions verticales différentes.

 

 

Séparation des variables

Une méthode courante pour résoudre les équations du premier ordre est la séparation des variables. Si l’équation peut s’écrire comme

 

$$ \large \frac{dy}{dx} = g(x) \cdot h(y) $$

 

alors \( \large x \) et \( \large y \) peuvent être séparées et intégrées de chaque côté :

 

$$ \large \int \frac{1}{h(y)} \, dy = \int g(x) \, dx $$

 

Exemple : Résoudre \( \large y' = 2xy \).

 

Séparer les variables : \( \large \frac{1}{y} dy = 2x dx \).

 

Intégrer les deux côtés :

 

$$ \large \ln|y| = x^2 + C $$

 

Réécrire la solution générale :

 

$$ \large y = A e^{x^2} $$

 

où \( \large A = e^C \) est une constante. Cette méthode fonctionne chaque fois que les variables peuvent être séparées de cette manière.

 

 

Équations différentielles linéaires du premier ordre

Une équation linéaire du premier ordre a la forme :

 

$$ \large y' + p(x)y = q(x) $$

 

La solution se trouve en multipliant toute l’équation par un facteur intégrant :

 

$$ \large \mu(x) = e^{\int p(x)\,dx} $$

 

On peut alors écrire l’équation sous la forme

 

$$ \large (\mu(x)y)' = \mu(x)q(x) $$

 

et l’intégrer directement. Cette approche est appelée la méthode du facteur intégrant.

 

 

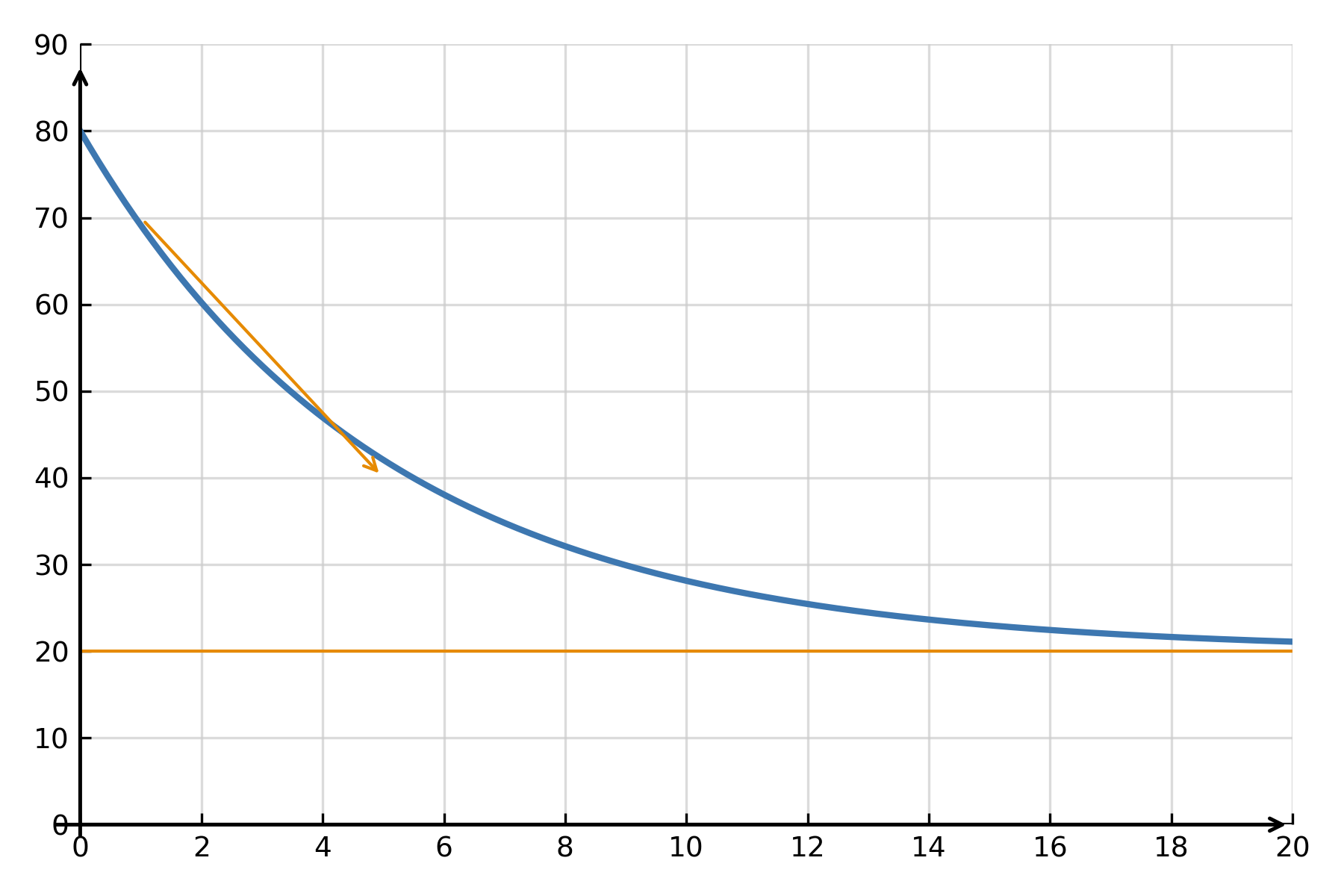
Exemple : Loi du refroidissement de Newton

Un exemple classique d’équation différentielle linéaire est la loi du refroidissement de Newton :

 

$$ \large \frac{dT}{dt} = -k(T - T_{\text{env}}) $$

 

Ici, \( \large T(t) \) représente la température d’un objet qui se refroidit vers la température ambiante \( \large T_{\text{env}} \), et \( \large k \) est une constante. La solution montre que la température se rapproche de celle du milieu de façon exponentielle :

 

$$ \large T(t) = T_{\text{env}} + (T_0 - T_{\text{env}})e^{-kt} $$

 

Ce type d’équation apparaît également dans la désintégration radioactive, la décharge de condensateurs et les modèles économiques d’ajustement.

 

 

 

Équations différentielles du second ordre

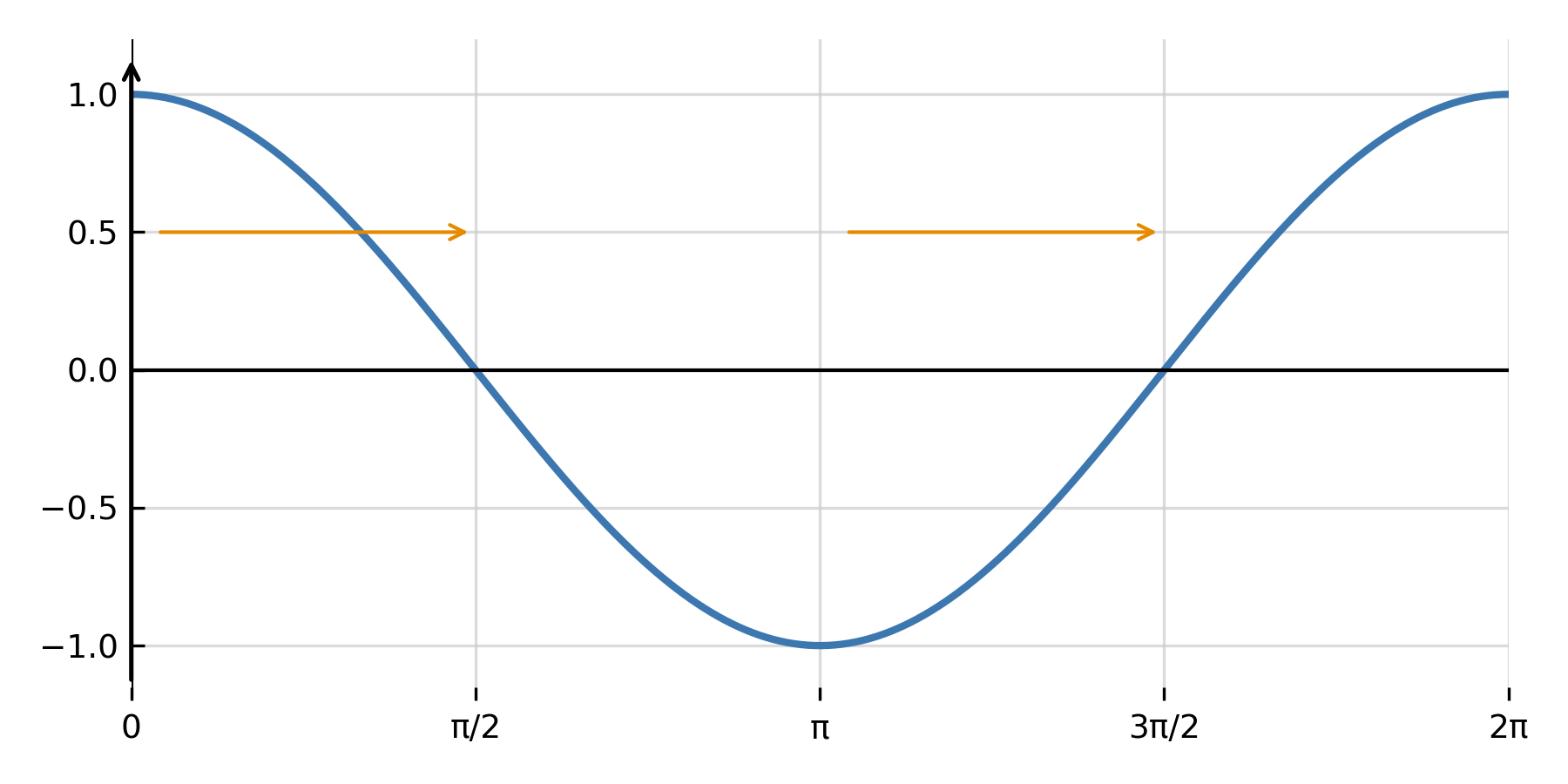
Lorsque la dérivée seconde intervient, l’équation décrit souvent un mouvement ou une oscillation. Un exemple important est l’oscillation harmonique :

 

$$ \large y'' + \omega^2 y = 0 $$

 

La solution est une combinaison de sinus et de cosinus :

 

$$ \large y = A \cos(\omega x) + B \sin(\omega x) $$

 

Ici, \( \large A \) et \( \large B \) représentent les conditions initiales, tandis que \( \large \omega \) indique la fréquence d’oscillation. Ce type d’équation est utilisé en mécanique, en théorie des ondes et dans les circuits électriques.

 

 

 

Solutions numériques

Dans de nombreux cas, une équation différentielle ne peut pas être résolue analytiquement. On utilise alors des méthodes numériques, où la fonction est calculée point par point à partir de sa dérivée. Les méthodes les plus connues sont la méthode d’Euler, de Runge–Kutta et la méthode de la sécante, toutes expliquées dans la section Méthodes numériques.

 

 

Résumé

Les équations différentielles décrivent comment les fonctions changent et jouent un rôle central dans les mathématiques appliquées. Elles servent à modéliser la croissance, le mouvement, les oscillations, la chaleur, le courant et bien d’autres phénomènes. Certaines peuvent être résolues à la main, d’autres nécessitent des méthodes numériques, mais toutes relient le calcul différentiel et le calcul intégral dans un système unifié.