Tangente et cotangente

La tangente est également une fonction trigonométrique qui nous renseigne sur l’angle dans le cercle unité. Contrairement au cosinus et au sinus, le résultat peut être supérieur à 1.

La définition de la tangente est :

 

$$ tan(v) = \frac{sin(v)}{cos(v)} $$

 

Cela signifie qu’un angle (A) de 25 degrés se calcule ainsi :

 

$$ tan(v) = \frac{sin(v)}{cos(v)} \qquad \Leftrightarrow $$

$$ tan(v) = \frac{sin(25^\circ)}{cos(25^\circ)} \qquad \Leftrightarrow $$

$$ tan(v) = \frac{0.423}{0.906} \qquad \Leftrightarrow $$

$$ tan(v) \approx 0.467 $$

 

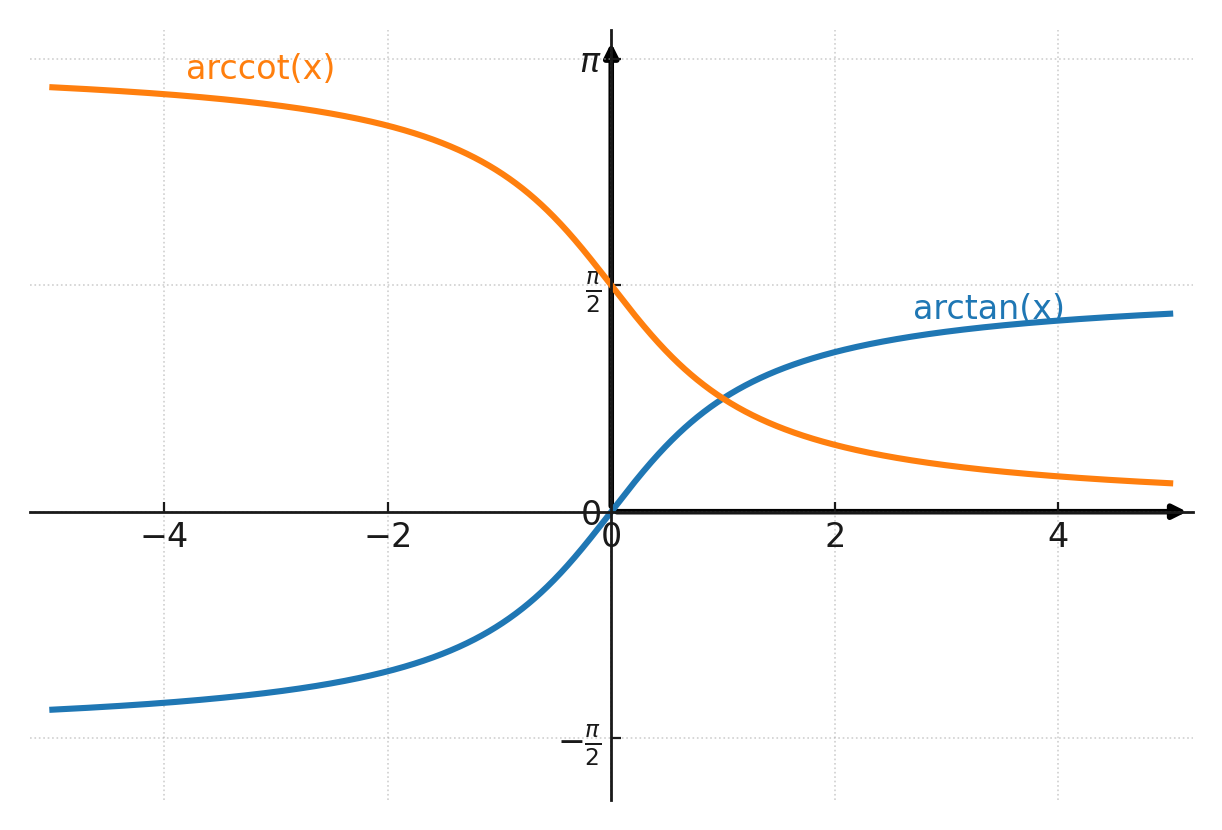
La tangente peut également se lire dans le cercle unité. On commence par tracer une ligne verticale tangente au cercle unité au point \((1, 0)\).

On peut alors voir où l’angle coupe la ligne. La coordonnée y du point d’intersection est la tangente de l’angle.

 

 

Cotangente

La cotangente est le réciproque de la tangente :

 

$$ cot(v) = \frac{cos(v)}{sin(v)} $$

 

La cotangente est moins utilisée, car le sinus, le cosinus et la tangente suffisent pour effectuer les calculs géométriques les plus courants.

On ne trouve généralement pas non plus de touche cot sur les calculatrices ordinaires.

 

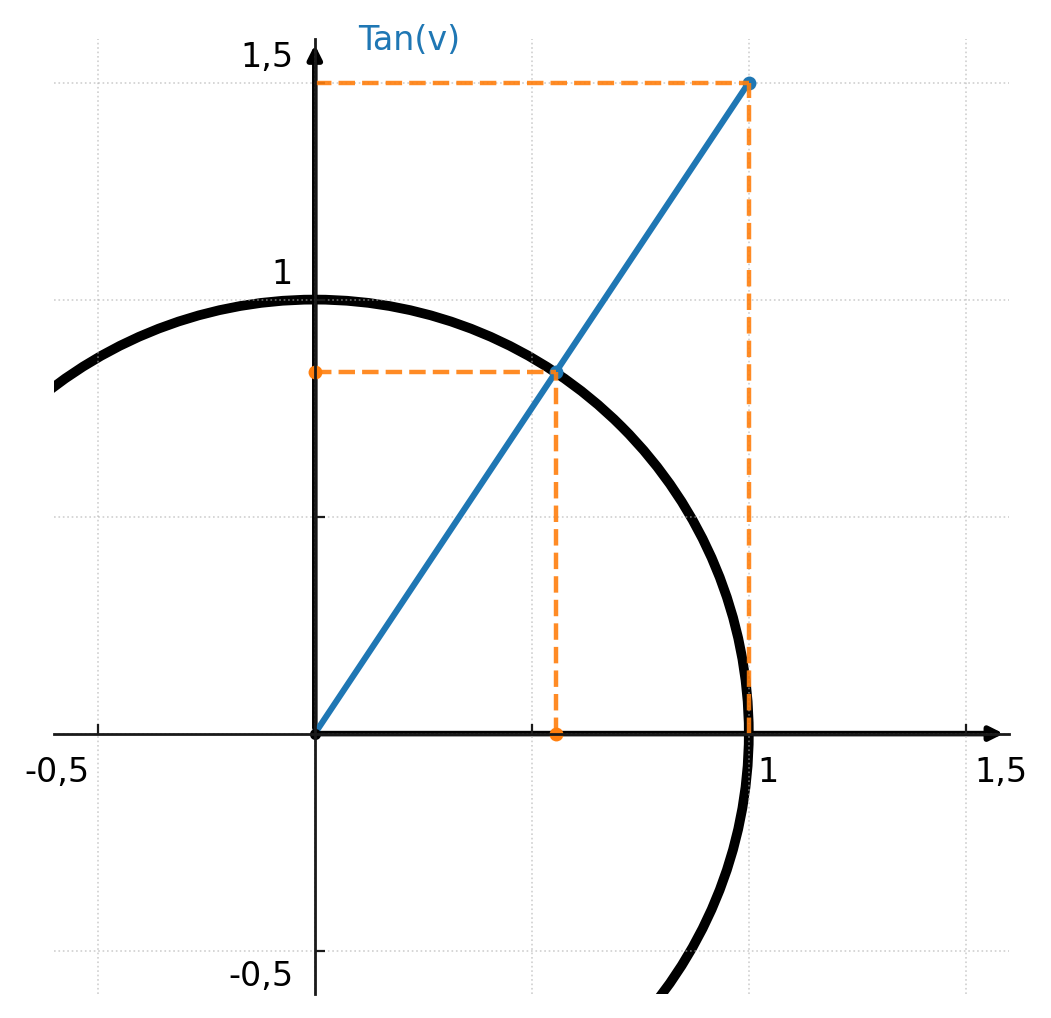
Dans le cercle unité, la cotangente part horizontalement du point \((0,1)\) et se lit sur l’axe des x là où elle coupe l’angle :

 

 

L’angle de 25 degrés se calcule ainsi :

 

$$ cot(v) = \frac{cos(v)}{sin(v)} \qquad \Leftrightarrow $$

$$ cot(v) = \frac{cos(25^\circ)}{sin(25^\circ)} \qquad \Leftrightarrow $$

$$ cot(v) = \frac{0.906}{0.423} \qquad \Leftrightarrow $$

$$ cot(v) \approx 2.14 $$

 

Fonctions inverses

Tout comme arcsin et arccos, il existe également des fonctions inverses pour la tangente et la cotangente. Celles-ci s’appellent arctan et arccot (ou s’écrivent tan^-1 et cot^-1).

Si vous connaissez la tangente d’un angle, mais pas l’angle lui-même, vous pouvez le trouver avec arctan. Par exemple, nous savons que :

 

$$ tan(45^\circ) = 1 $$

 

Il en découle également que :

 

$$ tan^{-1}(1) = 45^\circ $$

 

Arctan peut être utilisé pour calculer un angle à partir du rapport entre deux côtés d’un triangle rectangle.

 

Arccot fonctionne de la même manière pour la cotangente. Si vous connaissez la cotangente d’un angle, vous pouvez trouver l’angle avec arccot. Par exemple :

 

$$ cot(45^\circ) = 1 \qquad \Leftrightarrow \qquad cot^{-1}(1) = 45^\circ $$

 

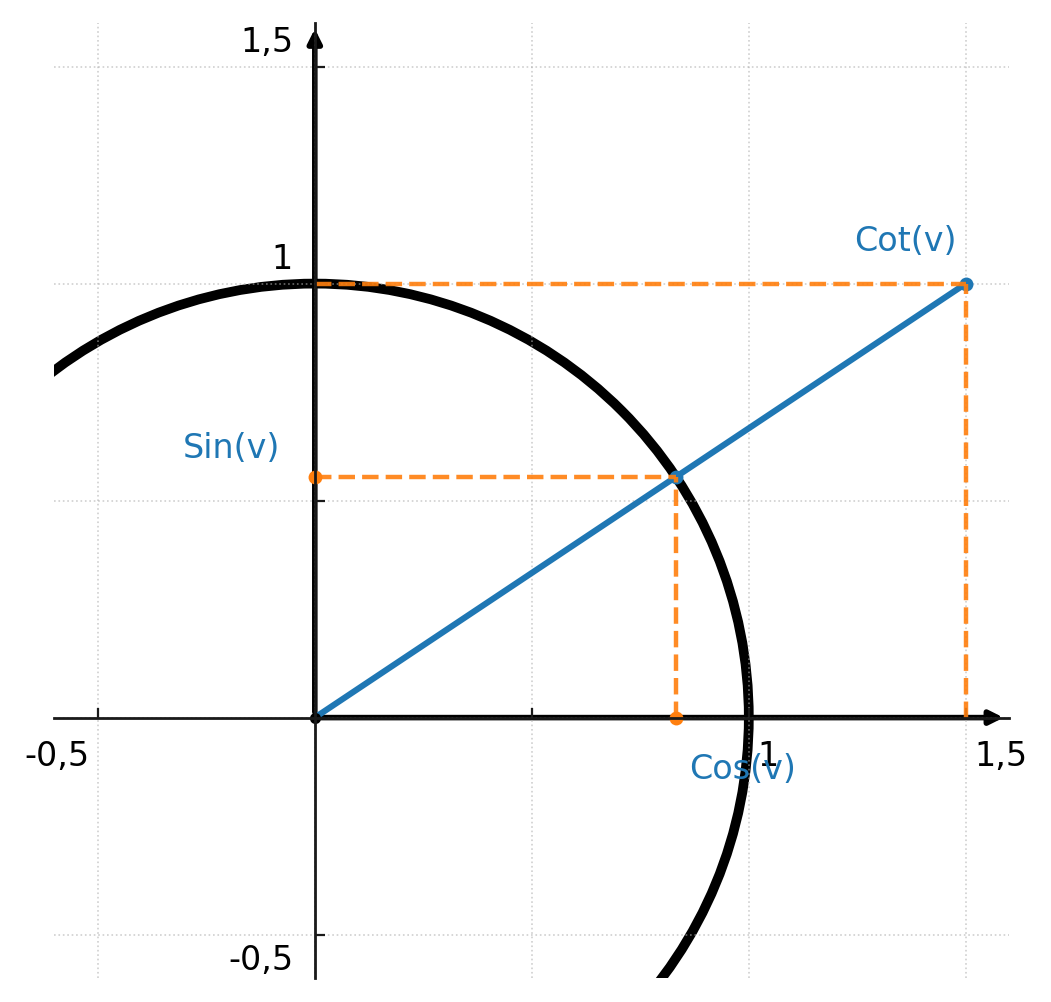
Les deux fonctions donneraient deux solutions si elles n’étaient pas restreintes. Ici, on voit les deux solutions de arctan dans le premier et le troisième quadrant :

 

 

Les fonctions sont restreintes de la manière suivante :

 

• Pour arctan, l’angle est limité à l’intervalle \(-90^\circ \leq v \leq 90^\circ\)
• Pour arccot, l’angle est limité à l’intervalle \(0^\circ \leq v \leq 180^\circ\)

 

De cette façon, les fonctions sont uniques !

 

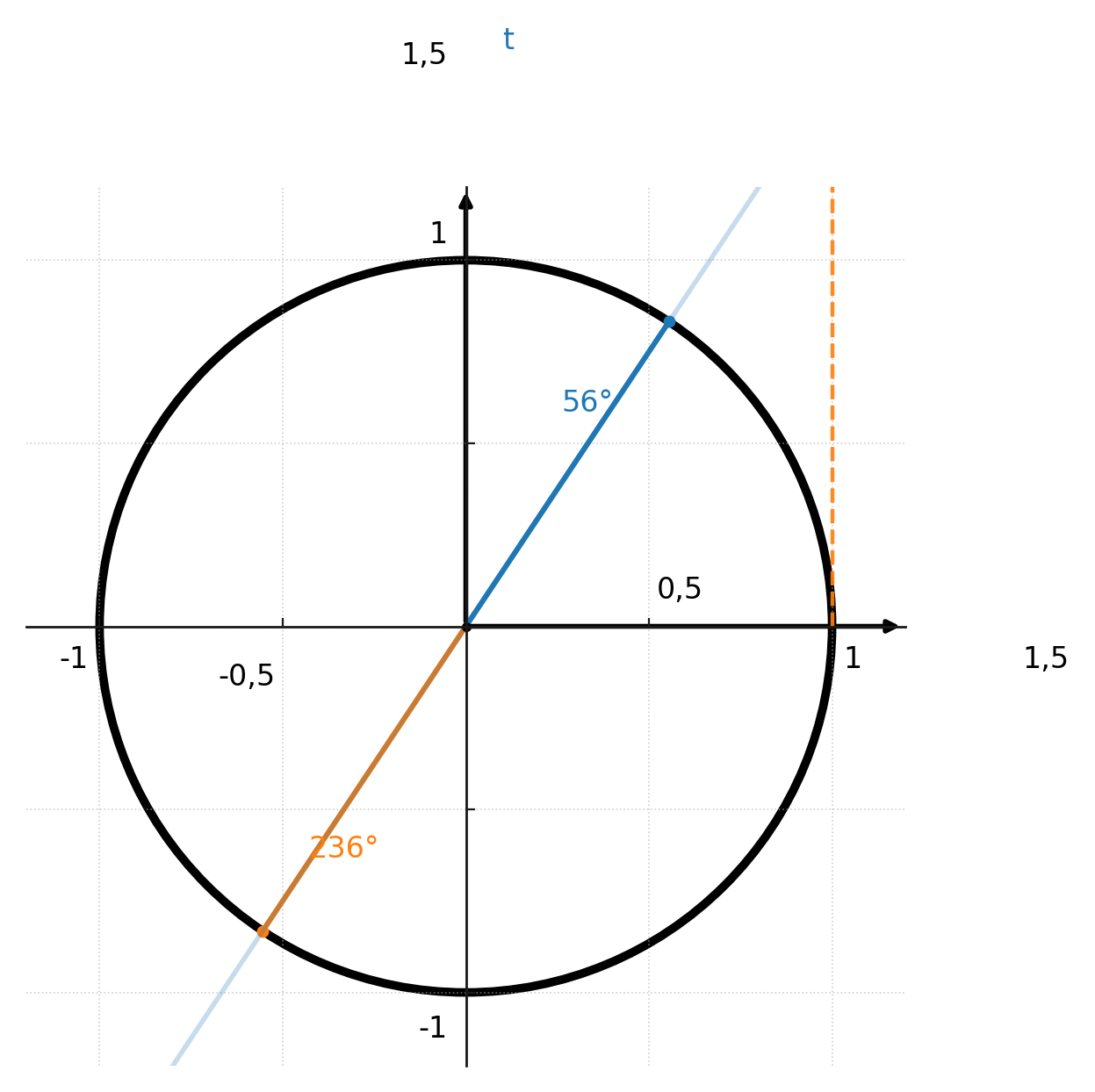
Les deux fonctions inverses sont tracées dans le système de coordonnées. Remarquez que l’axe y est en radians et non en degrés.