Relations

En trigonométrie, les relations sont les formules et les connexions qui relient entre elles les fonctions trigonométriques. Alors que les fonctions (sinus, cosinus, tangente, etc.) décrivent chacune un rapport spécifique, les relations montrent comment les fonctions sont liées et peuvent être utilisées pour calculer les côtés et les angles dans les triangles.

 

Identité de Pythagore

L’une des relations les plus fondamentales est l’identité de Pythagore, qui montre la connexion entre sinus et cosinus pour tout angle :

 

$$ \sin^2(v) + \cos^2(v) = 1 $$

 

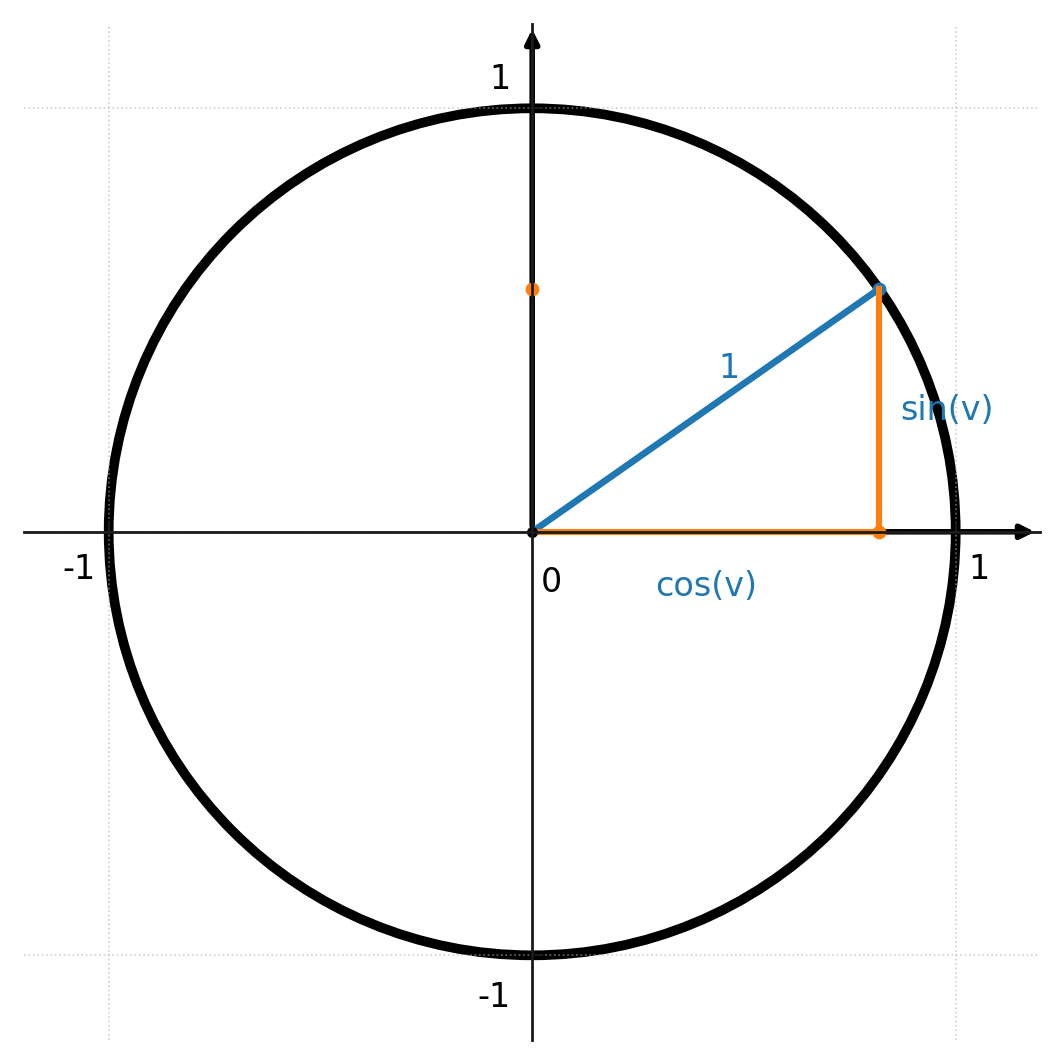
L’identité découle directement du cercle unité.

Si un point du cercle a pour coordonnées \( (\cos v, \sin v) \), le théorème de Pythagore s’applique, car le rayon est toujours égal à 1 :

 

$$ (\cos v)^2 + (\sin v)^2 = 1^2 = 1 $$

 

 

Application

L’identité de Pythagore permet de calculer le sinus si l’on connaît le cosinus, ou le cosinus si l’on connaît le sinus.

C’est aussi la base de nombreuses autres identités trigonométriques.

 

Exemple : Si \( \cos v = 0.6 \), on peut trouver le sinus ainsi :

 

$$ \sin^2(v) = 1 - \cos^2(v) = 1 - 0.6^2 = 0.64 $$

$$ \sin(v) = \pm \sqrt{0.64} = \pm 0.8 $$

 

Remarquez qu’il y a deux solutions, car l’angle peut se trouver dans le premier comme dans le deuxième quadrant.

 

L’identité de Pythagore est la relation trigonométrique la plus fondamentale et constitue la base de nombreuses autres formules et calculs en trigonométrie.