Funciones inversas
Una función es biyectiva si es tanto inyectiva como sobreyectiva.
Esto significa que cada elemento en el dominio \( \large A\) corresponde a exactamente un elemento en el codominio \( \large B\), y que todo \( \large B\) queda cubierto.
Así, existe una correspondencia única que puede invertirse.
Definición
Una función \( \large f : A \to B\) es biyectiva si:
$$ \large \forall a_1,a_2 \in A: f(a_1)=f(a_2) \Rightarrow a_1=a_2 \quad (\text{inyectividad}) $$
$$ \large \forall b \in B \;\exists a \in A : f(a)=b \quad (\text{sobreyectividad}) $$
La combinación de estas dos propiedades asegura que la función puede “invertirse”.
Existencia de la función inversa
Si \( \large f : A \to B\) es biyectiva, existe una función inversa \( \large f^{-1} : B \to A\), que cumple:
$$ \large f^{-1}(f(a)) = a \quad \text{para todo } a \in A $$
$$ \large f(f^{-1}(b)) = b \quad \text{para todo } b \in B $$
La inversa “anula” el efecto de la función original.
Ejemplos
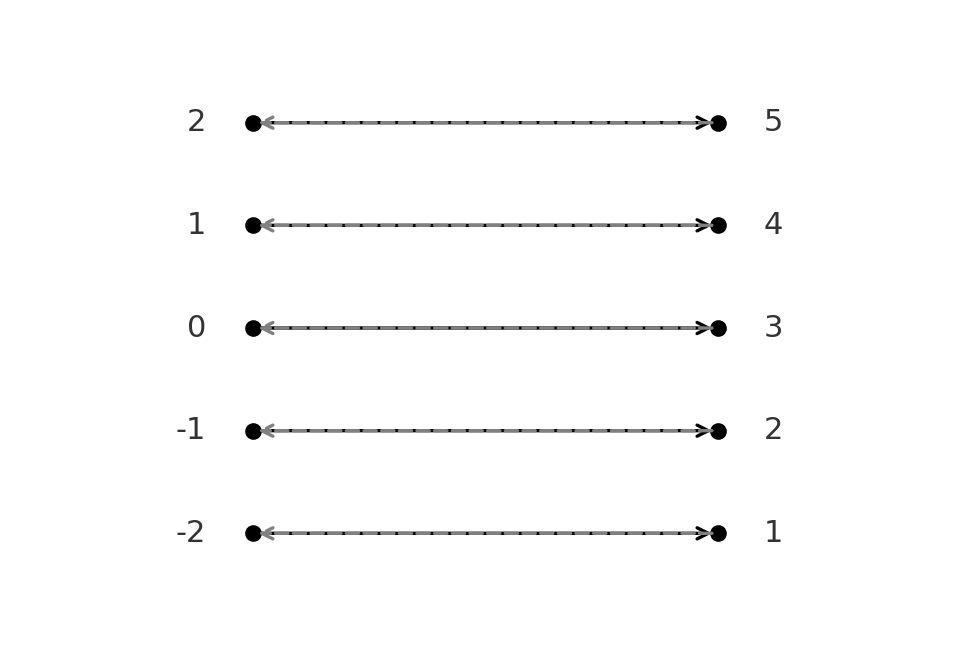
Función biyectiva: \( \large f(x)=x+3\) de \( \large \mathbb{Z} \to \mathbb{Z}\) es biyectiva.
La función inversa es \( \large f^{-1}(y)=y-3\).
Función no biyectiva: \( \large f(x)=x^2\) de \( \large \mathbb{R} \to \mathbb{R}\) no es biyectiva, porque no es inyectiva (tanto \( \large -2\) como \( \large 2\) dan la imagen \( \large 4\)).
Por lo tanto, aquí no existe función inversa.
Aplicación
Las funciones biyectivas y sus inversas juegan un papel central en muchas áreas de las matemáticas y la informática:
- Criptografía: Los algoritmos de cifrado requieren funciones que puedan invertirse de manera única para que los mensajes puedan descifrarse.
- Álgebra: Los isomorfismos entre estructuras algebraicas son biyecciones que preservan la estructura.
- Lógica y teoría: En las demostraciones matemáticas, las biyecciones se usan para comparar el tamaño de los conjuntos (cardinalidad).
Comprender las funciones biyectivas es por tanto crucial tanto para aplicaciones teóricas como prácticas.