Funciones inyectivas, suprayectivas y biyectivas
En matemáticas, las funciones pueden tener diferentes propiedades según cómo se relacionen los elementos del dominio y del codominio.
Las tres más importantes son inyectiva, sobreyectiva y biyectiva.
Función inyectiva
Una función \( \large f : A \to B\) es inyectiva si dos elementos diferentes en \( \large A\) siempre tienen imágenes diferentes en \( \large B\).
En otras palabras:
$$ \large f(a_1) = f(a_2) \;\Rightarrow\; a_1 = a_2 $$
Ejemplo:
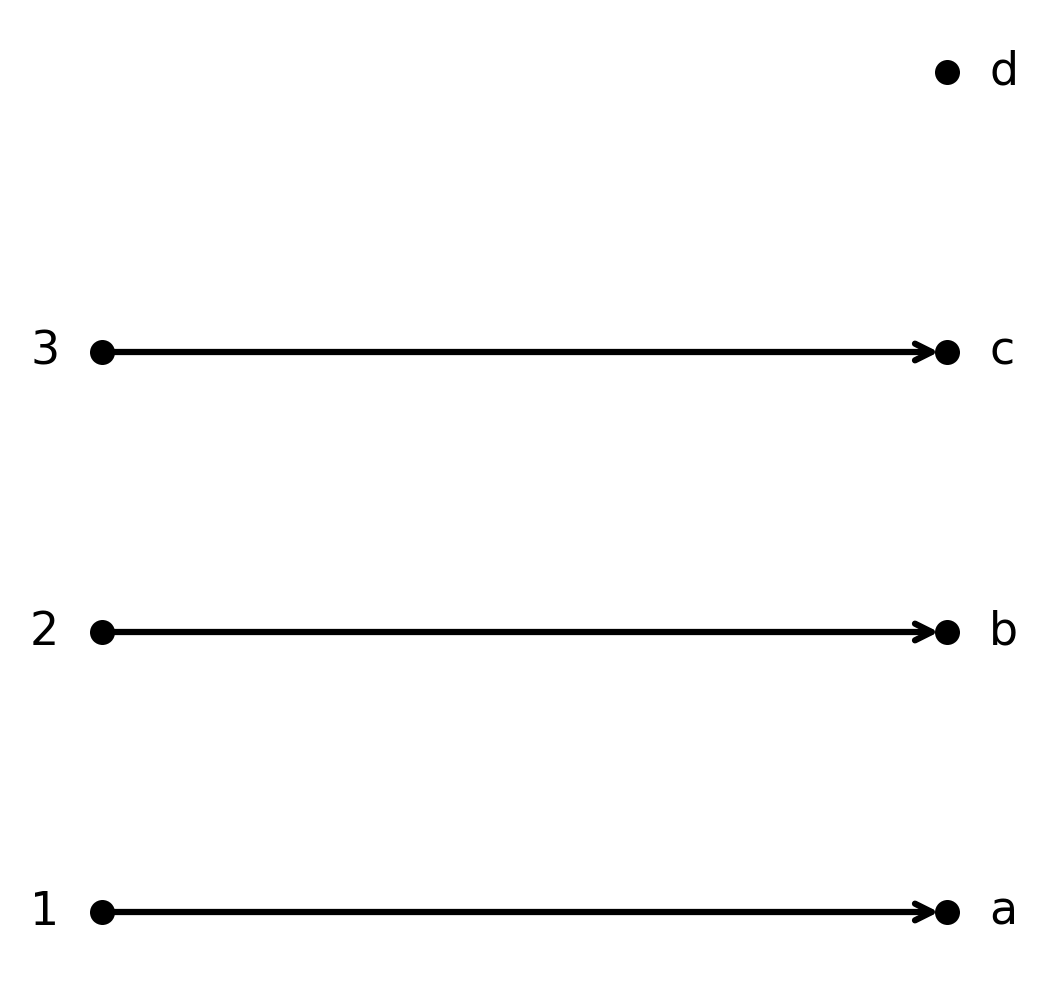
La función \( \large f : \{1,2,3\} \to \{a,b,c,d\}\) dada por \( \large f(1)=a, f(2)=b, f(3)=c\) es inyectiva.
Cada elemento de \( \large A\) se asocia con un elemento único de \( \large B\), pero no se cubre todo el codominio.
Función sobreyectiva
Una función \( \large f : A \to B\) es sobreyectiva si cada elemento en \( \large B\) es alcanzado por al menos un elemento de \( \large A\).
Es decir:
$$ \large \forall b \in B, \;\exists a \in A : f(a) = b $$
Ejemplo:
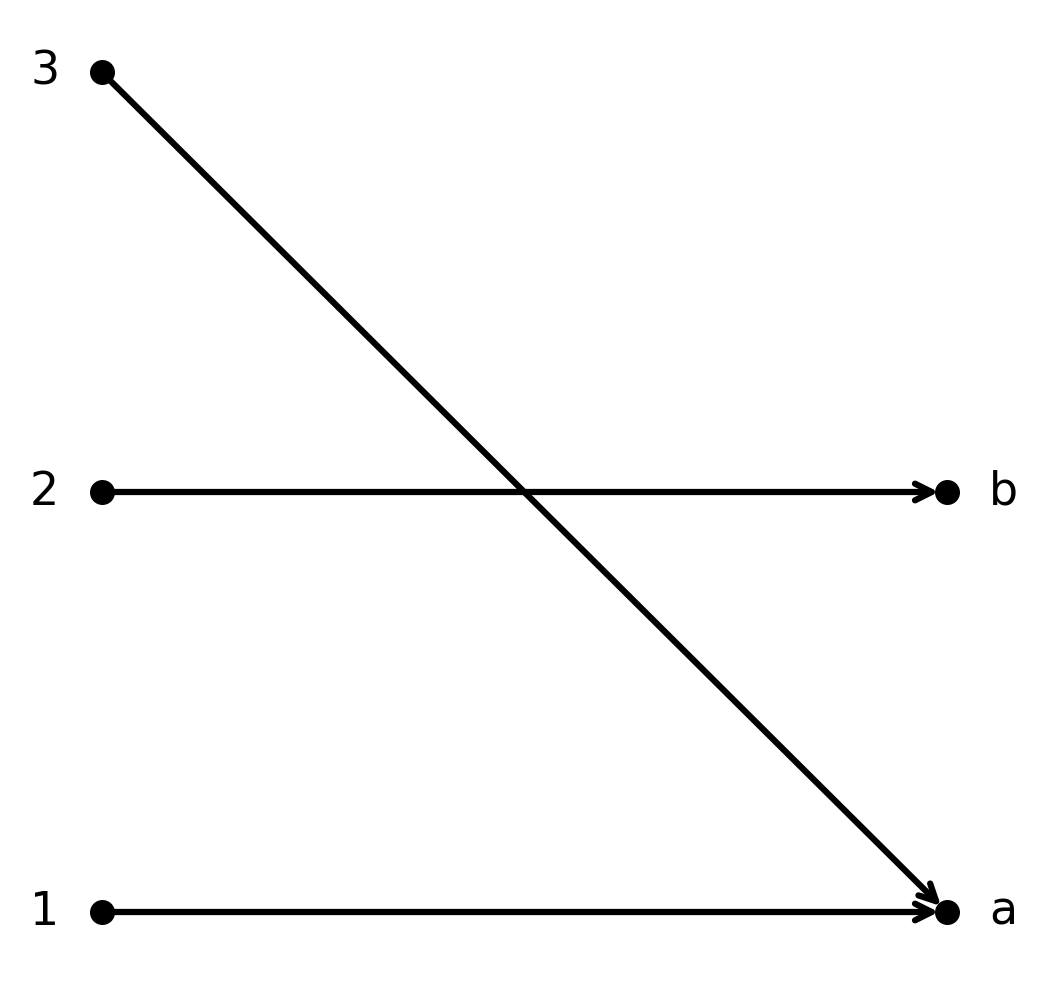
La función \( \large f : \{1,2,3\} \to \{a,b\}\) dada por \( \large f(1)=a, f(2)=b, f(3)=a\) es sobreyectiva.
Ambos elementos de \( \large B\) son alcanzados, pero la función no es inyectiva porque \( \large 1\) y \( \large 3\) se asocian con \( \large a\).
Función biyectiva
Una función es biyectiva si es tanto inyectiva como sobreyectiva.
Esto significa que existe una correspondencia uno a uno entre los elementos de \( \large A\) y \( \large B\). Cada elemento de \( \large A\) se asocia con un elemento único de \( \large B\), y todo \( \large B\) queda cubierto.
Ejemplo:
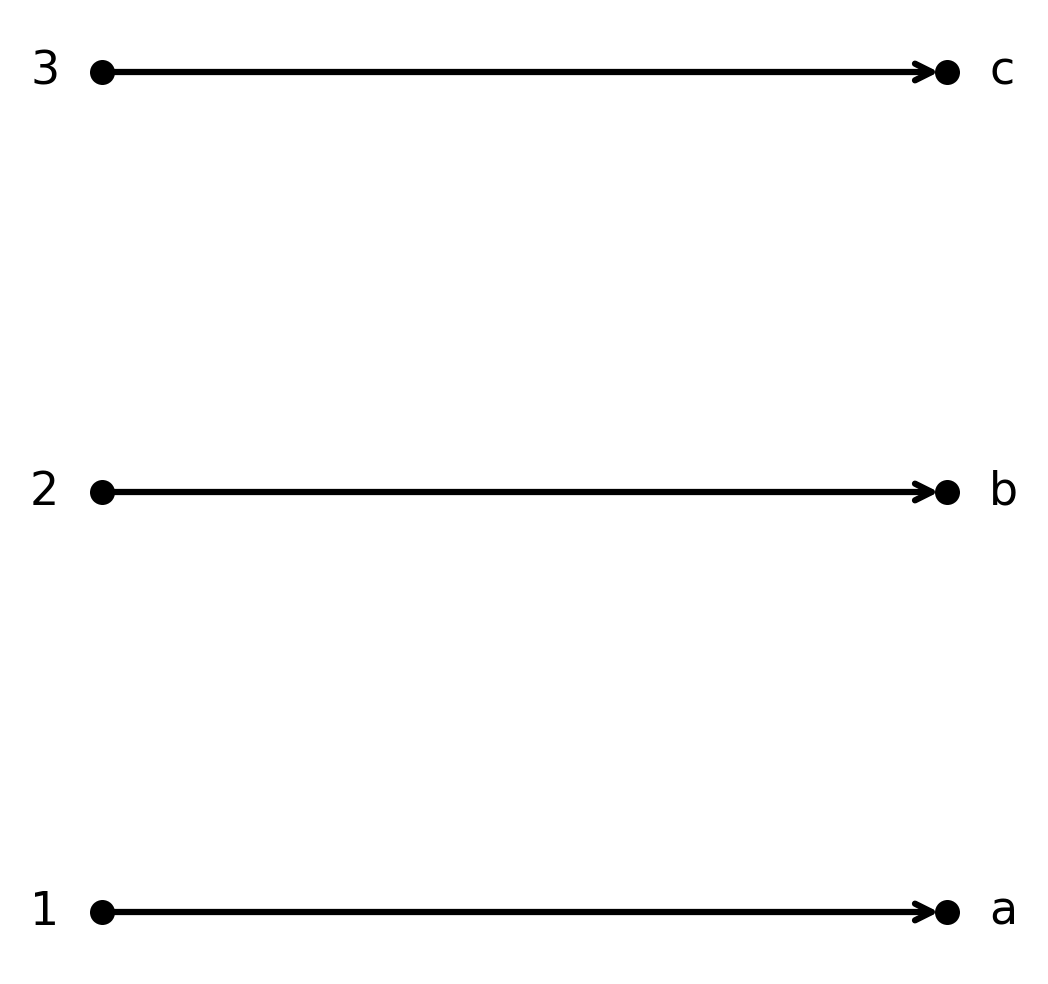
La función \( \large f : \{1,2,3\} \to \{a,b,c\}\) dada por \( \large f(1)=a, f(2)=b, f(3)=c\) es biyectiva.
Cada elemento de \( \large A\) se asocia con un elemento único de \( \large B\), y todos los elementos de \( \large B\) son alcanzados.
Resumen
- Inyectiva: Dos entradas diferentes siempre producen salidas diferentes.
- Sobreyectiva: Todo el codominio está cubierto.
- Biyectiva: Combinación de ambas – existe una correspondencia uno a uno que puede invertirse.
Las funciones biyectivas son especialmente importantes porque siempre tienen una función inversa, lo que permite volver del resultado a la entrada.