Ejemplos de funciones

Para comprender mejor las propiedades de las funciones, vemos aquí ejemplos concretos en los conjuntos numéricos clásicos: los números naturales \( \large \mathbb{N}\), los enteros \( \large \mathbb{Z}\) y los números reales \( \large \mathbb{R}\).

 

Ejemplo 1: Función inyectiva en \( \large \mathbb{N}\)

La función \( \large f : \mathbb{N} \to \mathbb{N}\) dada por \( \large f(n) = 2n\).

 

$$ \large f(n) = 2n $$

 

 

 

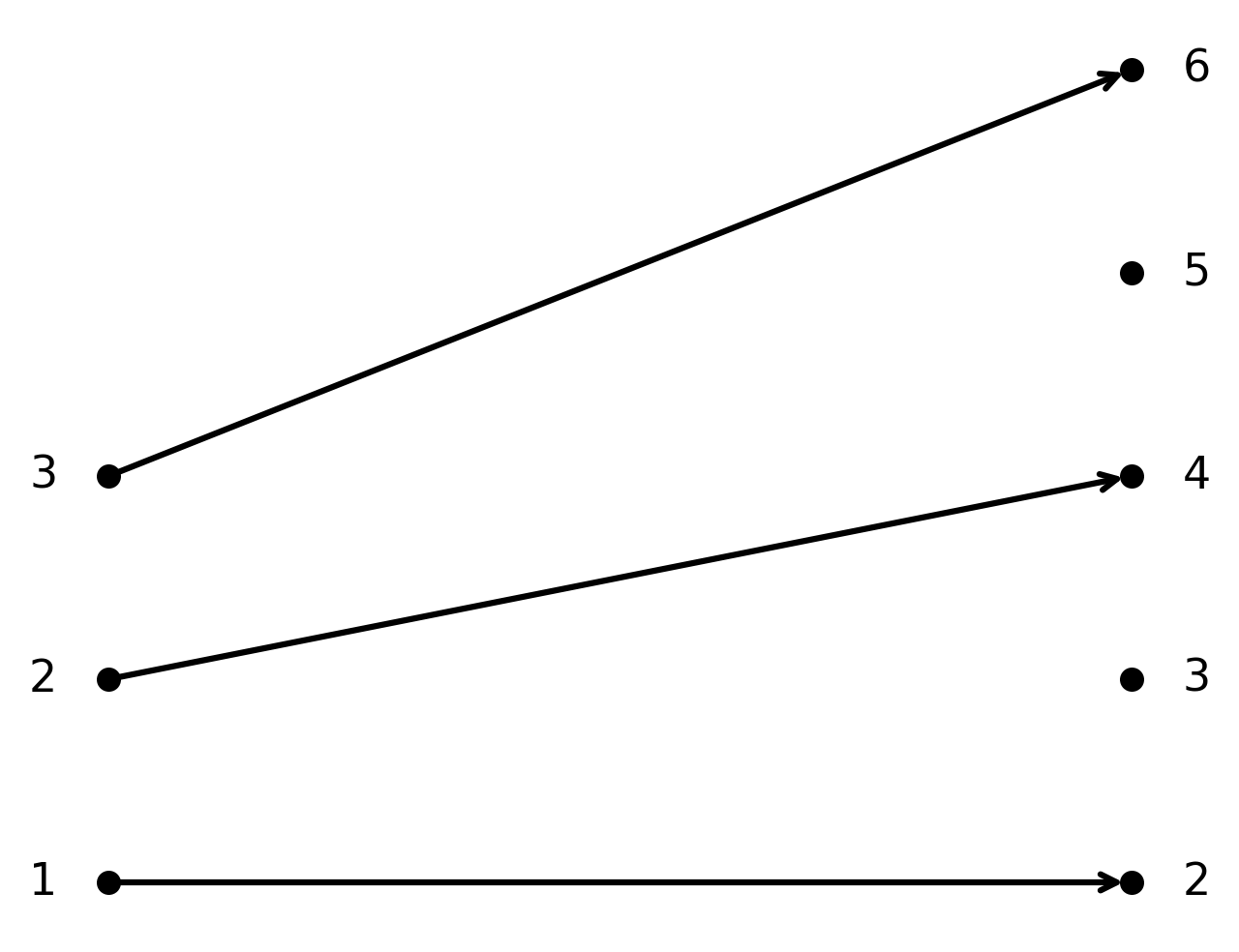
Aquí \( f\) es inyectiva, porque dos números naturales diferentes siempre dan resultados diferentes al multiplicarse por 2. Pero la función no es sobreyectiva, ya que los números impares no son alcanzados.

 

 

Ejemplo 2: Función sobreyectiva en \( \large \mathbb{Z}\)

La función \( \large f : \mathbb{Z} \to \mathbb{Z}\) dada por \( \large f(n) = \lfloor \frac{n}{2} \rfloor\).

 

$$ \large f(n) = \left\lfloor \frac{n}{2} \right\rfloor $$

 

 

 

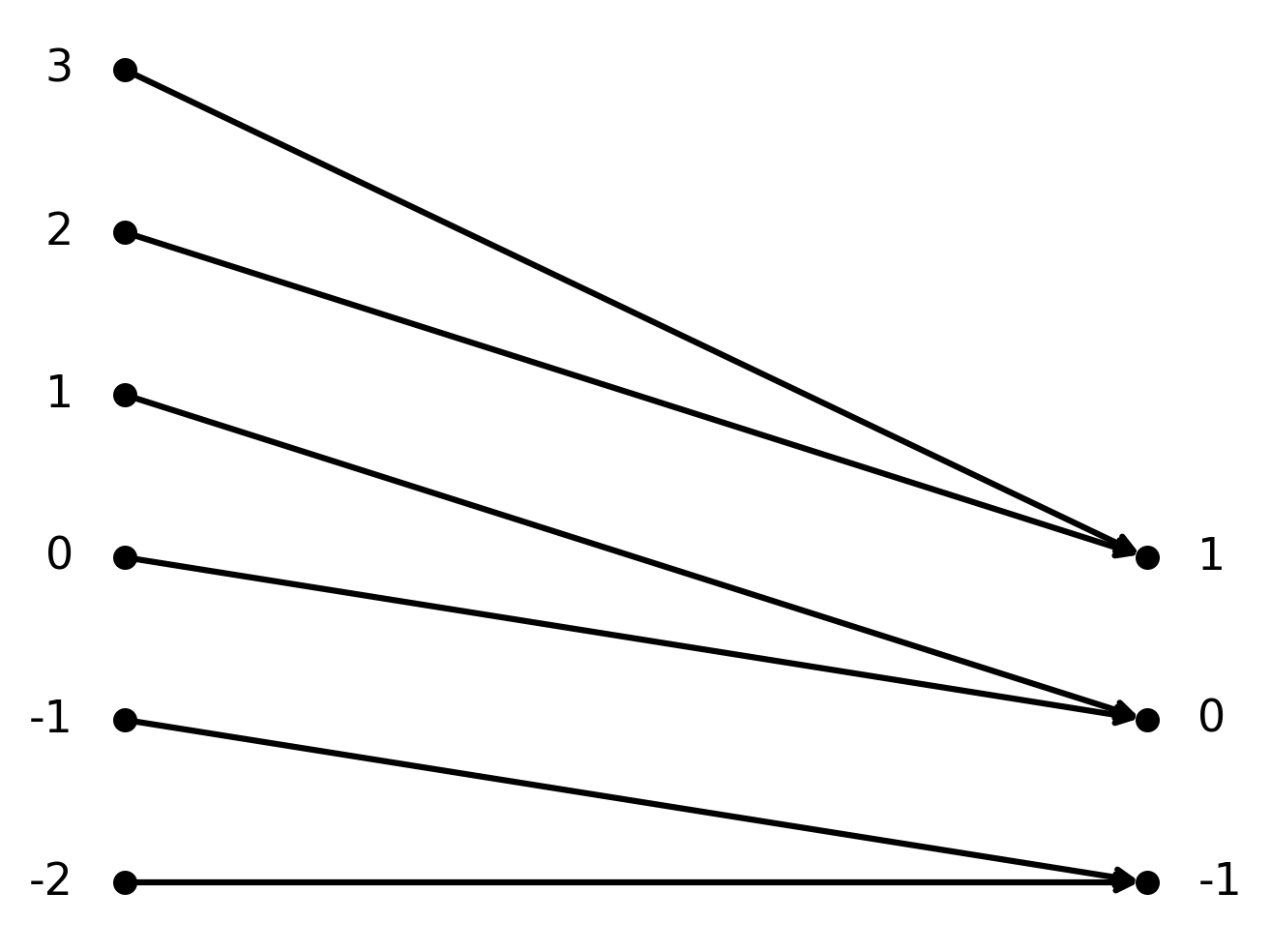
Aquí la función es sobreyectiva, porque cada número entero es alcanzado por al menos un \( \large n\). Por ejemplo, \(\large f(2)=1\) y \(\large f(3)=1\).

En cambio, la función no es inyectiva, porque varias entradas pueden dar la misma salida.

 

 

Ejemplo 3: Función biyectiva en \( \large \mathbb{Z}\)

La función \( \large f : \mathbb{Z} \to \mathbb{Z}\) dada por \( \large f(n) = n+1\).

 

$$ \large f(n) = n+1 $$

 

 

Aquí \(\large f\) es biyectiva: cada número entero obtiene una salida única, y todos los enteros son alcanzados.

Así, la función puede invertirse con una inversa \(\large f^{-1}(n) = n-1\).

 

 

Ejemplo 4: Funciones en \( \large \mathbb{R}\)

En los números reales, podemos encontrar muchas funciones que ilustran las propiedades:

 

• \( \large f(x) = x^3 \) de \( \large \mathbb{R} \to \mathbb{R}\) es biyectiva. Cada número real tiene una imagen única y todo \( \large \mathbb{R}\) queda cubierto.
• \( \large f(x) = x^2 \) de \( \large \mathbb{R} \to \mathbb{R}\) no es inyectiva (porque \( f(2)=f(-2)\)), pero es sobreyectiva si solo se considera \( \large [0,\infty[\) como codominio.
• \( \large f(x) = e^x \) de \( \large \mathbb{R} \to (0,\infty)\) es biyectiva, porque todos los números reales positivos son alcanzados de manera única.

 

 

Resumen

Los ejemplos muestran que las propiedades de las funciones dependen de:

 

• Qué conjuntos consideramos como dominio y codominio.
• Cómo la función relaciona entrada y salida.

 

Los conjuntos numéricos clásicos \( \large \mathbb{N}, \mathbb{Z}, \mathbb{R}\) proporcionan muchos buenos y sencillos ejemplos de funciones inyectivas, sobreyectivas y biyectivas.