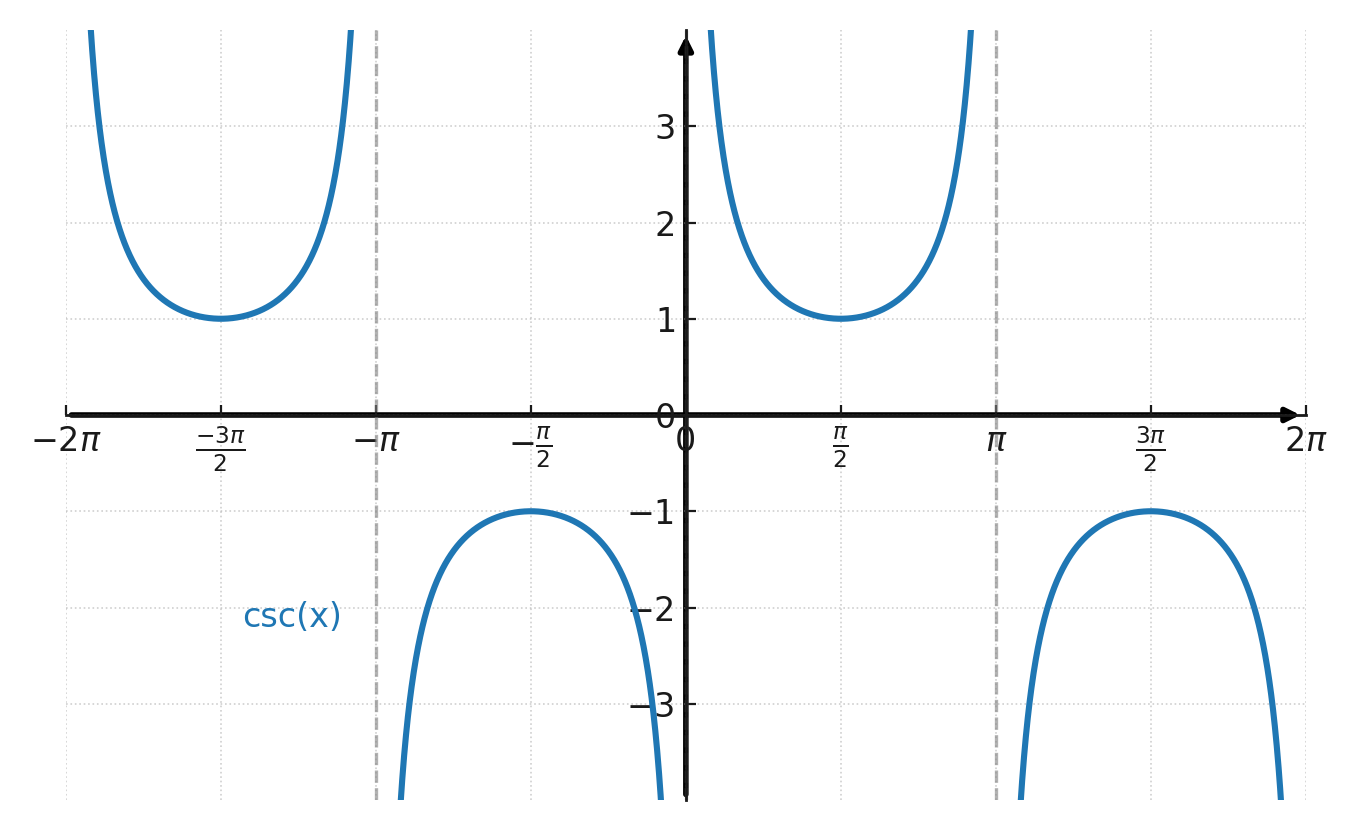
Secante y cosecante
También existen dos funciones recíprocas, llamadas secante y cosecante. Se definen como los valores inversos del coseno y del seno:
$$ \large \sec(v) = \tfrac{1}{\cos(v)} \qquad \csc(v) = \tfrac{1}{\sin(v)} $$
Esto significa que si conoces el coseno o el seno de un ángulo, puedes encontrar la secante o la cosecante simplemente tomando el valor recíproco.
Por ejemplo, si el ángulo es de 25°:
$$ \large \cos(25^\circ) \approx 0.906 \quad \Rightarrow \quad \sec(25^\circ) \approx 1.103 $$
$$ \large \sin(25^\circ) \approx 0.423 \quad \Rightarrow \quad \csc(25^\circ) \approx 2.366 $$
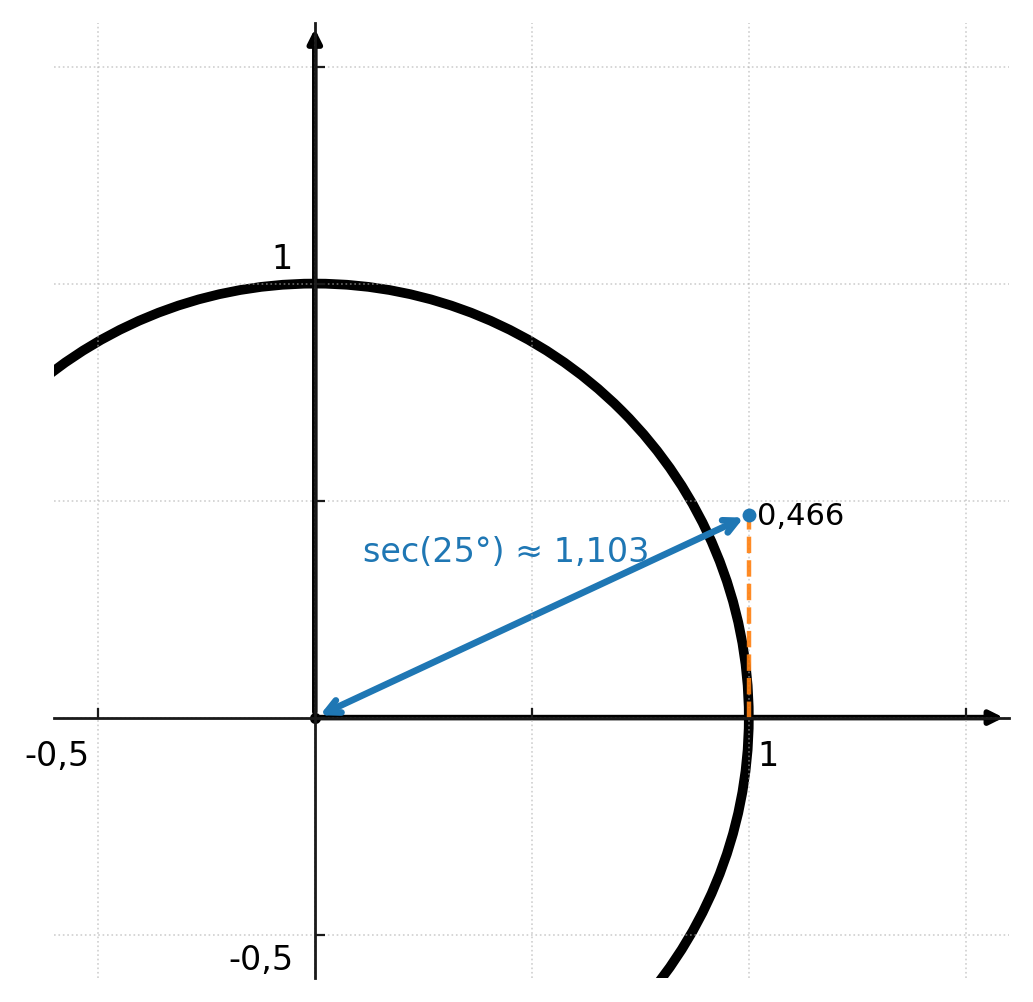
En el círculo unitario, la secante y la cosecante también se pueden ilustrar gráficamente.
Ambas funciones se encuentran extendiendo el rayo del ángulo hasta que corta la línea x = 1 (para la secante) y la línea y = 1 (para la cosecante).
La distancia desde el centro hasta el punto de intersección es el valor de la función. La figura de abajo muestra que la tangente es 0,466 y la secante es 1,103.
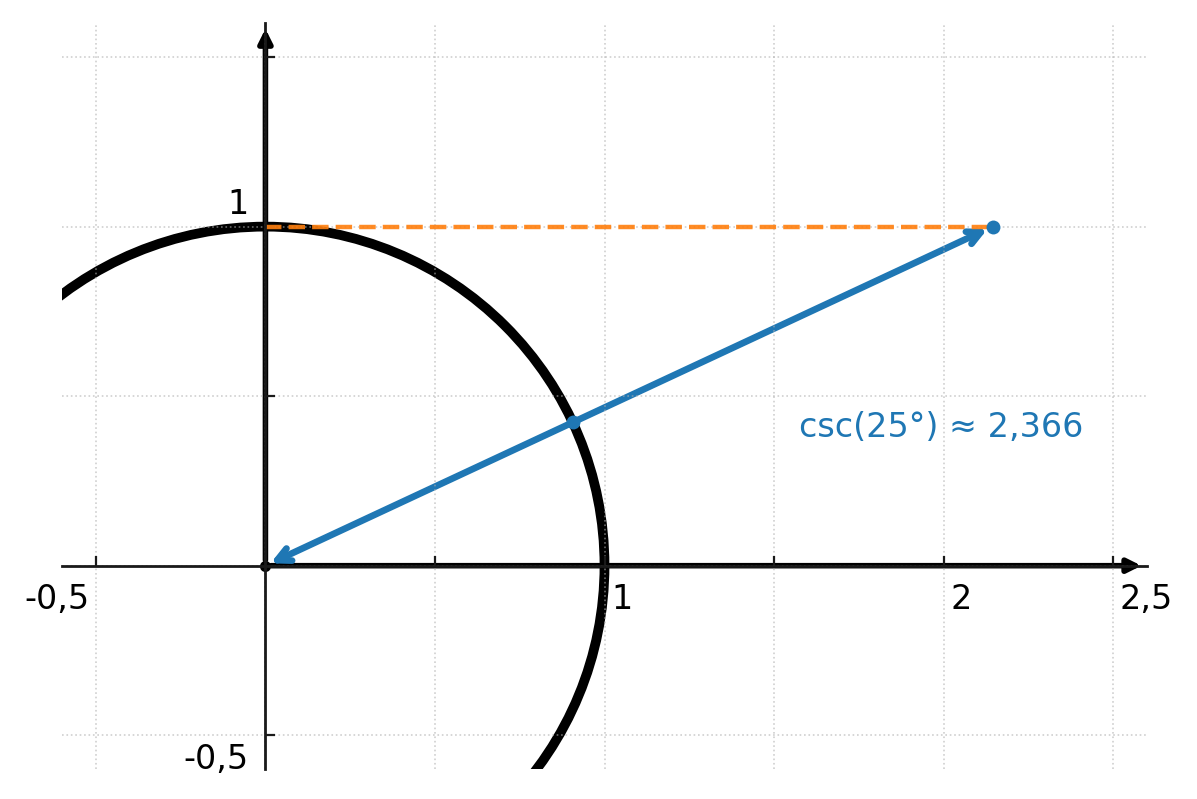
Aquí se muestra la cosecante en el círculo unitario para el ángulo de 25 grados, donde la longitud desde el centro hasta el punto de intersección es 2,366
Aplicación
La secante y la cosecante son más útiles, por ejemplo, en el cálculo diferencial y en otras áreas avanzadas de las matemáticas, donde simplifican ciertos cálculos.
En la geometría elemental normalmente se utilizan solo el seno, el coseno y la tangente.
Una mirada rápida a las gráficas de la secante y la cosecante explica por qué. Las funciones tienen asíntotas verticales, saltan a valores muy grandes y no están definidas en todas partes, a diferencia del seno y el coseno.
Gráfico de la secante:
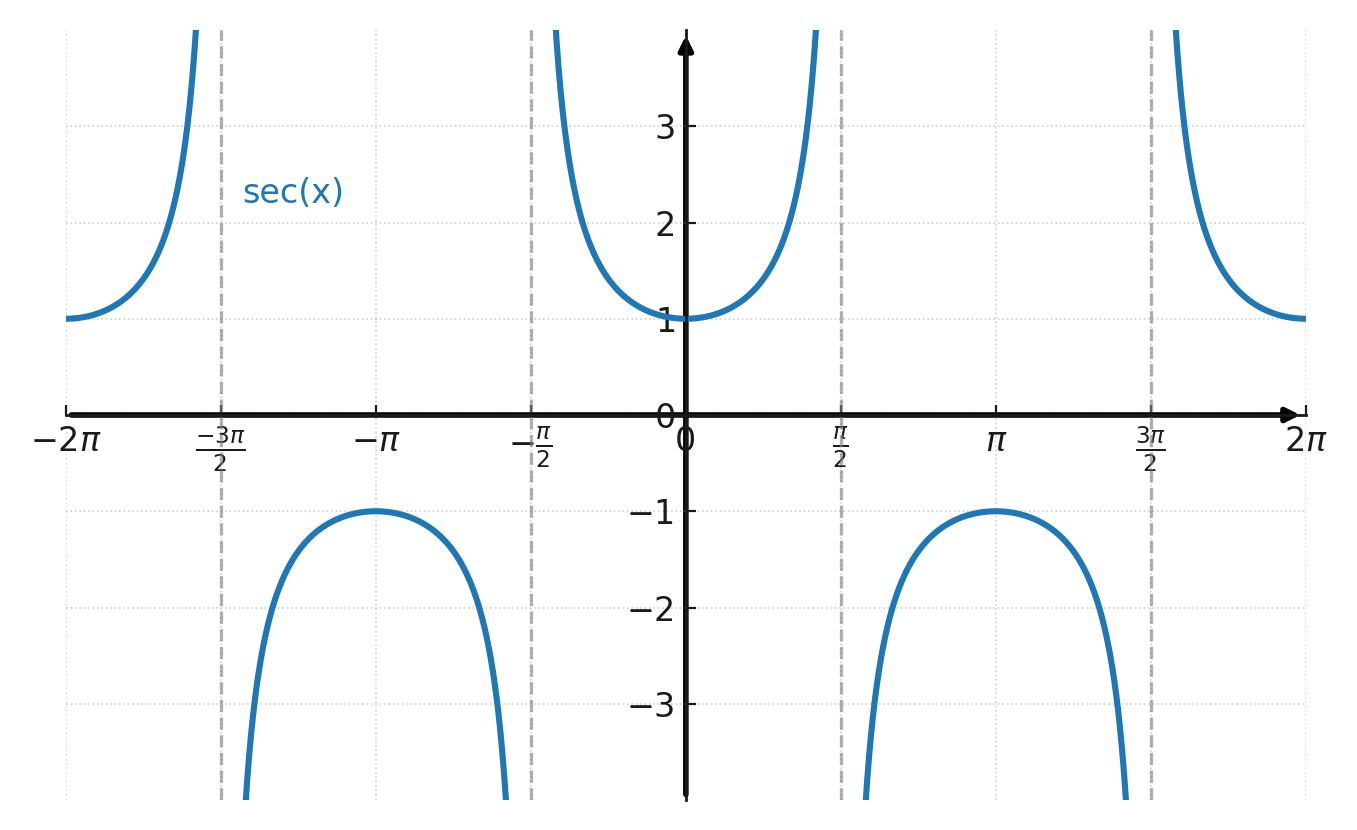
Gráfico de la cosecante: