Tangente y cotangente
La tangente es también una función trigonométrica que nos dice algo sobre el ángulo en el círculo unitario. A diferencia del coseno y el seno, el resultado puede ser mayor que 1.
La definición de la tangente es:
$$ tan(v) = \frac{sin(v)}{cos(v)} $$
Esto significa que un ángulo (A) de 25 grados se calcula así:
$$ tan(v) = \frac{sin(v)}{cos(v)} \qquad \Leftrightarrow $$
$$ tan(v) = \frac{sin(25^\circ)}{cos(25^\circ)} \qquad \Leftrightarrow $$
$$ tan(v) = \frac{0.423}{0.906} \qquad \Leftrightarrow $$
$$ tan(v) \approx 0.467 $$
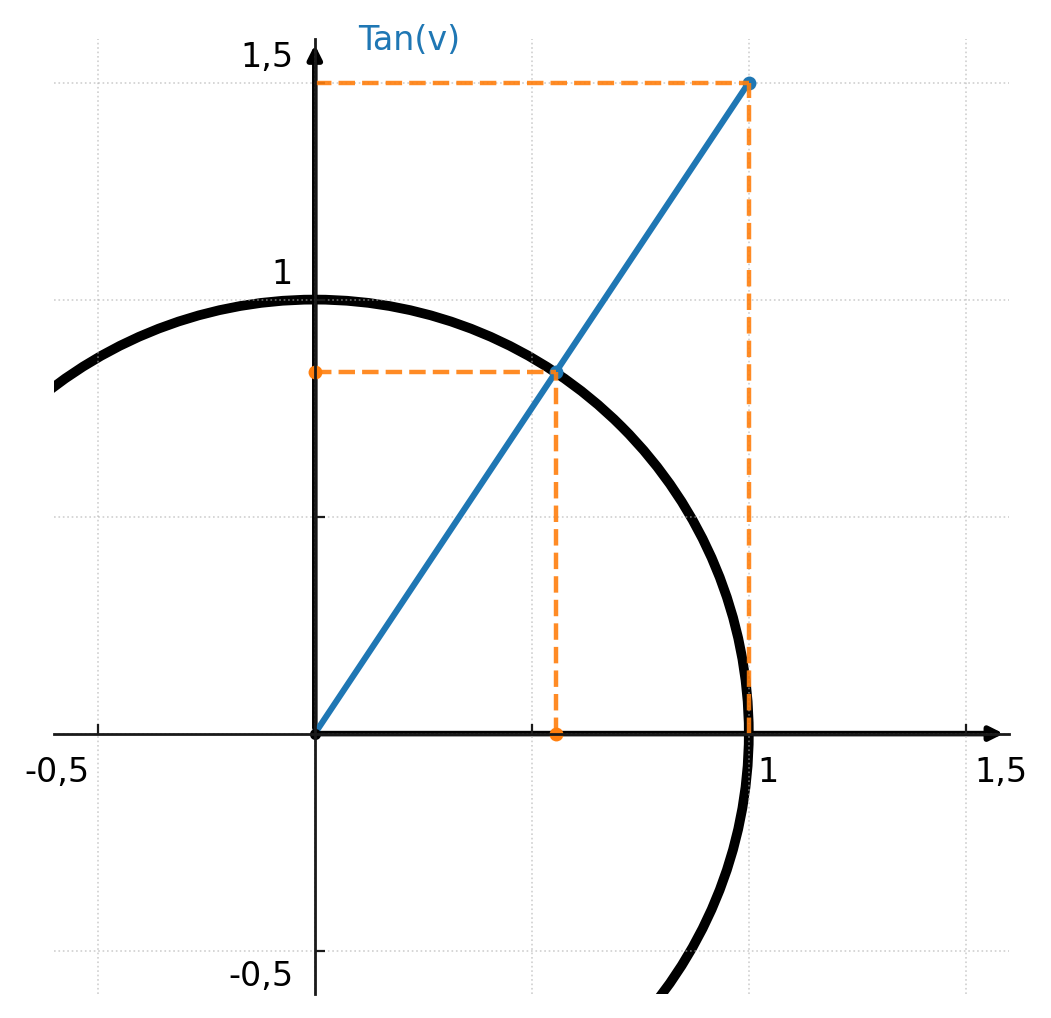
La tangente también puede leerse en el círculo unitario. Se comienza dibujando una línea vertical tangente al círculo unitario en el punto \((1, 0)\).
Así se puede ver dónde el ángulo corta la línea. La coordenada y del punto de intersección es la tangente del ángulo.
Cotangente
La cotangente es el recíproco de la tangente:
$$ cot(v) = \frac{cos(v)}{sin(v)} $$
La cotangente no se usa con tanta frecuencia, porque el seno, el coseno y la tangente permiten realizar los cálculos geométricos más comunes.
Tampoco suele encontrarse un botón de cot en las calculadoras comunes.
En el círculo unitario, la cotangente se traza horizontalmente desde el punto \((0,1)\) y se lee en el eje x donde corta al ángulo:
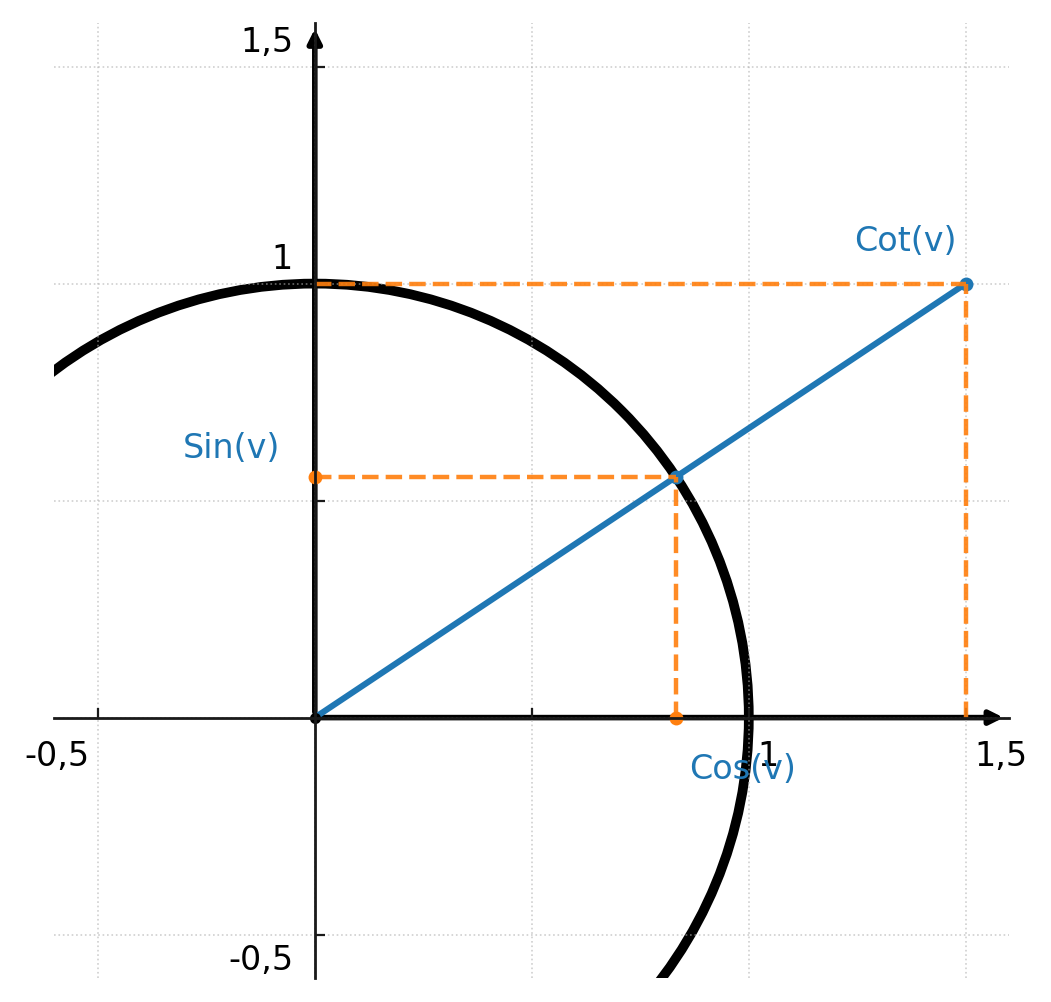
El ángulo de 25 grados se calcula así:
$$ cot(v) = \frac{cos(v)}{sin(v)} \qquad \Leftrightarrow $$
$$ cot(v) = \frac{cos(25^\circ)}{sin(25^\circ)} \qquad \Leftrightarrow $$
$$ cot(v) = \frac{0.906}{0.423} \qquad \Leftrightarrow $$
$$ cot(v) \approx 2.14 $$
Funciones inversas
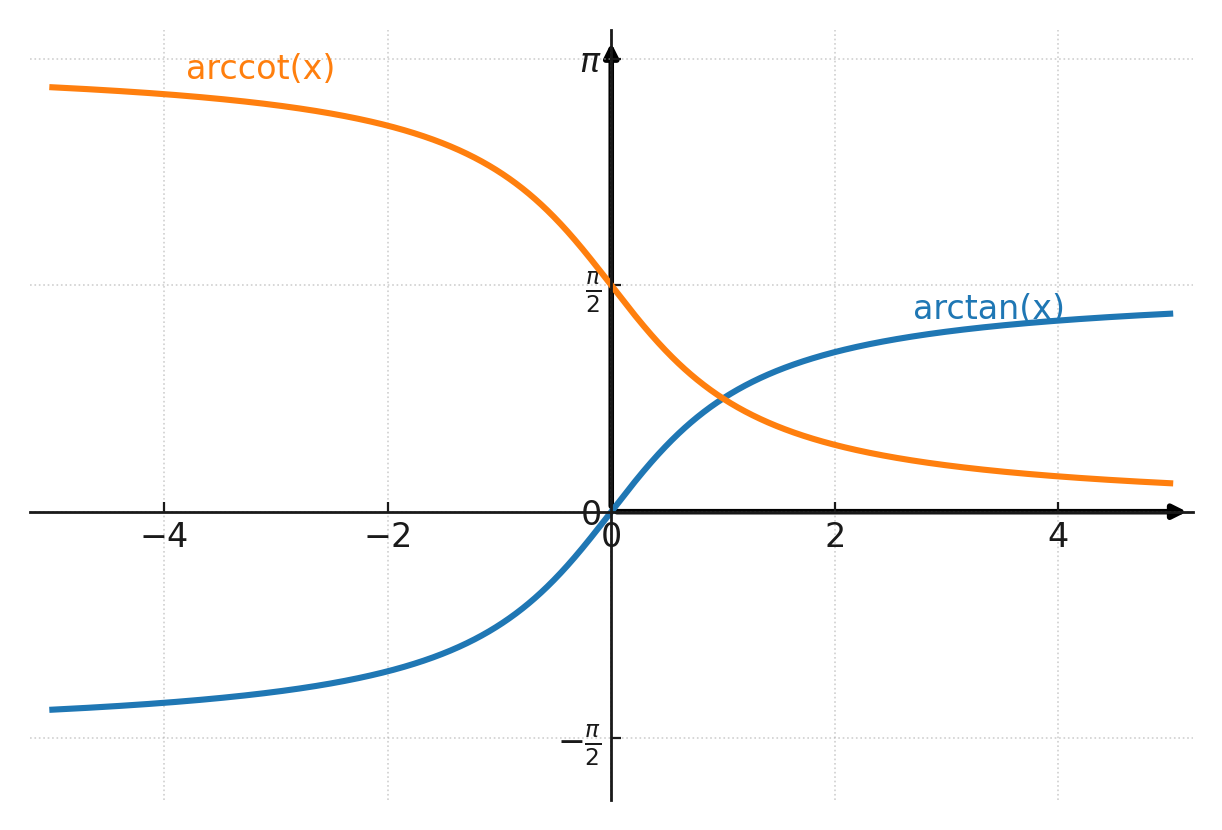
Al igual que arcsin y arccos, también existen funciones inversas para la tangente y la cotangente. Estas se llaman arctan y arccot (o se escriben como tan-1 y cot-1).
Si conoces la tangente de un ángulo, pero no el ángulo mismo, puedes hallarlo con arctan. Por ejemplo, sabemos que:
$$ tan(45^\circ) = 1 $$
Entonces también se cumple que:
$$ tan^{-1}(1) = 45^\circ $$
Arctan puede usarse para calcular un ángulo a partir de la razón entre dos lados en un triángulo rectángulo.
Arccot funciona de la misma manera para la cotangente. Si conoces la cotangente de un ángulo, puedes hallar el ángulo con arccot. Por ejemplo:
$$ cot(45^\circ) = 1 \qquad \Leftrightarrow \qquad cot^{-1}(1) = 45^\circ $$
Ambas funciones darán dos soluciones si no se restringen. Aquí se ven las dos soluciones de arctan en el primer y tercer cuadrante:
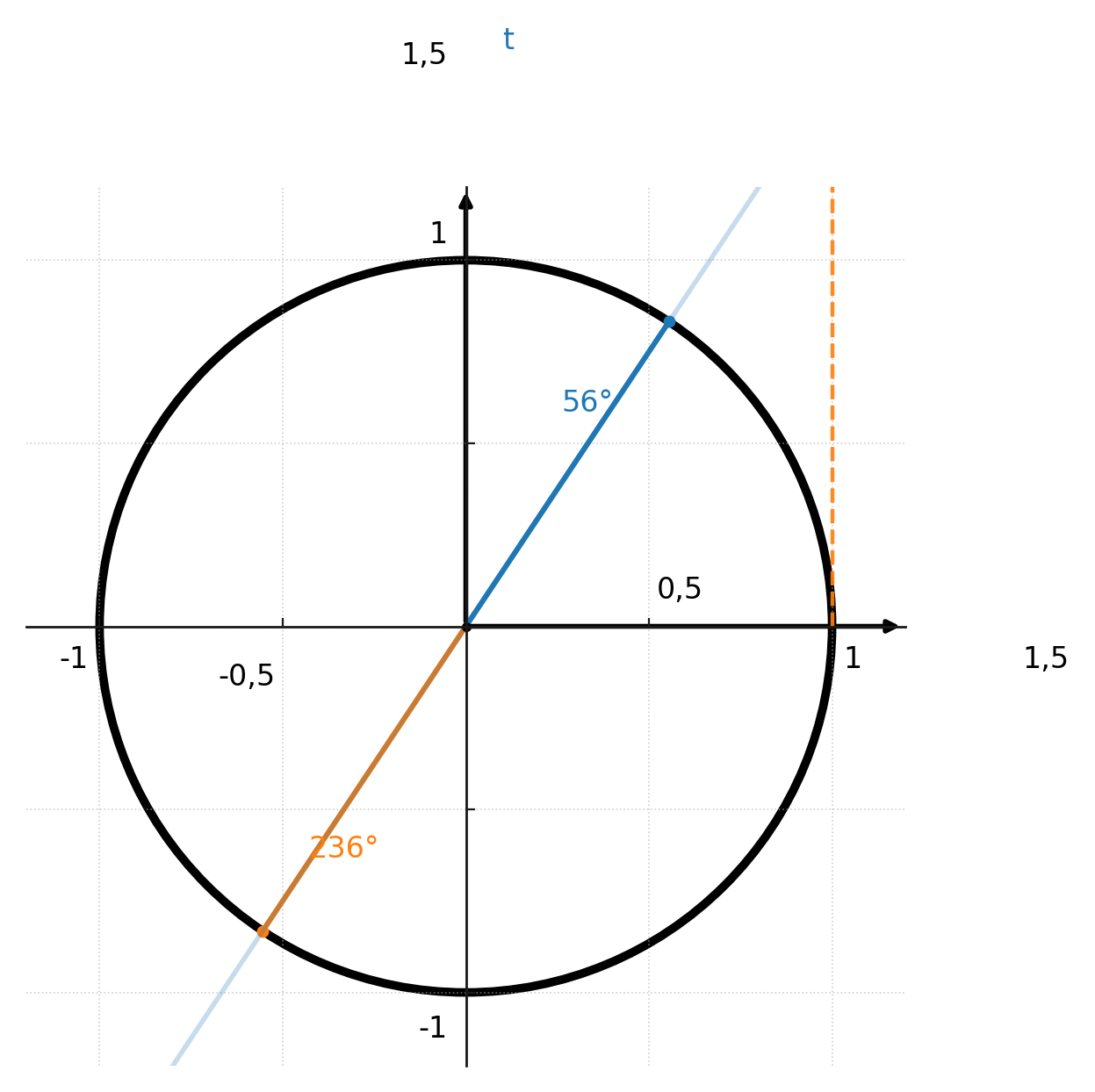
Las funciones se restringen de la siguiente manera:
- Para arctan, el ángulo se restringe al intervalo \(-90^\circ \leq v \leq 90^\circ\)
- Para arccot, el ángulo se restringe al intervalo \(0^\circ \leq v \leq 180^\circ\)
¡De esta forma, las funciones son únicas!
Las dos funciones inversas están dibujadas en el sistema de coordenadas. Ten en cuenta que el eje y está en radianes y no en grados.