Ecuaciones diferenciales

Una ecuación diferencial describe la relación entre una función y su derivada. En lugar de indicar directamente qué es la función, describe cómo cambia. Esto convierte a las ecuaciones diferenciales en una herramienta fundamental en matemáticas, física, biología y economía, donde muchos fenómenos tratan precisamente de cambios a lo largo del tiempo.

 

 

Qué es una ecuación diferencial

Una ecuación ordinaria contiene una cantidad desconocida, por ejemplo \( \large x \). En cambio, una ecuación diferencial contiene una función desconocida \( \large y(x) \) y sus derivadas, como \( \large y'(x) \) o \( \large y''(x) \). El objetivo es encontrar la función \( \large y(x) \) que satisfaga la ecuación.

 

Ejemplos:

 

$$ \large y' = 3x^2 $$

 

$$ \large y'' + y = 0 $$

 

La primera ecuación indica que la pendiente de \( \large y \) es siempre \( \large 3x^2 \). La segunda describe una oscilación, ya que relaciona la función con su propia segunda derivada.

 

 

Idea básica

Una ecuación diferencial no indica directamente cómo es la gráfica de \( \large y \), sino cómo cambia su pendiente de un punto a otro. Puede considerarse como una receta para el movimiento o el crecimiento.

 

Si se conoce la derivada, la función puede encontrarse haciendo lo contrario de derivar, es decir, integrando. Por eso, las ecuaciones diferenciales están estrechamente relacionadas con el cálculo integral.

 

 

Orden y tipos

Una ecuación diferencial ordinaria (abreviada ODE) implica solo una variable independiente, normalmente \( \large x \) o \( \large t \). Si la ecuación incluye varias variables y derivadas con respecto a varias de ellas, se llama una ecuación diferencial parcial (PDE).

 

El orden de una ecuación diferencial es la derivada de orden más alto que aparece. Por ejemplo:

 

• \( \large y' = 3x^2 \) → ecuación de primer orden
• \( \large y'' + y = 0 \) → ecuación de segundo orden

 

 

Resolución de ecuaciones diferenciales simples

Las ecuaciones diferenciales más sencillas pueden resolverse directamente mediante integración. Por ejemplo, si

 

$$ \large y' = 3x^2 $$

 

entonces \( \large y(x) \) puede obtenerse integrando el lado derecho:

 

$$ \large y = \int 3x^2 \, dx = x^3 + C $$

 

Aquí \( \large C \) es la constante de integración, que representa todas las posibles soluciones — es decir, todas las gráficas con el mismo patrón de pendiente pero diferente posición vertical.

 

 

Separación de variables

Un método común para resolver ecuaciones de primer orden es la separación de variables. Si la ecuación puede escribirse como

 

$$ \large \frac{dy}{dx} = g(x) \cdot h(y) $$

 

entonces \( \large x \) y \( \large y \) pueden separarse e integrarse en cada lado:

 

$$ \large \int \frac{1}{h(y)} \, dy = \int g(x) \, dx $$

 

Ejemplo: Resolver \( \large y' = 2xy \).

 

Separar las variables: \( \large \frac{1}{y} dy = 2x dx \).

 

Integrar ambos lados:

 

$$ \large \ln|y| = x^2 + C $$

 

Reescribir la solución general:

 

$$ \large y = A e^{x^2} $$

 

donde \( \large A = e^C \) es una constante. Este método funciona siempre que las variables puedan separarse de esta manera.

 

 

Ecuaciones diferenciales lineales de primer orden

Una ecuación lineal de primer orden tiene la forma:

 

$$ \large y' + p(x)y = q(x) $$

 

La solución se encuentra multiplicando toda la ecuación por un factor integrante:

 

$$ \large \mu(x) = e^{\int p(x)\,dx} $$

 

Así, la ecuación puede escribirse como

 

$$ \large (\mu(x)y)' = \mu(x)q(x) $$

 

y luego integrarse directamente. Este método se conoce como el método del factor integrante.

 

 

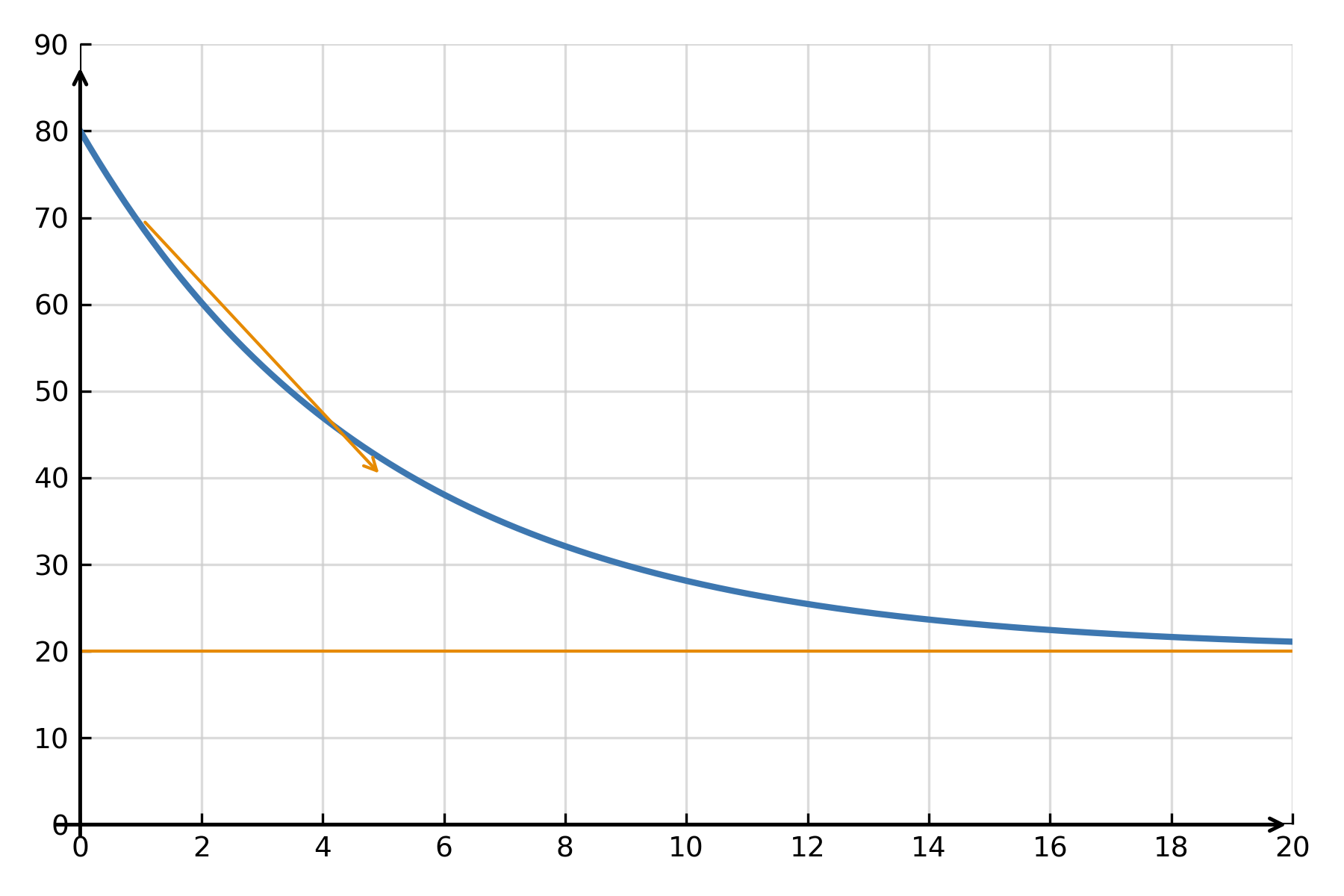
Ejemplo: Ley del enfriamiento de Newton

Un ejemplo clásico de una ecuación diferencial lineal es la ley del enfriamiento de Newton:

 

$$ \large \frac{dT}{dt} = -k(T - T_{\text{amb}}) $$

 

Aquí \( \large T(t) \) representa la temperatura de un objeto que se enfría hacia la temperatura ambiente \( \large T_{\text{amb}} \), y \( \large k \) es una constante. La solución muestra que la temperatura se aproxima exponencialmente a la del entorno:

 

$$ \large T(t) = T_{\text{amb}} + (T_0 - T_{\text{amb}})e^{-kt} $$

 

Este tipo de ecuación también aparece en la desintegración radiactiva, la descarga de condensadores y los modelos económicos de ajuste.

 

 

 

Ecuaciones diferenciales de segundo orden

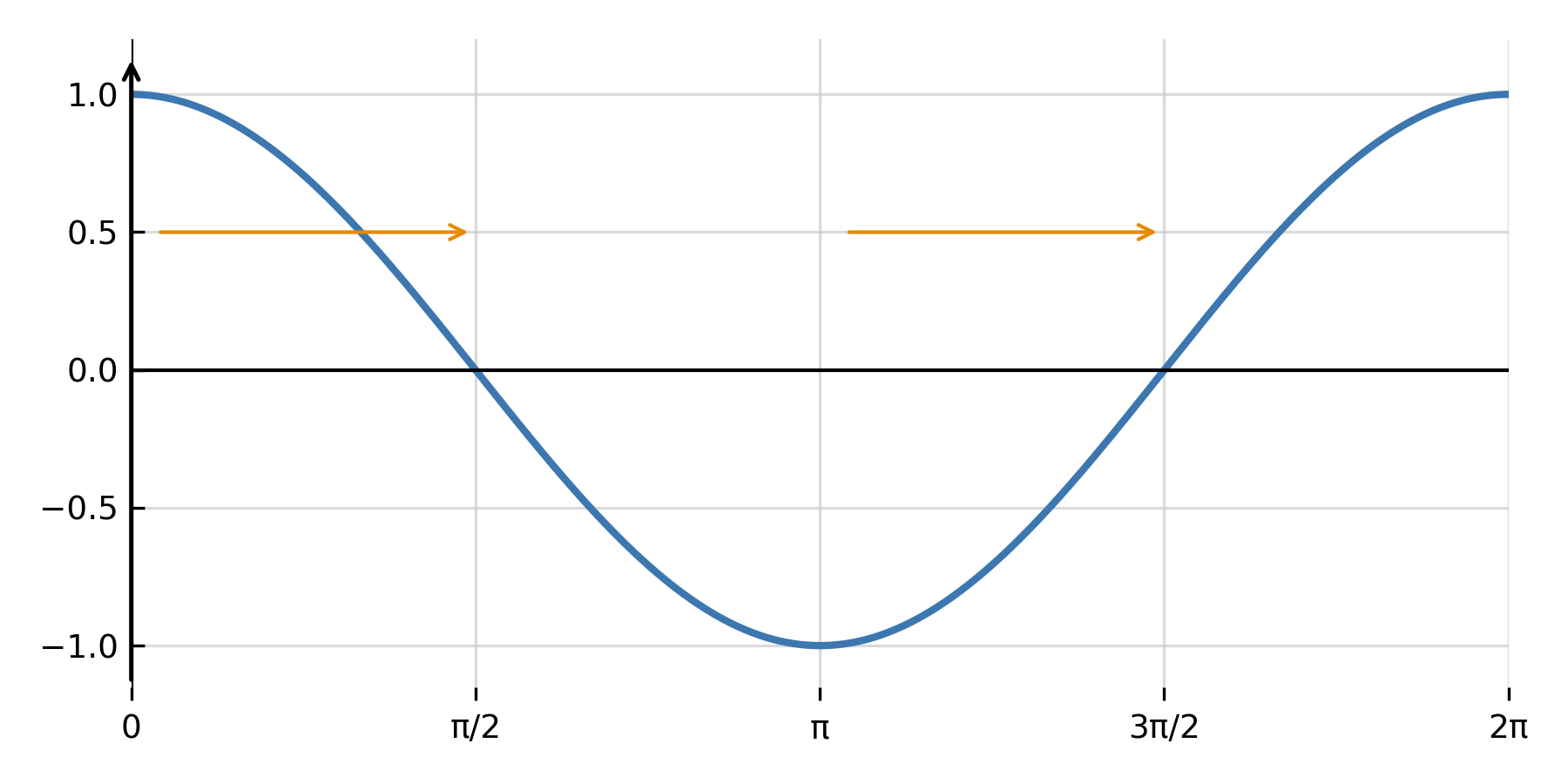
Cuando interviene la segunda derivada, la ecuación suele describir movimiento u oscilaciones. Un ejemplo importante es la oscilación armónica:

 

$$ \large y'' + \omega^2 y = 0 $$

 

La solución es una combinación de seno y coseno:

 

$$ \large y = A \cos(\omega x) + B \sin(\omega x) $$

 

Aquí \( \large A \) y \( \large B \) representan las condiciones iniciales, mientras que \( \large \omega \) indica la frecuencia de oscilación. Este tipo de ecuación se utiliza en mecánica, ondas y circuitos eléctricos.

 

 

 

Soluciones numéricas

En muchos casos, una ecuación diferencial no puede resolverse de forma analítica. En su lugar, se emplean métodos numéricos, en los que la función se calcula punto por punto a partir de su derivada. Los métodos más conocidos son el método de Euler, Runge–Kutta y el método de la secante, todos explicados en la sección Métodos numéricos.

 

 

Resumen

Las ecuaciones diferenciales describen cómo cambian las funciones y desempeñan un papel central en las matemáticas aplicadas. Se utilizan para modelar el crecimiento, el movimiento, las oscilaciones, el calor, la corriente y muchos otros fenómenos. Algunas pueden resolverse manualmente, mientras que otras requieren métodos numéricos, pero todas conectan el cálculo diferencial y el cálculo integral en un sistema unificado.