Continuidad
Al hablar del comportamiento de las funciones, uno de los conceptos más importantes es la continuidad. La continuidad describe si una función cambia de manera suave o si aparecen saltos, huecos o cambios bruscos en la gráfica. Una función continua puede dibujarse sin levantar el lápiz del papel.
Definición de continuidad
Una función \( \large f(x) \) es continua en un punto \( \large x = a \) si el límite de la función en ese punto es igual al valor de la función. Se escribe como:
$$ \large \lim_{x \to a} f(x) = f(a) $$
Para que una función sea continua en un punto, deben cumplirse tres condiciones:
- La función está definida en \( \large a \)
- Existe el límite \( \large \lim_{x \to a} f(x) \)
- Ambos valores son iguales
Si una de estas condiciones no se cumple, la función no es continua en ese punto.
Tipos de discontinuidad
Existen varias formas en que una función puede ser discontinua. Los tipos principales son:
| Tipo | Descripción |
|---|---|
| Discontinuidad por salto | La función salta repentinamente de un valor a otro. |
| Hueco | El límite existe, pero la función no está definida en ese punto. |
| Discontinuidad infinita | La función crece sin límite en el punto (por ejemplo, cerca de una asíntota vertical). |
Estos tipos pueden observarse claramente en la gráfica y ayudan a comprender el comportamiento general de la función. El ejemplo siguiente muestra una discontinuidad por salto:
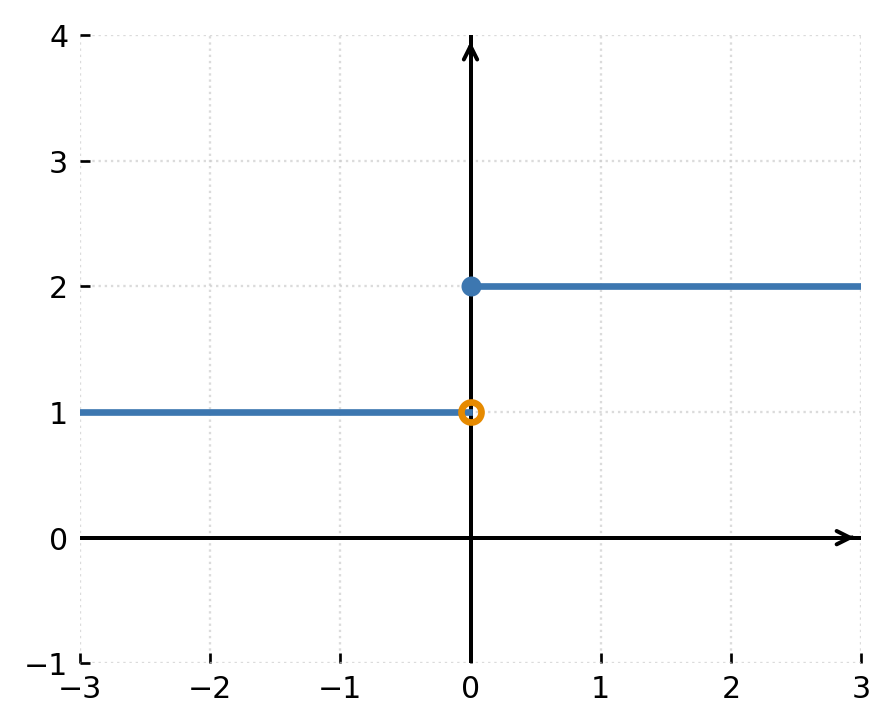
Ejemplos
1: La función \( \large f(x) = 2x + 1 \) es continua en todo su dominio, ya que puede sustituirse cualquier valor de x sin interrumpir la gráfica.
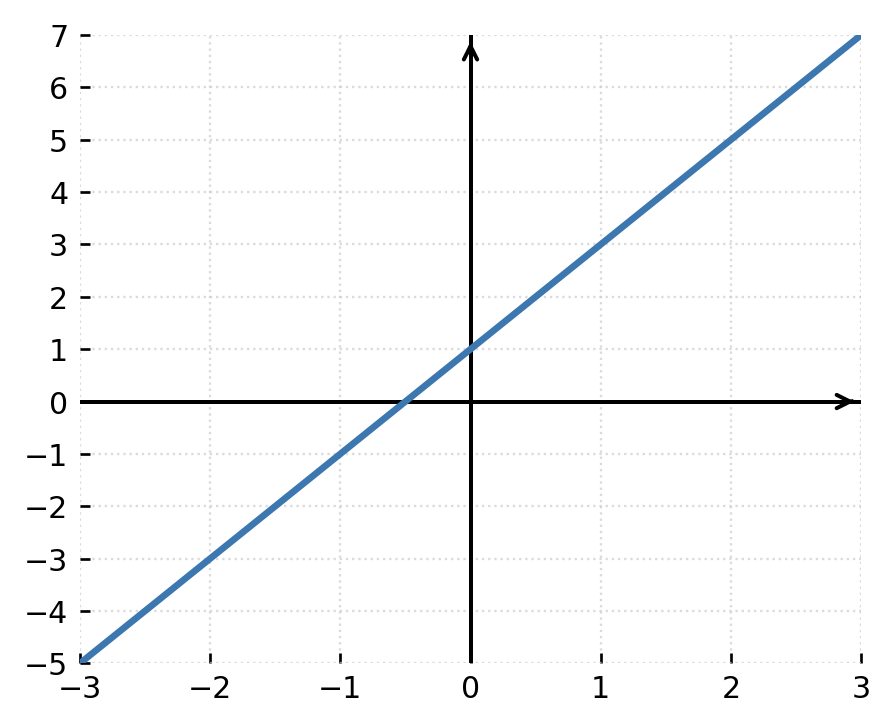
2: La función
$$ \large f(x) = \frac{x^2 - 9}{x - 3} $$
no está definida en \( \large x = 3 \), pero el límite en ese punto existe:
$$ \large \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = 6 $$
Por tanto, la gráfica tiene un hueco en el punto (3, 6). La función puede hacerse continua definiendo \( \large f(3) = 6 \).
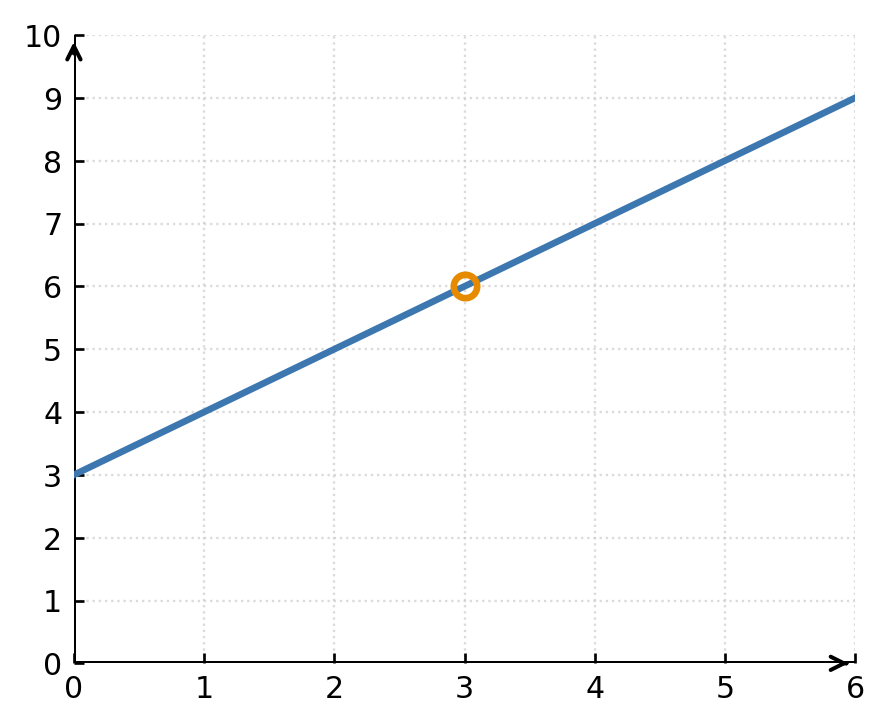
Continuidad en un intervalo
Una función se dice continua en un intervalo si es continua en cada punto de ese intervalo. Los polinomios, las funciones exponenciales, logarítmicas y trigonométricas son ejemplos de funciones continuas en todo su dominio.
La continuidad es un requisito importante para muchos teoremas del análisis, como el teorema del valor intermedio y los teoremas sobre derivabilidad.
Importancia en el análisis
La continuidad garantiza que los pequeños cambios en x produzcan pequeños cambios en f(x). Esta propiedad es esencial para definir la derivada, que describe la pendiente de la función y sus cambios locales. La continuidad es, por tanto, una base fundamental de todo el análisis.