Dot product and angles

The dot product is a way of combining two vectors that gives a number. It is used, among other things, to determine the angle between two vectors and to decide whether they are perpendicular.

 

Definition

For two vectors \( \large \mathbf{u} = (x_1,y_1) \) and \( \large \mathbf{v} = (x_2,y_2) \), we have:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1 \cdot x_2 + y_1 \cdot y_2 $$

 

In addition, the dot product can be written as:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

where \( \large \theta \) is the angle between the vectors.

 

 

Examples

Example 1:

 

$$ \large \mathbf{u} = (1,0), \; \mathbf{v} = (0,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 0 + 0 \cdot 1 = 0 $$

 

The vectors are orthogonal (perpendicular), and the angle is \( \large 90^\circ \).

 

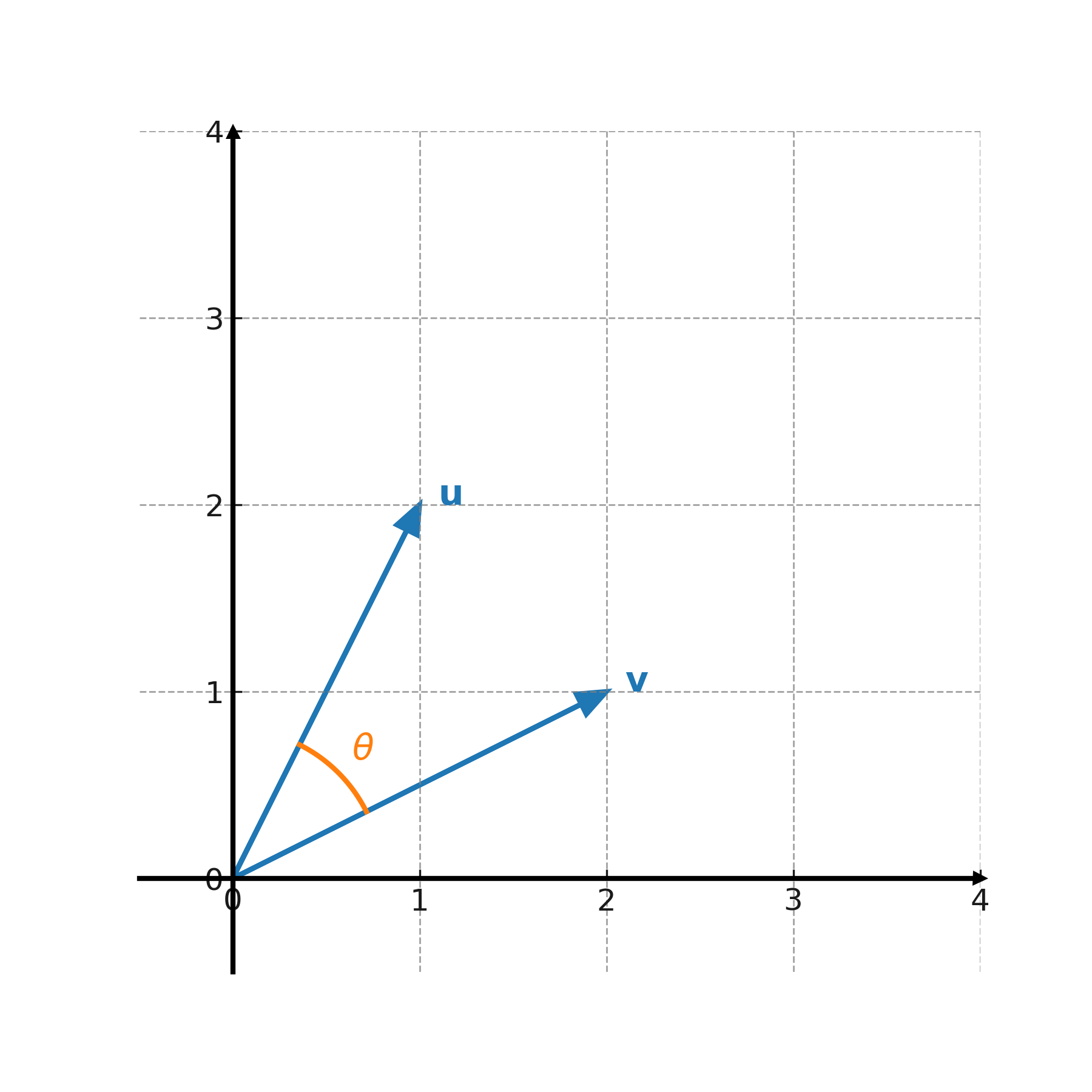
Example 2:

 

$$ \large \mathbf{u} = (1,2), \; \mathbf{v} = (2,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 2 + 2 \cdot 1 = 4 $$

 

The lengths are \( \large |\mathbf{u}| = \sqrt{5}, \; |\mathbf{v}| = \sqrt{5} \). Thus:

 

$$ \large \cos(\theta) = \frac{4}{\sqrt{5} \cdot \sqrt{5}} = \frac{4}{5} $$

 

The angle is therefore:

 

$$ \large \theta = \cos^{-1}\left(\frac{4}{5}\right) \approx 36.9^\circ $$

 

 

Geometric interpretation

The dot product measures how much of one vector points in the same direction as the other. If the angle is acute, the product is positive. If the angle is obtuse, the product is negative. If the angle is right, the product is zero.

 

 

Application

The dot product is used in mathematics and physics to determine angles and to decide whether vectors are perpendicular. In physics, it is also used to calculate the component of a force that acts in a specific direction.