Area with vectors

The area of a figure can be calculated using vectors. In particular, parallelograms and triangles can be expressed with a simple formula when described by two vectors.

 

 

Area of parallelogram and triangle

For two vectors \( \large \mathbf{u} \) and \( \large \mathbf{v} \) in the plane, the area of the parallelogram spanned by them is:

 

$$ \large A = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

 

where \( \large \theta \) is the angle between the vectors. The formula comes from calculating base times height, where the height is found as the projection of one vector onto a direction perpendicular to the other.

 

Another method is to use the determinant:

 

$$ \large A = \left| \det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \right| $$

 

if \( \large \mathbf{u} = (x_1,y_1) \) and \( \large \mathbf{v} = (x_2,y_2) \).

 

 

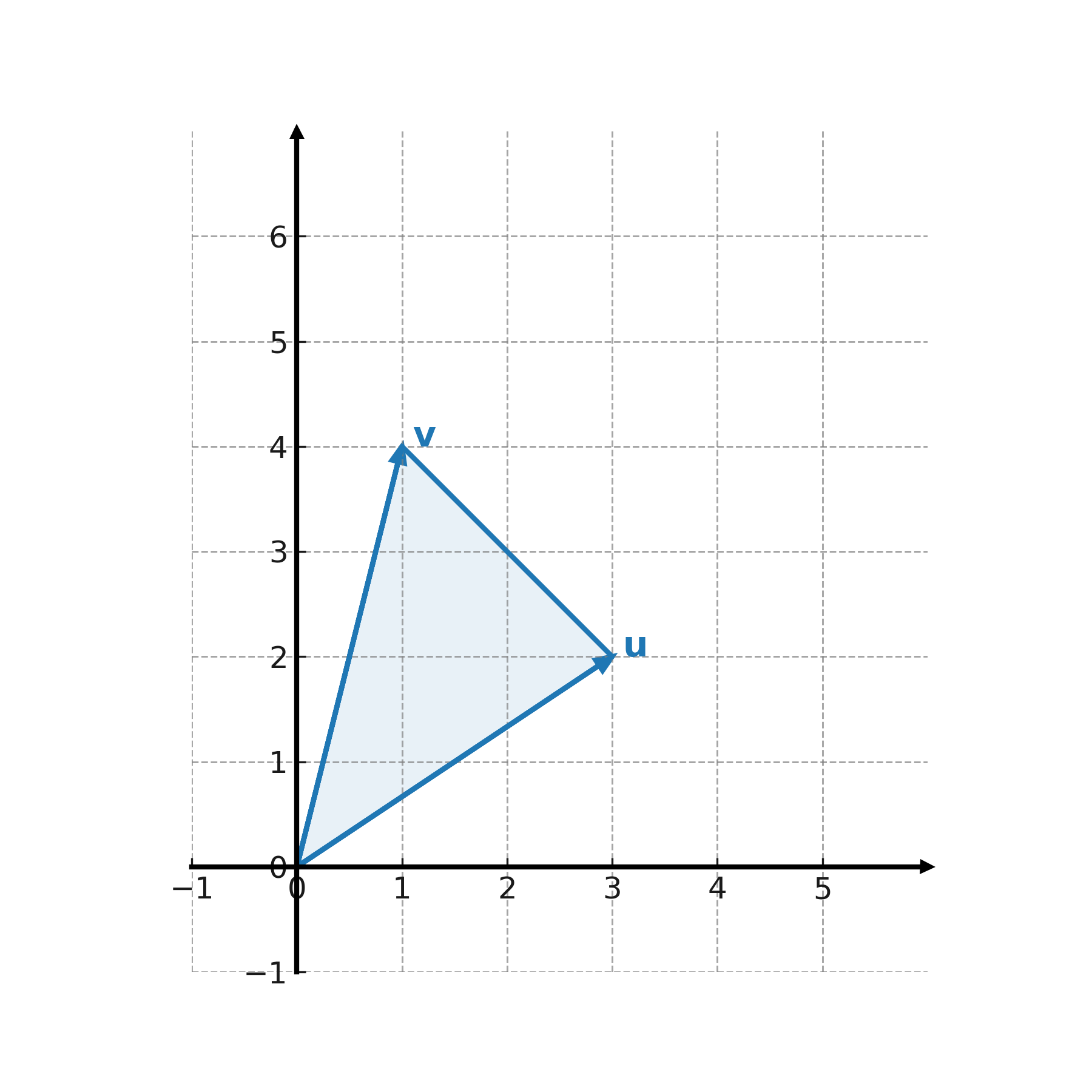
Example

We take \( \large \mathbf{u} = (3,2) \) and \( \large \mathbf{v} = (1,4) \).

 

$$ \large A = \left| \det \begin{pmatrix} 3 & 1 \\ 2 & 4 \end{pmatrix} \right| = |3 \cdot 4 - 2 \cdot 1| = |10| = 10 $$

 

The area of the parallelogram is 10. 

The area of the triangle spanned by the same two vectors is half, that is \( \large 5 \).

 

 

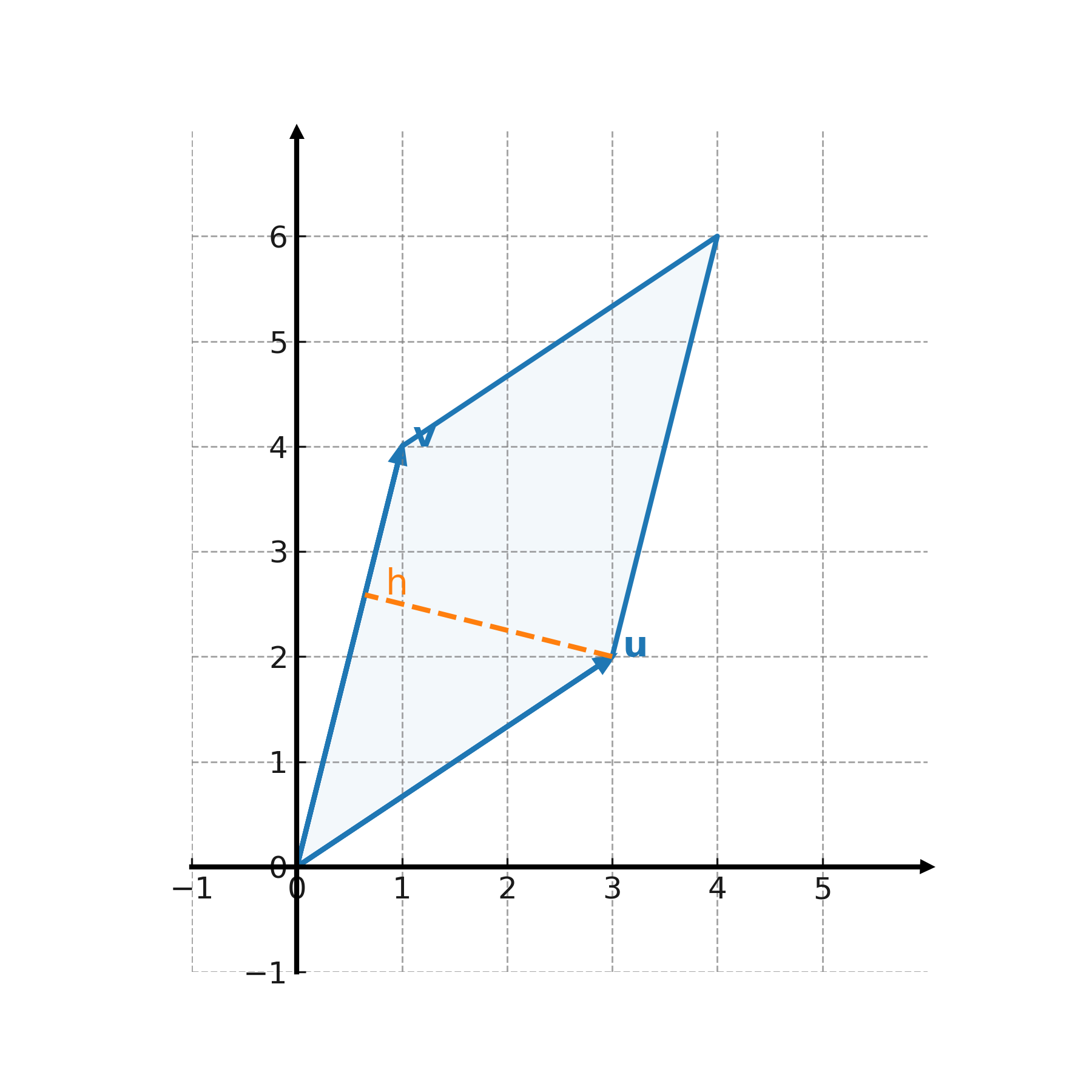
Geometric interpretation

The key point to note is that the area can be calculated as base times height, and that the height can be found using projection. Thus, the concept of projection is closely related to area calculation.

 

 

Application

Vector-based formulas for areas are used in both geometry and linear algebra. They provide a simple method for calculating areas in coordinate systems and form the basis for further topics such as determinants and volume.