Secant and cosecant

There are also two reciprocal functions, namely secant and cosecant. They are defined as the inverse values of cosine and sine:

 

$$ \large \sec(v) = \tfrac{1}{\cos(v)} \qquad \csc(v) = \tfrac{1}{\sin(v)} $$

 

This means that if you know the cosine or sine of an angle, you can find the secant or cosecant simply by taking the reciprocal value.

For example, if the angle is 25°:

 

$$ \large \cos(25^\circ) \approx 0.906 \quad \Rightarrow \quad \sec(25^\circ) \approx 1.103 $$

$$ \large \sin(25^\circ) \approx 0.423 \quad \Rightarrow \quad \csc(25^\circ) \approx 2.366 $$

 

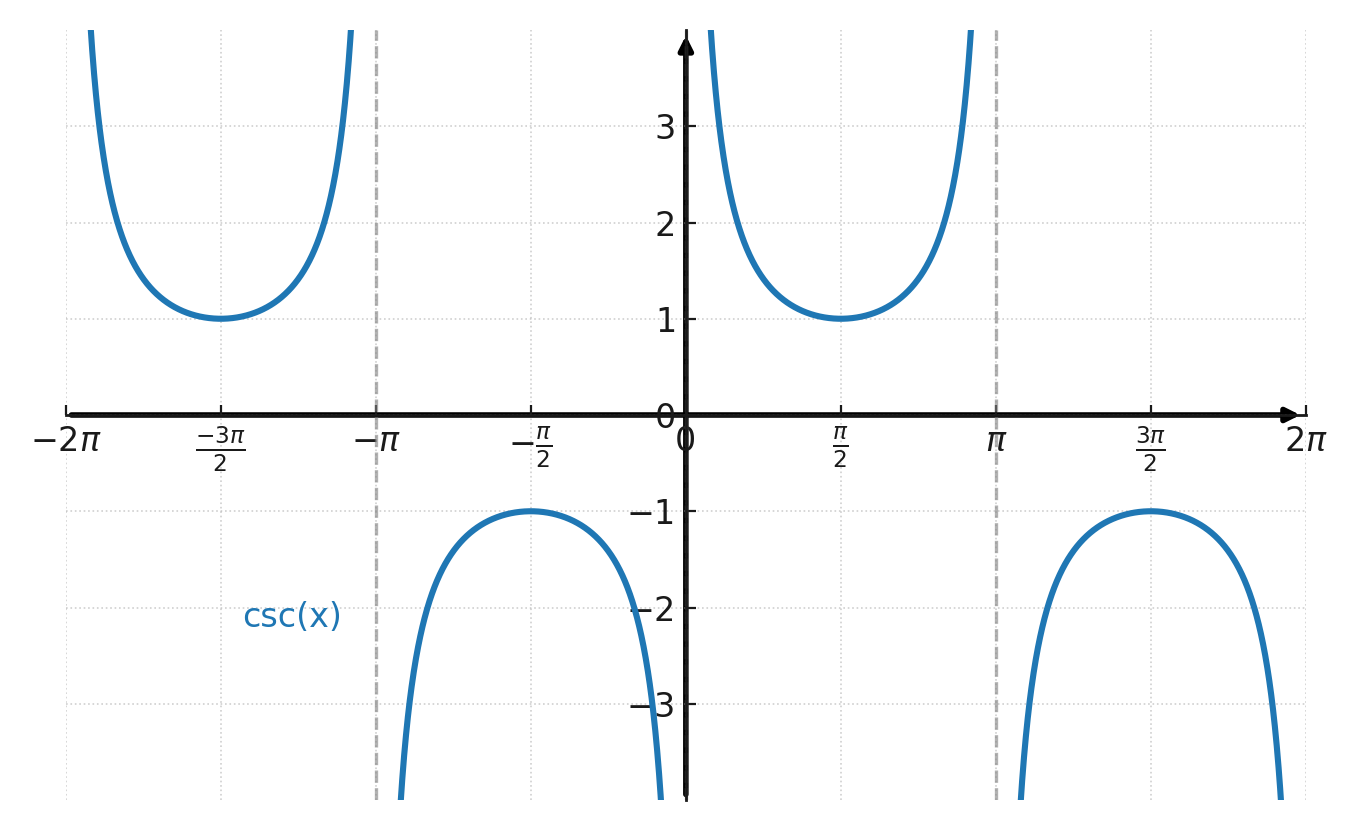
In the unit circle, secant and cosecant can also be illustrated graphically.

Both functions are found by extending the angle ray until it intersects the line x = 1 (for secant) and the line y = 1 (for cosecant).

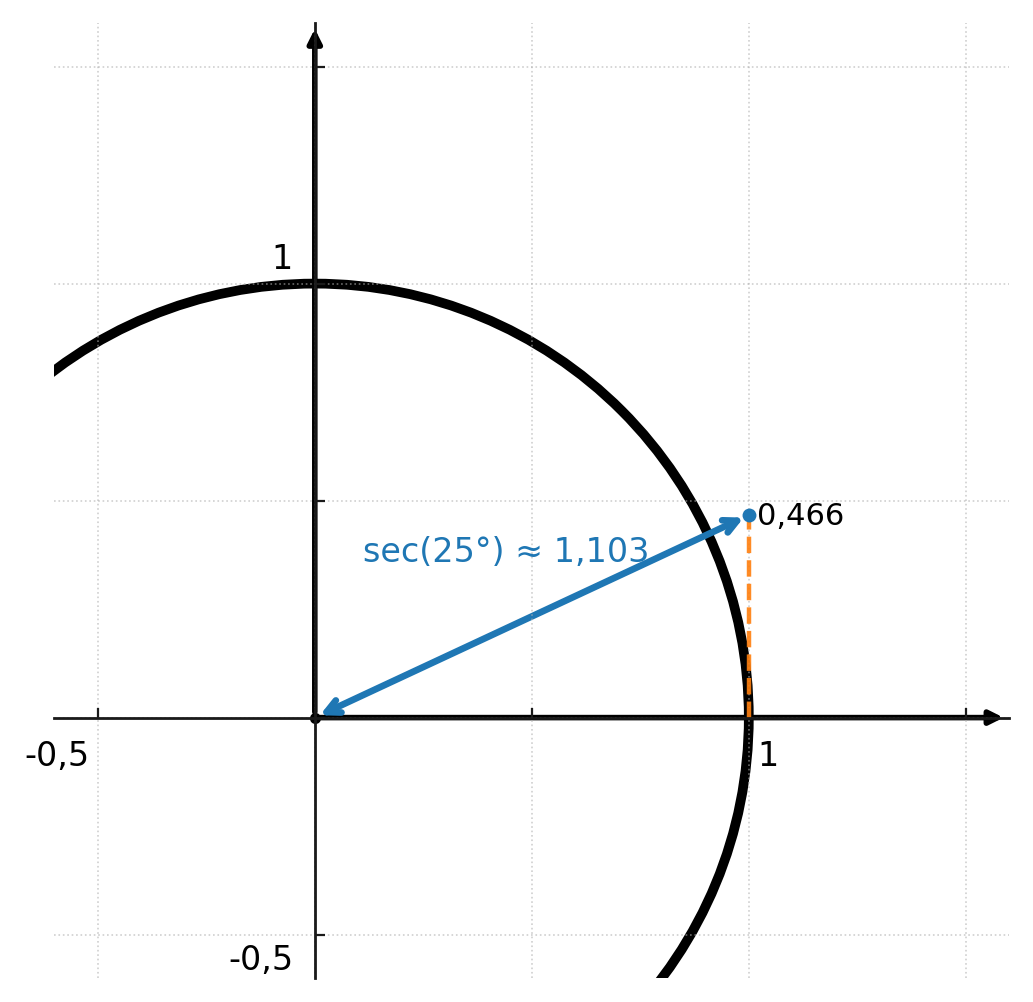
The distance from the center to the intersection point is the value of the function. The figure below shows that the tangent is 0.466 and the secant is 1.103.

 

 

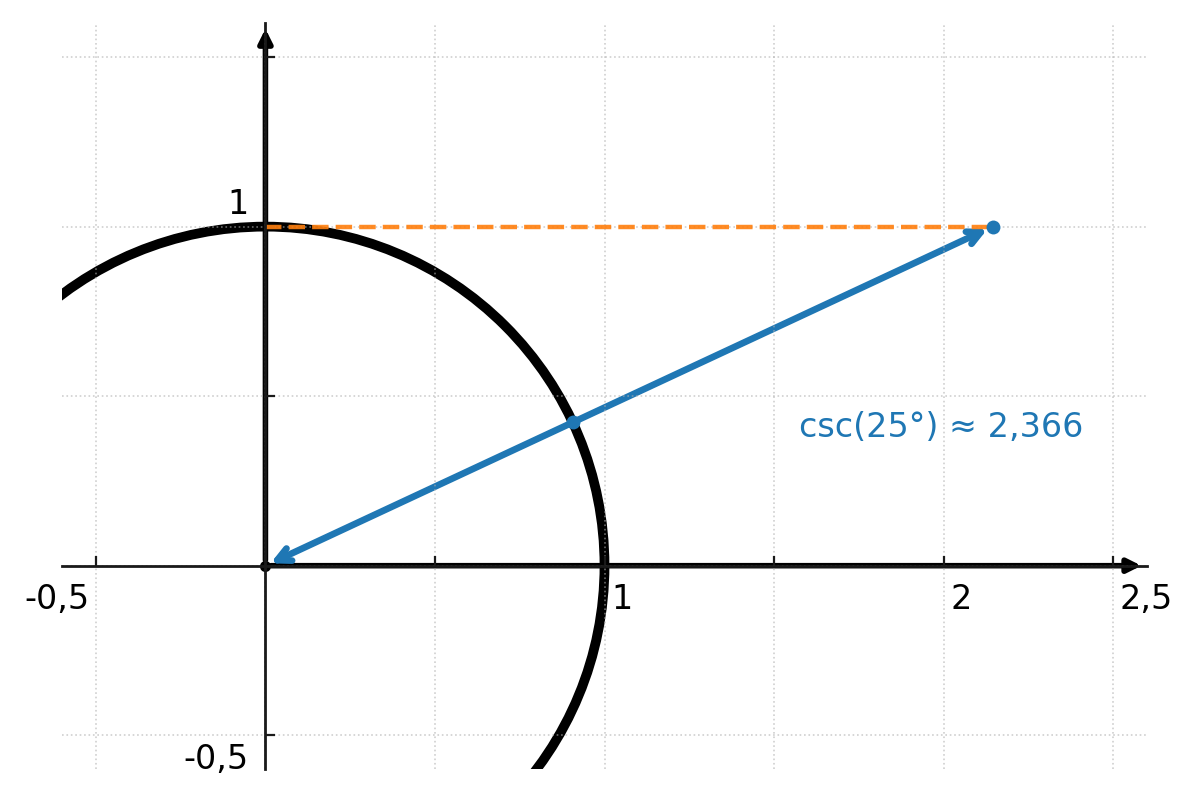
Here the cosecant is shown in the unit circle for the angle of 25 degrees, where the length from the center to the intersection point is 2.366

 

 

Application

Secant and cosecant are most useful in, for example, calculus and other advanced areas of mathematics, where they make certain calculations simpler.

In elementary geometry, one usually relies only on sine, cosine, and tangent.

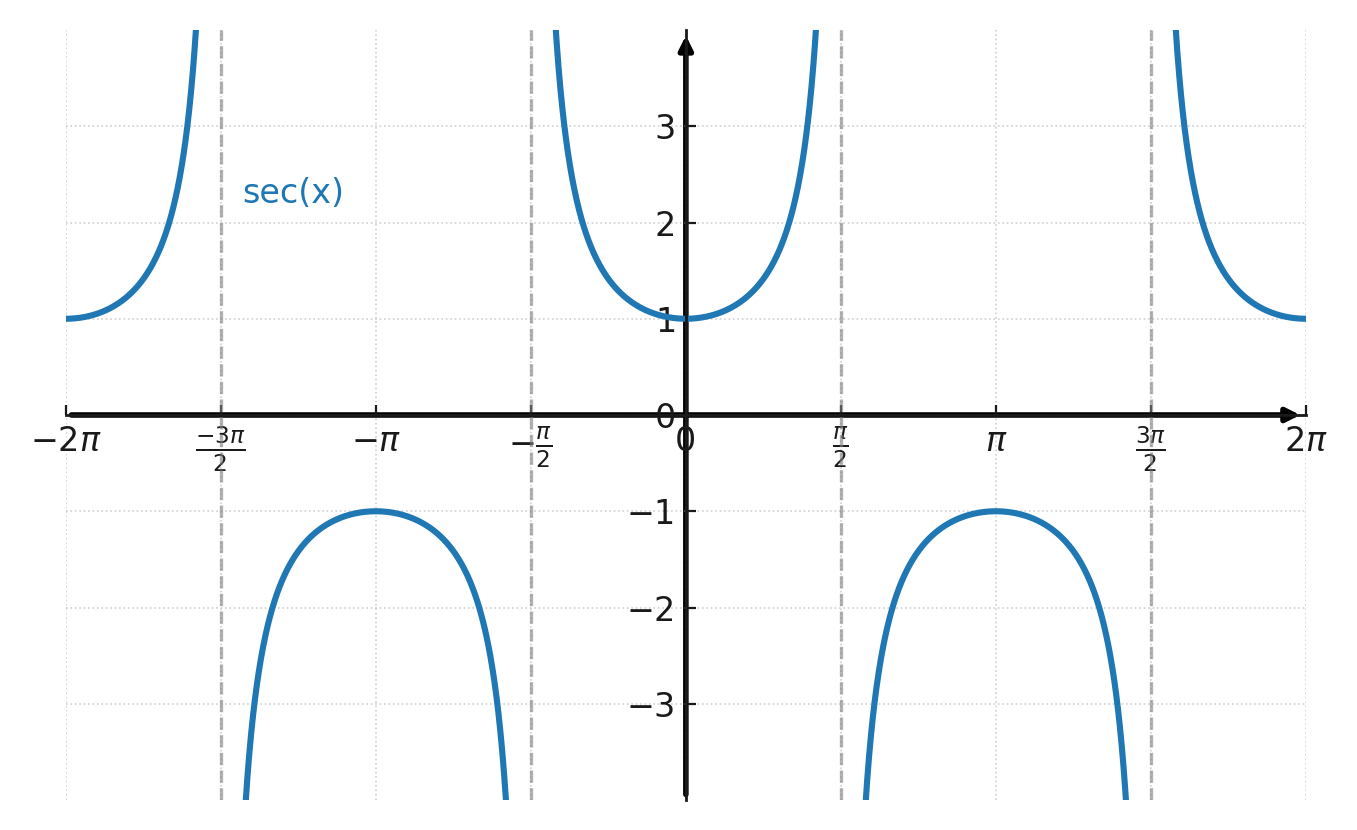
A quick look at the graphs of secant and cosecant explains why. The functions have vertical asymptotes, jump to very large values, and are not defined everywhere, unlike sine and cosine.

 

Graph of secant:

 

Graph of cosecant: