A parallelepiped is a three-dimensional geometric figure that has six faces, all of which are parallelograms. The figure can be regarded as a prism where the base is a parallelogram.

 

 

 

 

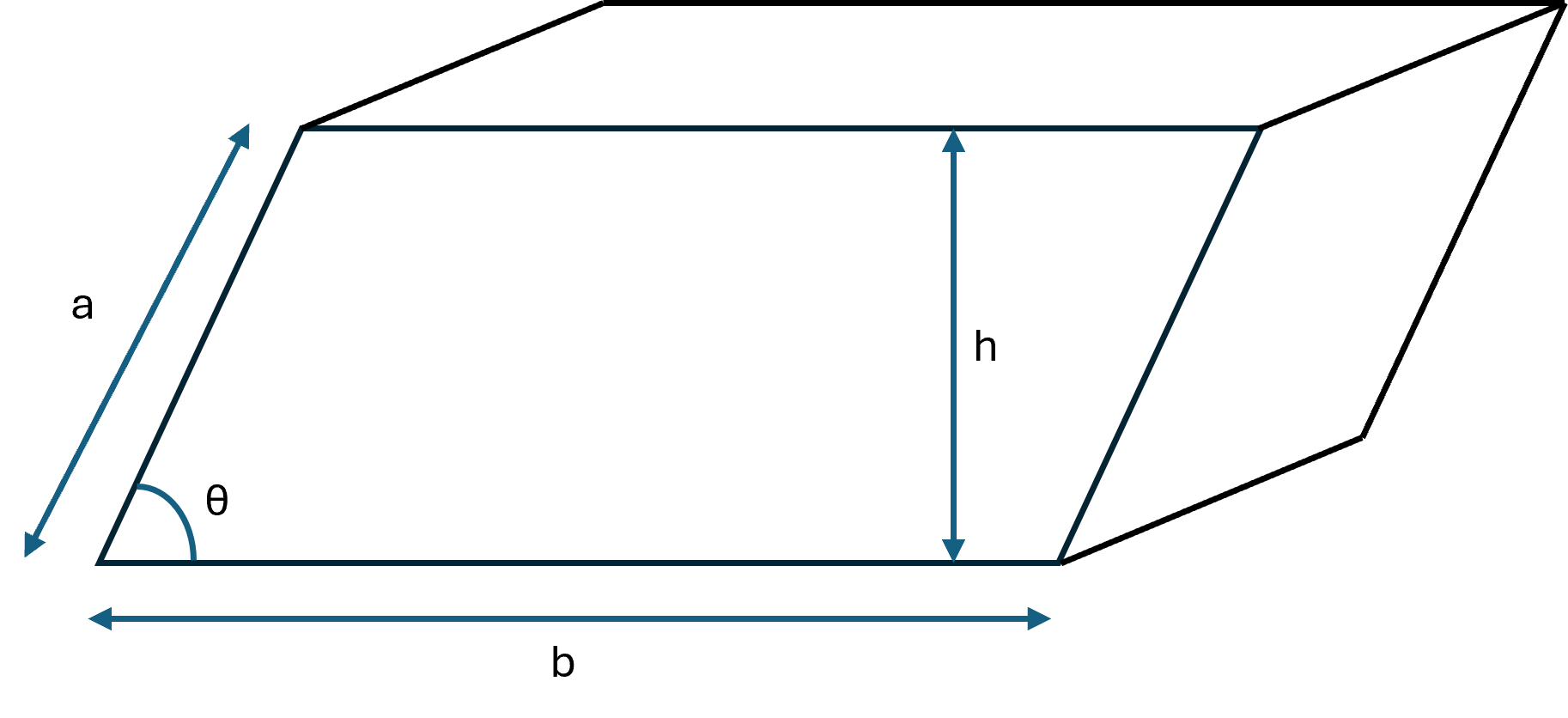
Volume

The volume of a parallelepiped is found by multiplying the area of the base by the height (the perpendicular distance between the base and the parallel surface):

 

$$ \large V = A_{base} \cdot h $$

 

The base is a parallelogram. If the side lengths are \( \large a \) and \( \large b \), and the angle between them is \( \large \theta \), the area is:

 

$$ \large A_{base} = a \cdot b \cdot \sin(\theta) $$

 

The volume therefore becomes:

 

$$ \large V = a \cdot b \cdot h \cdot \sin(\theta) $$

 

Example

Suppose a parallelepiped has a base where \( \large a = 6 \,\text{cm} \), \( \large b = 4 \,\text{cm} \), and the angle between them is \( \large 60^\circ \). The height is \( \large h = 10 \,\text{cm} \).

 

First, the base area is found:

 

$$ \large A_{base} = 6 \cdot 4 \cdot \sin(60^\circ) = 24 \cdot \tfrac{\sqrt{3}}{2} \approx 20.78 \,\text{cm}^2 $$

 

The volume is:

 

$$ \large V = 20.78 \cdot 10 \approx 207.8 \,\text{cm}^3 $$

 

Surface area

The surface area of a parallelepiped is found by summing the areas of the six parallelograms. There is no simple general formula as for the cube, since the result depends on the side lengths and angles.

 

In general, however, each pair of opposite faces is congruent, so one can calculate three different parallelogram areas and multiply by 2.