A prism is a three-dimensional figure that has two identical and parallel bases. The other faces are called lateral faces.

If the prism is right, the lateral faces are rectangles, and if it is oblique, they are parallelograms.

The end faces are called bases, and the distance between them is called the height.

 

 

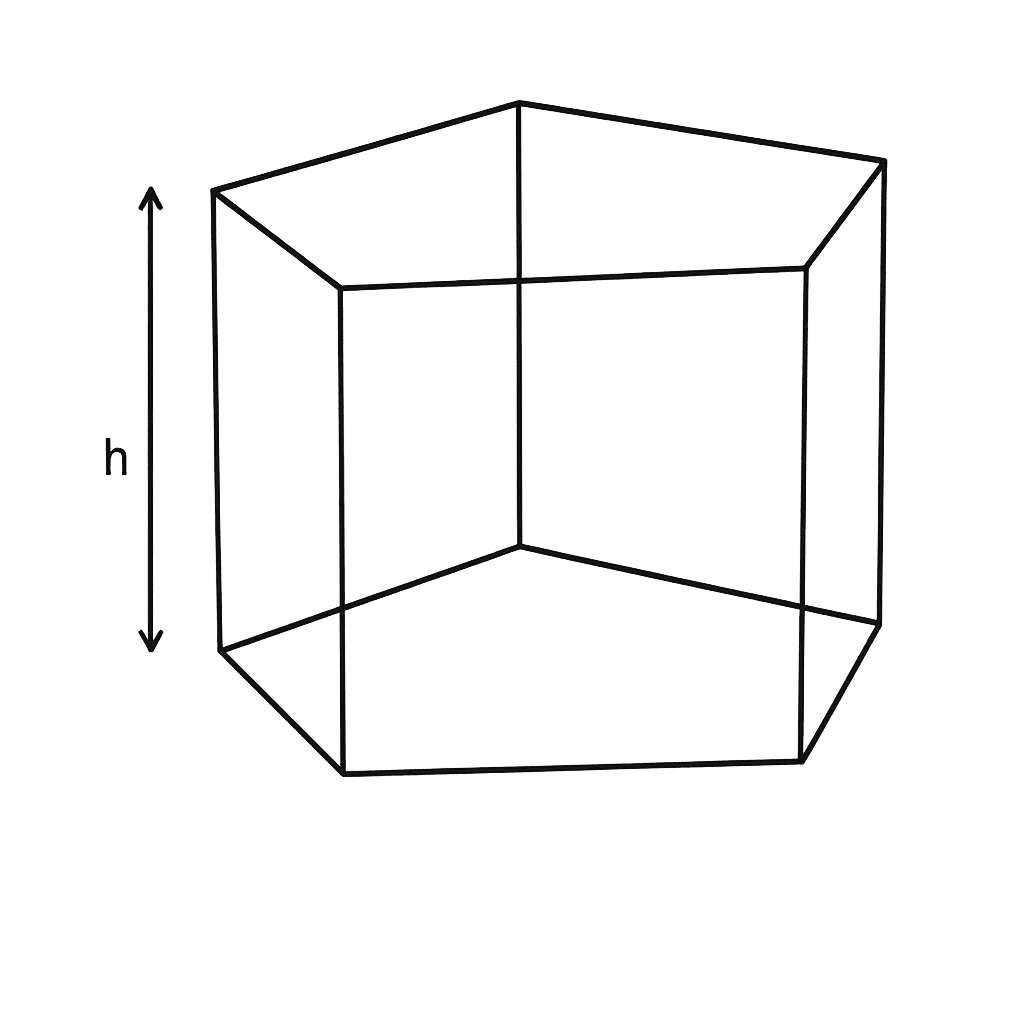
General properties

A prism can be right, when the lateral faces are perpendicular to the bases, or oblique, when they are slanted.

The bases can be any polygon, e.g. triangle, quadrilateral or hexagon. Therefore, there are many types of prisms.

 

Volume

The volume of a prism is found by taking the area of the base and multiplying it by the height.

In other words, one can say that the base is "stacked" upwards to obtain the whole size of the solid.

 

Surface area

The surface area of a prism consists of the two bases and all the lateral faces. It is therefore found by adding the area of both bases and then adding the area of all the lateral faces. The total area of the lateral faces can be calculated as the perimeter of the base multiplied by the height.

 

Examples of prisms

• Triangular prism – the simplest prism, where the bases are triangles.
• Quadrilateral prism – also called a box, if the bases are rectangles.
• Cube – a special quadrilateral prism where all edges are of equal length.
• Parallelepiped – a prism where the bases are parallelograms.
• Polygonal prisms – e.g. pentagonal and hexagonal prisms.

 

Prisms are often used in geometry, because they provide simple formulas for volume and surface area, and because many everyday objects have prism shapes.