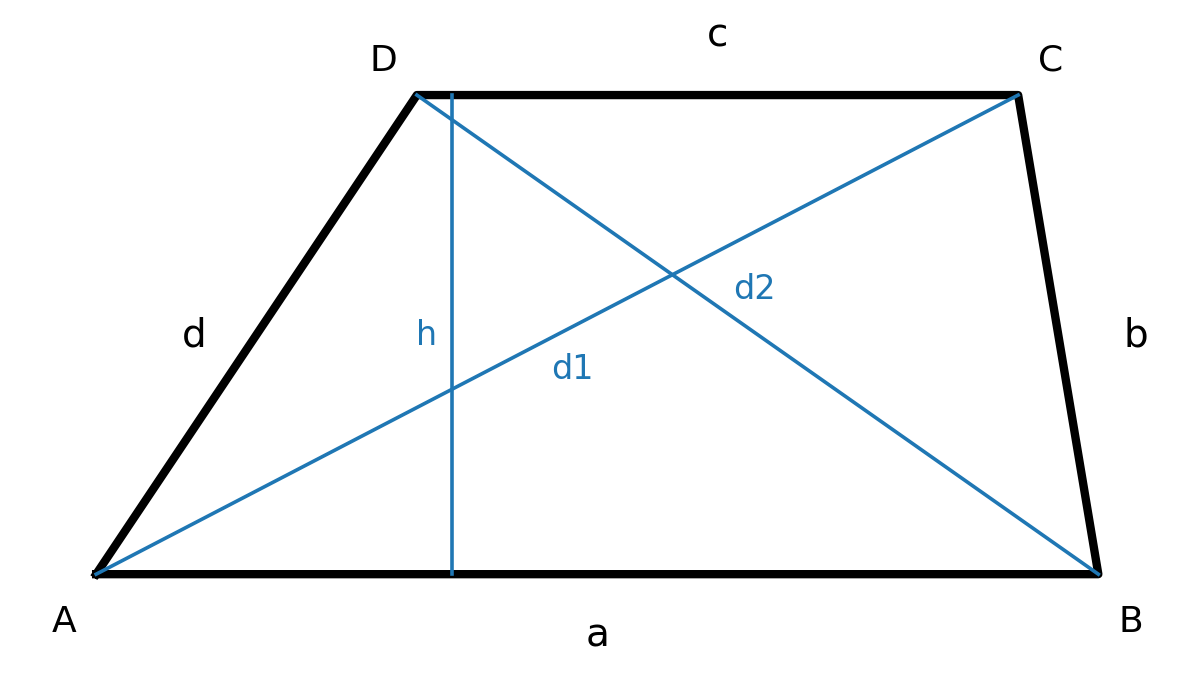
Trapezoid
A trapezoid is a quadrilateral where two of the sides are parallel. The parallel sides are called bases.
If the other two sides are also parallel, the figure is a parallelogram. The sides that are not parallel are called legs.
Variants
Isosceles trapezoid: \(b=d\). The base angles at each base are pairwise equal, and the diagonals are equal in length.
Right trapezoid: Two of the angles are right.
Properties
- The sum of the interior angles is 360°.
- Along each leg, \( \angle A + \angle D = 180^\circ \) and \( \angle B + \angle C = 180^\circ \) (parallelism).
- The midsegment (the line connecting the midpoints of the legs) has the length \( m=\tfrac{a+c}{2} \), and the area can be written \( A=m\cdot h \).
Area and perimeter
The standard formula for the area:
$$ \large A=\tfrac{h}{2}\,(a+c) $$
If the base angles at \(A\) and \(B\) are known, the lengths of the legs can be written as \( d=\tfrac{h}{\sin(\angle A)} \) and \( b=\tfrac{h}{\sin(\angle B)} \). Thus the perimeter becomes:
$$ \large P = (a+c) + h\!\left(\tfrac{1}{\sin(\angle A)}+\tfrac{1}{\sin(\angle B)}\right) $$
Area from four sides
If all four sides are known, the height and thus the area can be found without angles:
$$ \large A = \tfrac{1}{2}(a+c)\,\sqrt{\,b^2 - \Bigl(\tfrac{(a-c)^2 + b^2 - d^2}{2(a-c)}\Bigr)^2} $$
Here it is assumed that \(a \ne c\). For a parallelogram, take the limit \(a \to c\).
Diagonals
The diagonals are obtained with the cosine rule in the corresponding triangles:
$$ \large d_1 = \sqrt{a^2 + b^2 - 2ab\cos(\angle B)} $$
$$ \large d_1 = \sqrt{c^2 + d^2 - 2cd\cos(\angle D)} $$
$$ \large d_2 = \sqrt{a^2 + d^2 - 2ad\cos(\angle A)} $$
$$ \large d_2 = \sqrt{b^2 + c^2 - 2bc\cos(\angle C)} $$
In an isosceles trapezoid, \(d_1=d_2\).
Circumscribed circle
Only isosceles trapezoids can be inscribed in a circle. Equivalently, the opposite angle sums apply:
- \(\angle A + \angle C = 180^\circ\)
- \(\angle B + \angle D = 180^\circ\)
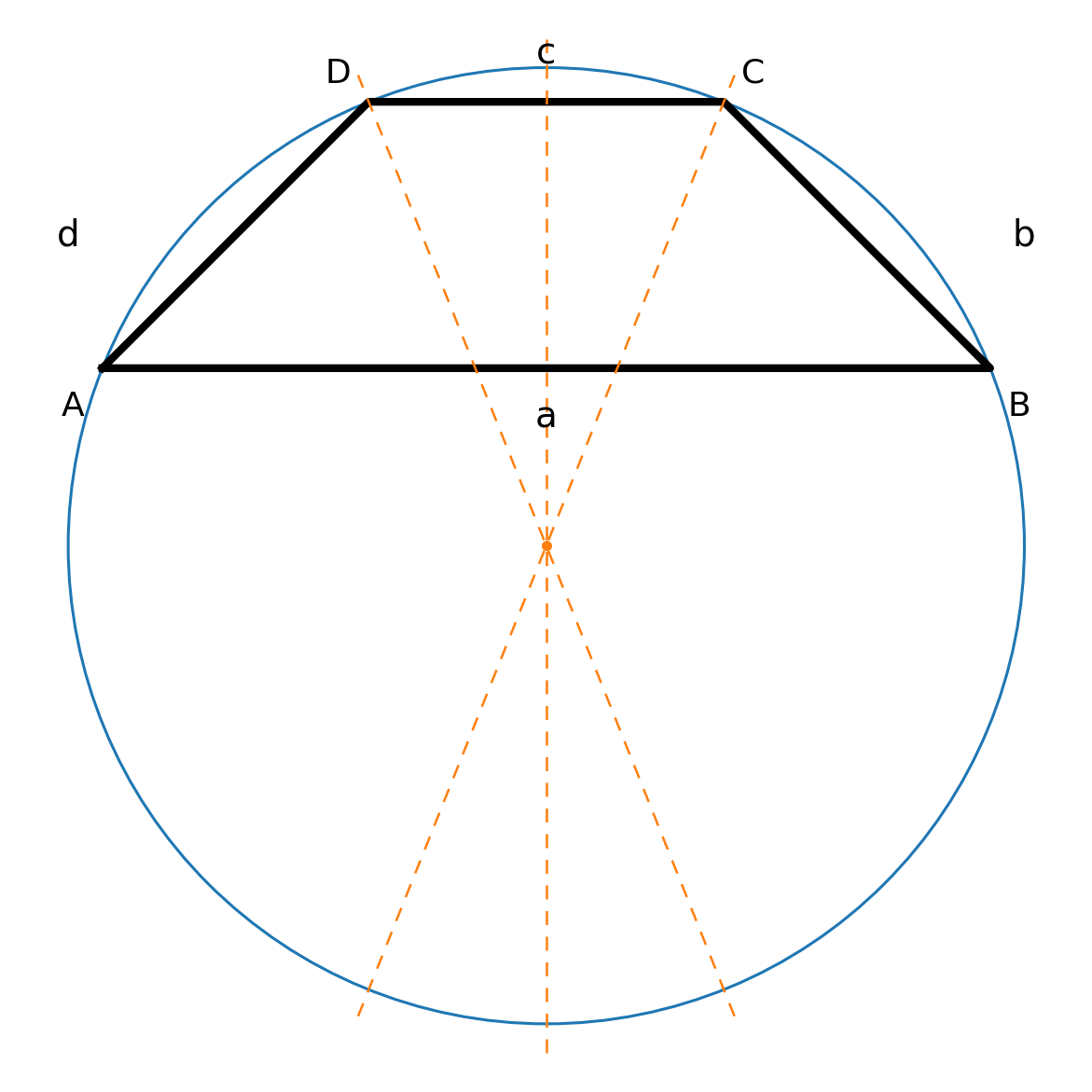
The center of the circle can be found by drawing angle bisectors from angle C and D, and optionally also the perpendicular bisector of sides a and c (the symmetry axis).
Note that for any trapezoid, \( \angle A + \angle D = 180^\circ \) and \( \angle B + \angle C = 180^\circ \) hold as a consequence of parallel lines. That alone does not make it cyclic.
Inscribed circle
A trapezoid has an inscribed circle, tangent to all four sides, if and only if:
$$ \large a + c = b + d $$
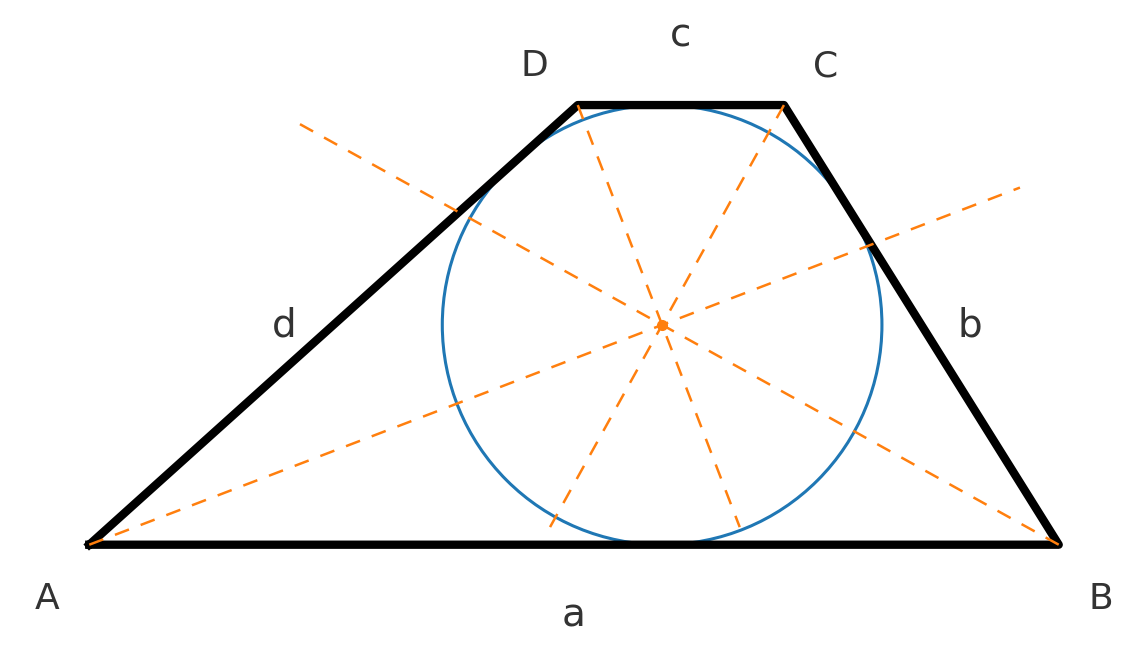
The center of the circle can be found by drawing angle bisectors from the four angles.
For tangential quadrilaterals, it also holds that \( A = r \cdot s \), where \( r \) is the inradius and \( s \) is the semiperimeter.
Applications
- Dividing into two right triangles plus a rectangle makes constructions and trigonometric calculations manageable.
- The trapezoidal rule is used for numerical approximation of integrals.